Nullstelle lineare Funktion
Du fragst dich, wie du die Nullstelle einer linearen Funktion berechnest? In diesem Artikel und im Video zeigen wir dir Schritt für Schritt, wie das geht, und geben dir praktische Beispiele an die Hand!
Inhaltsübersicht
Nullstelle lineare Funktion – Einfach erklärt
Eine Nullstelle einer linearen Funktion ist der Punkt, an dem die Gerade die x-Achse schneidet.
Um die Nullstelle zu berechnen, setzt du den Funktionswert f(x) gleich Null. Dann löst du die Gleichung nach x auf. Bei der Funktion f(x) = 2x + 3 setzt du also zum Beispiel
2x + 3 = 0.
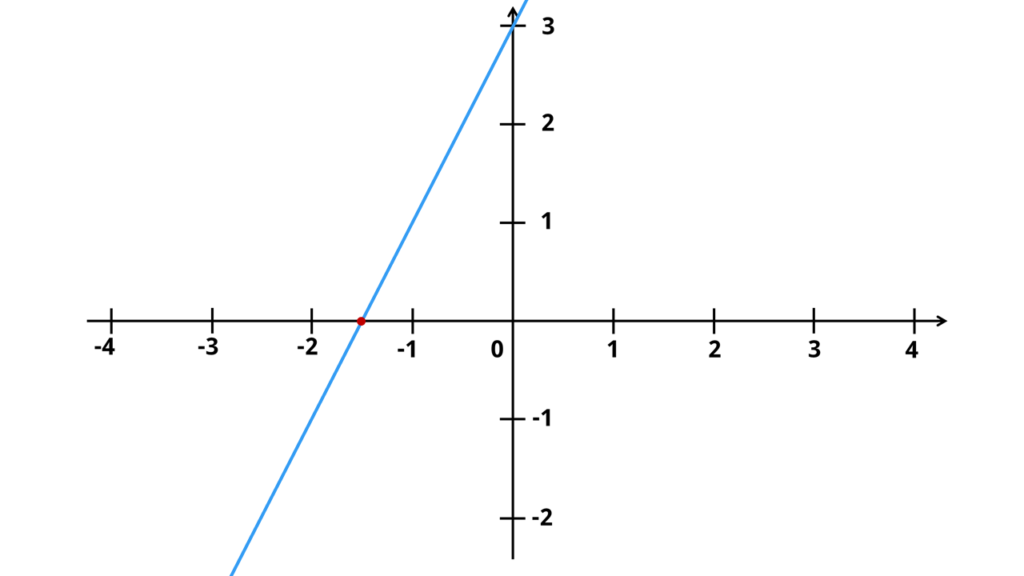
Dann subtrahierst du zuerst 3 von beiden Seiten der Gleichung. Zuletzt teilst du das Ergebnis durch 2. Damit bekommst du die Nullstelle bei x = -1,5.
Du kannst die Nullstelle auch an dem Graph der Funktion ablesen. Suche dafür den Punkt, wo die Funktion die x-Achse schneidet. Das ist deine Nullstelle.
Nullstelle einer linearen Funktion berechnen
Mit diesen vier Schritten kannst du die Nullstellen von jeder linearen Funktion berechnen:
-
Gleichung gleich Null setzen:
Du hast zum Beispiel die Funktion f(x) = 5x – 10. Setze sie gleich Null:
5x – 10 = 0
-
Konstante auf die andere Seite bringen:
Addiere 10 auf beiden Seiten:
5x – 10 = 0 | +10
5x = 10
-
Durch den Koeffizienten teilen:
Teile beide Seiten durch 5:
5x = 10 | :5
x = 2
Die Nullstelle der Funktion f(x) = 5x – 10 liegt also bei x = 2.
Diese Schritte bleiben immer gleich, auch wenn die Gleichungen der Funktion etwas komplizierter werden.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Nullstelle einer linearen Funktion — Beispiele
Schauen wir uns verschiedene Beispiele an, um die Schritte noch besser zu verstehen:
Einfaches Beispiel: Du hast die Funktion f(x) = 4x – 8.
- Setze 4x – 8 = 0.
- Addiere 8 auf beiden Seiten: 4x = 8.
- Teile dann durch 4: x = 2.
Die Nullstelle ist also bei x = 2.
Mittelschweres Beispiel: Sieh dir die Funktion f(x) = -3x + 6 an.
- Setze -3x + 6 = 0.
- Subtrahiere 6: -3x = -6.
- Teile durch -3: x = 2.
Auch hier ist die Nullstelle bei x = 2.
Komplexeres Beispiel: Nun hast du die Funktion f(x) = 0,5x – 7,5.
- Setze 0,5x – 7,5 = 0.
- Addiere 7,5: 0,5x = 7,5.
- Teile durch 0,5: x = 15.
Die Nullstelle liegt also bei x = 15.
Lineare Funktionen ohne Nullstelle
Nicht jede lineare Funktion hat eine Nullstelle. Konstante Funktionen wie f(x) = 3 haben zum Beispiel keine Nullstelle. Diese Funktionen verlaufen parallel zur x-Achse und haben überall den gleichen y-Wert. Sie schneiden die x-Achse also nie.
Wichtig: Es gibt eine Ausnahme. Die Konstante Funktion f(x) = 0 liegt genau auf der x-Achse. Hier ist bei jedem x eine Nullstelle.
Nullstelle lineare Funktion — häufigste Fragen
(ausklappen)
Nullstelle lineare Funktion — häufigste Fragen
(ausklappen)-
Wie berechne ich die Nullstelle, wenn vor x Klammern stehen?Die Nullstelle berechnest du auch mit Klammern, indem du zuerst
 setzt und dann die Klammern auflöst oder sinnvoll ausmultiplizierst. Danach fasst du gleichartige Terme zusammen und löst die lineare Gleichung nach
setzt und dann die Klammern auflöst oder sinnvoll ausmultiplizierst. Danach fasst du gleichartige Terme zusammen und löst die lineare Gleichung nach  . Zum Beispiel wird aus
. Zum Beispiel wird aus  nach dem Ausmultiplizieren
nach dem Ausmultiplizieren  und damit
und damit  .
.
-
Welche Fehler passieren oft beim Umformen zur Nullstelle?Häufige Fehler beim Umformen zur Nullstelle sind Vorzeichenfehler beim „rüberbringen“, falsches Ausmultiplizieren von Klammern und das Vergessen, beide Seiten gleich zu behandeln. Zum Beispiel ist bei
 korrekt
korrekt  und damit
und damit  ; falsch wäre
; falsch wäre  , weil das Minus nicht auf beide Klammerterme verteilt wurde.
, weil das Minus nicht auf beide Klammerterme verteilt wurde.
-
Warum ändert sich das Vorzeichen, wenn ich durch eine negative Zahl teile?Das Vorzeichen ändert sich, weil das Teilen durch eine negative Zahl dasselbe ist wie das Multiplizieren mit einer negativen Zahl und das kehrt das Vorzeichen um. Deshalb wird aus
 nach dem Teilen durch
nach dem Teilen durch  der Wert
der Wert  , weil
, weil  .
.
-
Wie prüfe ich schnell, ob meine Nullstelle stimmt?Eine Nullstelle stimmt, wenn beim Einsetzen in die Funktion wirklich
 herauskommt. Setze dazu deinen gefundenen
herauskommt. Setze dazu deinen gefundenen  -Wert in den Funktionsterm ein und rechne nach. Zum Beispiel ist
-Wert in den Funktionsterm ein und rechne nach. Zum Beispiel ist  eine Nullstelle von
eine Nullstelle von  , weil
, weil  .
.
-
Wann hat eine lineare Funktion unendlich viele Nullstellen?Eine lineare Funktion hat unendlich viele Nullstellen genau dann, wenn sie überall den Wert 0 hat, also
 für jedes
für jedes  . Das ist die konstante Nullfunktion, deren Graph auf der x-Achse liegt. Dann ist jeder x-Wert eine Nullstelle, weil immer
. Das ist die konstante Nullfunktion, deren Graph auf der x-Achse liegt. Dann ist jeder x-Wert eine Nullstelle, weil immer  gilt.
gilt.
Nullstellen berechnen quadratische Funktionen
Im nächsten Video erfährst du alles über die Nullstellen quadratischer Funktionen. Lerne, wie du sie berechnest und welche Besonderheiten es gibt.