Polynomdivision Aufgaben
Dieser Beitrag ergänzt unseren Artikel zur Polynomdivision um eine Vielzahl an Aufgaben. Zu jeder Aufgabe gibt es auch eine Lösung. Zusätzlich findest du ein ausführliches Video mit Polynomdivision Aufgaben.
Inhaltsübersicht
Lösung zu Aufgabe 1
Der Term mit dem höchsten Exponenten im ersten Polynom
ist  . Um mit dem Polynom
. Um mit dem Polynom  ein
ein  zu erhalten, müssen wir es mit
zu erhalten, müssen wir es mit  multiplizieren, also
multiplizieren, also

Wir ergänzen zu  den nächsten Term
den nächsten Term  und ziehen davon das Ergebnis der vorherigen Multiplikation ab.
und ziehen davon das Ergebnis der vorherigen Multiplikation ab.

Zu  ergänzen wir den nächsten Teil des ersten Polynoms
ergänzen wir den nächsten Teil des ersten Polynoms  und erhalten
und erhalten

Der Term mit dem höchsten Exponenten ist jetzt  . Wir müssen daher das zweite Polynom mit
. Wir müssen daher das zweite Polynom mit  multiplizieren, also
multiplizieren, also

Nun subtrahieren wir wieder

Damit sind wir ans Ende der Polynomdivision gelangt.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Polynomdivision Aufgabe 2
Berechne die folgende Polynomdivision
 .
.
Lösung zu Aufgabe 2
Der Term mit dem höchsten Exponenten im ersten Polynom
ist  . Um diesen mit dem zweiten Polynom
. Um diesen mit dem zweiten Polynom  verschwinden zu lassen, müssen wir das zweite Polynom mit
verschwinden zu lassen, müssen wir das zweite Polynom mit  multiplizieren, also
multiplizieren, also

Wir ergänzen zu  den nächsten Term
den nächsten Term  und ziehen davon das Ergebnis der vorherigen Multiplikation ab
und ziehen davon das Ergebnis der vorherigen Multiplikation ab

Zu  ergänzen wir den nächsten Teil des ersten Polynoms
ergänzen wir den nächsten Teil des ersten Polynoms  und erhalten
und erhalten

Der Term mit dem höchsten Exponenten ist jetzt  . Wir müssen daher das zweite Polynom mit
. Wir müssen daher das zweite Polynom mit  multiplizieren, also
multiplizieren, also

Nun subtrahieren wir wieder

Damit sind wir ans Ende der Polynomdivision gelangt.
Lösung zu Aufgabe 3
Der Term mit dem höchsten Exponenten im ersten Polynom
ist  . Um diesen mit dem zweiten Polynom
. Um diesen mit dem zweiten Polynom  verschwinden zu lassen, müssen wir das zweite Polynom mit
verschwinden zu lassen, müssen wir das zweite Polynom mit  multiplizieren, also
multiplizieren, also

Wir ergänzen zu  den nächsten Term
den nächsten Term  und ziehen davon das Ergebnis der vorherigen Multiplikation ab
und ziehen davon das Ergebnis der vorherigen Multiplikation ab
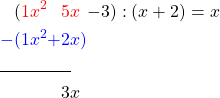
Zu  ergänzen wir den nächsten Teil des ersten Polynoms
ergänzen wir den nächsten Teil des ersten Polynoms  und erhalten
und erhalten

Der Term mit dem höchsten Exponenten ist jetzt  . Wir müssen daher das zweite Polynom mit
. Wir müssen daher das zweite Polynom mit  multiplizieren, also
multiplizieren, also

Nun subtrahieren wir wieder

Damit sind wir ans Ende der Polynomdivision gelangt.
Polynomdivision Aufgabe 4
Berechne die folgende Polynomdivision
 .
.
Lösung zu Aufgabe 4
Der Term mit dem höchsten Exponenten im ersten Polynom
ist  . Um diesen mit dem zweiten Polynom
. Um diesen mit dem zweiten Polynom  verschwinden zu lassen, müssen wir das zweite Polynom mit
verschwinden zu lassen, müssen wir das zweite Polynom mit  multiplizieren, also
multiplizieren, also

Wir ergänzen zu  den nächsten Term
den nächsten Term  und ziehen davon das Ergebnis der vorherigen Multiplikation ab
und ziehen davon das Ergebnis der vorherigen Multiplikation ab

Zu  ergänzen wir den nächsten Teil des ersten Polynoms
ergänzen wir den nächsten Teil des ersten Polynoms  und erhalten
und erhalten
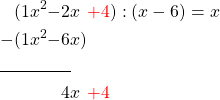
Der Term mit dem höchsten Exponenten ist jetzt  . Wir müssen daher das zweite Polynom mit
. Wir müssen daher das zweite Polynom mit  multiplizieren, also
multiplizieren, also

Nun subtrahieren wir wieder

Damit sind wir ans Ende der Polynomdivision gelangt.
Polynomdivision Aufgabe 5
Du hast das folgende Polynom gegeben
 .
.
Dieses Polynom besitzt die Nullstelle  . Berechne die fehlenden Nullstellen
. Berechne die fehlenden Nullstellen  und
und  .
.
Lösung zu Aufgabe 5
Im ersten Schritt berechnen wir die Polynomdivision
 .
.
Das zweite Polynom lautet  und nicht
und nicht  , da die gegebene Nullstelle ein negatives Vorzeichen besitzt. Das Ergebnis der Polynomdivision lautet:
, da die gegebene Nullstelle ein negatives Vorzeichen besitzt. Das Ergebnis der Polynomdivision lautet:

Wir haben durch die Polynomdivision ein neues Polynom erhalten
 .
.
An dieser Stelle solltest du erkennen, dass durch die Polynomdivision der höchste Exponent nicht mehr 3, sondern 2 ist. Du kannst also die dir bekannten Methoden zum Bestimmen der Nullstellen verwenden, wie die Mitternachtsformel oder die pq-Formel . Dadurch erhältst du hier die zwei weiteren Nullstellen
 und
und  .
.
Zusatz: Linearfaktoren und Probe
Zusätzlich zum Berechnen der Nullstellen, könntest du durch die Aufgabe darum gebeten werden, das Polynom  in Linearfaktoren zu zerlegen und eine Probe durchzuführen. Wir zeigen dir, wie du das in diesem Fall machst.
in Linearfaktoren zu zerlegen und eine Probe durchzuführen. Wir zeigen dir, wie du das in diesem Fall machst.
Wir haben die folgenden drei Nullstellen
 ,
,  und
und  .
.
Die Zerlegung von  in Linearfaktoren sieht dann so aus
in Linearfaktoren sieht dann so aus
 .
.
Du verwendest also das Rezept „x MINUS Nullstelle“. Wichtig ist das „MINUS“. Dadurch dreht sich das Vorzeichen in der Zerlegung um.
Für die Probe multiplizierst du schrittweise die Klammern aus
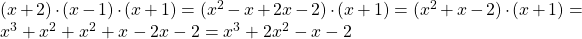 .
.
Das Ergebnis am Ende ist gerade das Polynom  .
.
Polynomdivision Aufgabe 6
Du hast das folgende Polynom gegeben
 .
.
Dieses Polynom besitzt die Nullstelle  . Berechne die fehlenden Nullstellen
. Berechne die fehlenden Nullstellen  und
und  .
.
Lösung zu Aufgabe 6
Im ersten Schritt berechnen wir die Polynomdivision
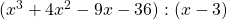 .
.
Das zweite Polynom lautet 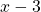 und nicht
und nicht  , da die gegebene Nullstelle ein positives Vorzeichen besitzt. Das Ergebnis der Polynomdivision lautet:
, da die gegebene Nullstelle ein positives Vorzeichen besitzt. Das Ergebnis der Polynomdivision lautet:

Die Polynomdivision liefert uns ein neues Polynom
 .
.
Dieses besitzt als größten Exponenten 2. Um die weiteren Nullstellen zu berechnen, kannst du daher Methoden wie die Mitternachtsformel oder pq-Formel verwenden. Die zwei weiteren Nullstellen lauten dann
 und
und  .
.
Zusammenfassung
Die Polynomdivision hilft dir dabei, verschiedenste Aufgaben zu lösen. Häufig brauchst du sie,
- um Polynome auf eine quadratische Funktion zu reduzieren,
- um Nullstellen berechnen zu können,
- um die Linearfaktorzerlegung zu bilden.
Schau dir gleich unsere Videos zu den einzelnen Themen an, um mehr darüber zu erfahren!
 .
. .
.