Wertebereich
Du willst wissen, was der Wertebereich ist und wie du den Wertebereich bestimmen kannst? Hier erfährst du alles, was du wissen musst!
Inhaltsübersicht
Wertebereich einfach erklärt
Bei der Kurvendiskussion in Mathe gehört es dazu, den Wertebereich zu bestimmen! Doch was ist der Wertebereich eigentlich?
Den Wertebereich bekommst du, wenn du alle möglichen x-Werte aus dem Definitionsbereich in deine Funktion f(x) einsetzt. Die Summe der Ergebnisse ist der Wertebereich — also alle Zahlen, die deine Funktion auf der y-Achse (senkrechte Achse) annehmen kann.
Hast du eine Abbildung des Graphen, kannst du den Wertebereich einfach ablesen. Dafür schaust du dir an, welche y-Werte (senkrechte Achse) deine Funktion insgesamt oder in einem bestimmten Intervall annehmen kann.
Wie du rechnerisch den Wertebereich bei verschiedenen Funktionen bestimmen kannst, schauen wir uns jetzt an. Denn für jede Funktion gibt es ein Vorgehen, das du dir einfach merken kannst!
Wertebereich bestimmen — konstante Funktion
Eine konstante Funktion hat die Form f(x) = c, zum Beispiel f(x) = 3. Die Funktion hat immer denselben y-Wert, nämlich die Konstante c! Du musst also nicht rechnen, sondern kannst die Wertemenge einfach ablesen: W = {3}
Der Wertebereich einer konstanten Funktion ist also immer die Konstante selbst. Sie ist der einzige Wert, den die y-Achse annimmt. Hier ist das: W = {3}.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Lineare Funktion — Wertebereich bestimmen
Bei linearen Funktionen ist der Wertebereich ganz einfach zu bestimmen, denn er ist immer W = R.
Egal, welche lineare Funktion du nämlich hast, sie kann immer alle Werte auf der y-Achse annehmen. Schau dir das Beispiel f(x) = 2x an:
Die Funktion kann jede reelle Zahl auf der y-Achse annehmen, deshalb ist W = R.
Quadratische Funktion — Wertebereich bestimmen
Quadratische Funktionen haben die Form von Parabeln . Wenn sie nach oben geöffnet sind, haben sie immer einen Tiefpunkt. Und wenn sie nach unten geöffnet sind, haben sie immer einen Hochpunkt. In die andere Richtung gehen sie bis ins Unendliche.
Für den Wertebereich kannst du dir merken:
- bei einer Parabel mit Hochpunkt H ist die Wertemenge W = ]−∞; H]
- bei einer Parabel mit Tiefpunkt T ist die Wertemenge W = [T; +∞[
Um den Wertebereich rechnerisch zu bestimmen, kannst du also einfach den Extrempunkt der quadratischen Funktion berechnen. Dann weißt du, welchen y-Wert deine Funktion höchstens annehmen kann.
Funktionen höheren Grades — Wertebereich bestimmen
Den Wertebereich von Funktionen höheren Grades zu bestimmen, ist gar nicht schwer!
- Bei Funktionen mit ungeradem Exponenten, z. B. f(x) = (x-3)3 +1 gilt immer W = R. Wie bei linearen Funktionen kann die Funktion jeden y-Wert annehmen.
- Bei Funktionen mit geradem Exponenten, z. B. g(x) = (x+2)4 +2 gehst du vor wie bei den quadratischen Funktionen: Ermittle den Hoch- oder Tiefpunkt, um den höchsten oder niedrigsten y-Wert herauszufinden. In die andere Richtung geht die Funktion bis ins Unendliche.
Tipp! Hast du nur die Funktion gegeben, dann stell dir vor, wie der Graph aussieht. Das hilft dir dabei, dir den Wertebereich vorzustellen.
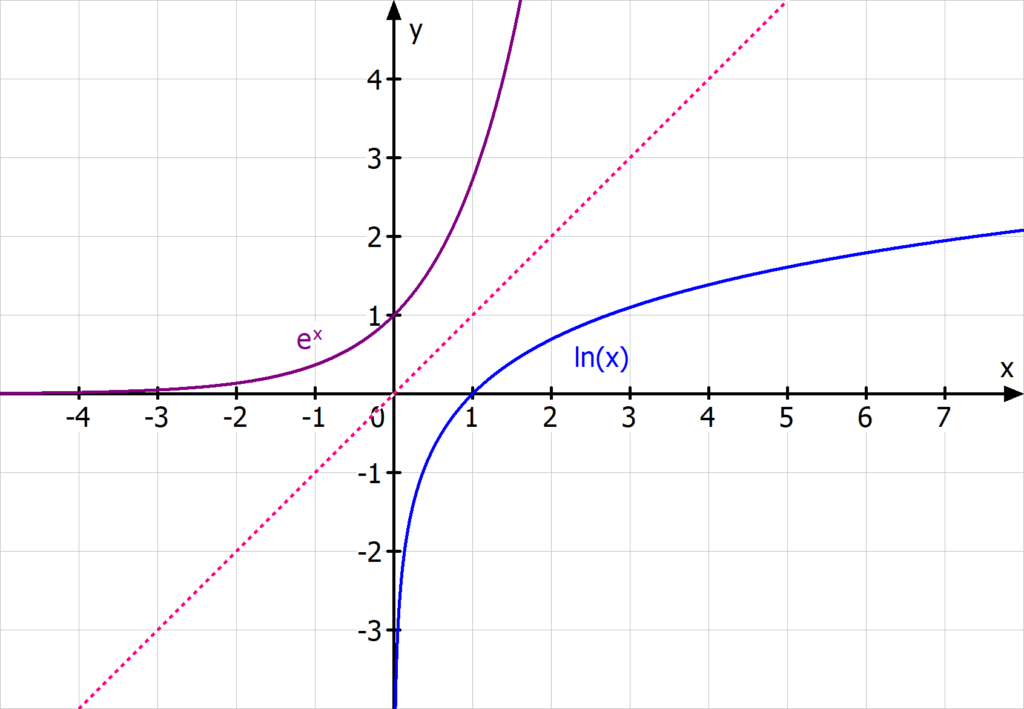
Wertebereich e-Funktion und ln-Funktion
Die e-Funktion und die ln-Funktion hängen eng miteinander zusammen: Um den Wertebereich der einen Funktion zu bestimmen, schaust du dir einfach den Definitionsbereich der anderen Funktion an.
- Der Definitionsbereich der e-Funktion enthält alle reellen Zahlen D = R. Der Wertebereich der e-Funktion besteht nur aus den positiven reellen Zahlen W = R+.
- Der Definitionsbereich der ln-Funktion enthält nur alle positiven reellen Zahlen D = R+. Der Wertebereich der ln-Funktion besteht aus allen reellen Zahlen W = R.
Tipp! Merke dir für die e-Funktion und ln-Funktion einfach, dass du Definitions- und Wertebereich vertauschen kannst. Der Wertebereich der e-Funktion ist der Definitionsbereich der ln-Funktion — und andersrum! So musst du nie etwas berechnen!
Wertebereich bestimmen — trigonometrische Funktionen
Auch der Wertebereich von trigonometrischen Funktionen ist ganz einfach zu bestimmen! Im Normalfall nehmen die Sinus – und Cosinus -Funktion nämlich nur die y-Werte von -1 bis 1 an.
Der Wertebereich ist also W = [-1; 1].
Manchmal sind die Funktionen jedoch gestreckt oder gestaucht. Dann nimmst du einfach den Faktor vor der Funktion mit in den Wertebereich. Zum Beispiel hat die Funktion f(x) = 2 sin(x) den Wertebereich W = [2 • (-1); 2 • 1], also W = [-2; 2].
Ist die trigonometrische Funktion an der y-Achse verschoben, verändert sich auch der Wertebereich. Dann nimmst du die Verschiebung einfach zu deinem Wertebereich dazu. Die Funktion g(x) = sin (x) + 3 hat zum Beispiel den Wertebereich W = [-1+3; 1+3], also W = [2; 4].
Die Tangens-Funktion kann immer alle y-Werte annehmen und hat deshalb den Wertebereich W = R.
Jetzt kannst du die Wertemenge von trigonometrischen Funktionen bestimmen! Wie das bei gebrochenrationalen Funktionen geht, schauen wir uns jetzt an!
Gebrochenrationale Funktion — Wertebereich bestimmen
Eine gebrochenrationale Funktion hat ein x im Nenner und weist deshalb Definitionslücken auf. Darum ist es nicht ganz so einfach, den Wertebereich der Funktion herauszufinden. Doch du kannst einfach Schritt für Schritt vorgehen!
1. Schritt: Finde die Definitionslücken der Funktion heraus.
Schaue also, was du nicht in die Funktion einsetzen darfst. Im Nenner darf zum Beispiel nie 0 stehen. Mit dem Definitionsbereich kannst du jetzt weiter den Wertebereich bestimmen.
2. Schritt: Bestimme alle Extrempunkte der Funktion.
Das machst du, indem du die Nullstellen der ersten Ableitung f'(x) bestimmst.
3. Schritt: Untersuche die Ränder des Definitionsbereichs.
Schau dir also für jedes Intervall an, in welche Richtung sich die Funktion bewegt. Dazu kannst du entweder eine Grenzwertbetrachtung
durchführen oder den Limes bestimmen.
4. Schritt: Bestimme den Wertebereich der Funktion.
Mit deinen berechneten Informationen kannst du nun für jedes Intervall den Wertebereich bestimmen. So hast du am Ende den Wertebereich der gesamten Funktion!
Wertebereich in einem Intervall
Manchmal musst du nicht den gesamten Wertebereich einer Funktion bestimmen, sondern nur den Wertebereich für ein bestimmtes Intervall.
Schau dir zum Beispiel diese Funktion an. Du willst den Wertebereich im Intervall [3; 5] bestimmen. Dazu schaust du dir einfach an, welche y-Werte die Funktion nur in diesem Intervall annimmt. Hier ist das W = [1; 5].
Nun kannst du für jede Funktion den Wertebereich bestimmen!
Wertebereich Definition — kurz & knapp
Das solltest du zum Definitionsbereich und Wertebereich wissen:
- Der Wertebereich sagt dir, welche y-Werte eine Funktion annehmen kann.
- Er beantwortet dir die Frage: Welche Zahlen können rauskommen, wenn ich x-Werte aus dem Definitionsbereich einsetze?
- Bei linearen Funktionen besteht der Wertebereich aus allen reellen Zahlen .
- Den Wertebereich musst du immer am Beginn einer Kurvendiskussion angeben.
Wertebereich — häufigste Fragen
-
Was versteht man unter Wertebereich?
Der Wertebereich gibt dir alle Werte an, die als Ergebnis (y-Wert) herauskommen können, wenn du alle erlaubten x-Werte in die Funktion einsetzt. Die erlaubten x-Werte gibt dir der Definitionsbereich an.
-
Wie kann man den Wertebereich angeben?
Um den Wertebereich zu bestimmen, darfst du nur x-Werte aus der Definitionsmenge in die Funktion einsetzen. Wenn du den Wertebereich eines bestimmten Intervalls betrachtest, dann setzt du nur die x-Werte aus diesem Intervall ein, zum Beispiel von -5 bis 5.
Extrempunkte berechnen
Die Bestimmung des Wertebereichs ist oft Teil einer Kurvendiskussion, da du dazu häufig die Extrempunkte einer Funktion berechnen musst. In unserem Video dazu erklären wir dir genau, was Extrempunkte sind und wie du sie berechnest. Schau es dir an!