Video anzeigen

Winkelfunktionen

Wichtige Inhalte in diesem Video

Sinus Cosinus und Tangens für alle Winkel

Du willst wissen, was Winkelfunktionen sind und wie du rechtwinklige Dreiecke mit Winkelfunktionen berechnen kannst? Das alles erfährst du hier im Artikel und in unserem Video ! %Alles bis einschließlich "Aufgaben: Winkelfunktionen Formeln" muss Korrektur gelesen werden

Inhaltsübersicht

Winkelfunktionen einfach erklärt

im Videozur Stelle im Video springen

(00:10)

Mit den Winkelfunktionen Sinus, Cosinus und Tangens kannst du Winkel und Seiten in einem rechtwinkligen Dreieck berechnen. Schau dir dazu ein rechtwinkliges Dreieck an:

Winkelfunktionen, winkelfunktion, winkelfunktionen formeln, winkelfunktionen dreieck, winkel funktion, winkelfunktion im dreieck, winkelfunktionen berechnen, rechtwinkliges Dreieck, Alpha, rechter Winkel, Katheten, Hypotenuse, Ankathete, Gegenkathete — Winkelfunktionen am rechtwinkligen Dreieck

Du siehst drei Seiten:

Hypotenuse: die längste Seite
Gegenkathete von α: Seite gegenüber vom Winkel α
Ankathete von α: Seite, die am Winkel α anliegt

Mit diesen Seiten kannst du für die Winkelfunktionen Formeln aufschreiben. Sie lauten:

$\sin(\alpha) = \frac{\text{\textcolor{red}{Gegenkathete}}}{\text{\textcolor{teal}{Hypotenuse}}}$

$\cos(\alpha) = \frac{\text{\textcolor{blue}{Ankathete}}}{\text{\textcolor{teal}{Hypotenuse}}}$

$\tan(\alpha) = \frac{\text{\textcolor{red}{Gegenkathete}}}{\text{\textcolor{blue}{Ankathete}}}$

Aber wie kannst du mit den Formeln der Winkelfunktionen rechnen? Schau dir das gleich genauer an!

Die Winkelfunktionen

Die Winkelfunktionen Sinus, Cosinus, Tangens und Cotangens (abgekürzt sin, cos, tan und cot) sind für einen gegebenen Winkel eine Zahl: Das Verhältnis zweier Seiten eines rechtwinkligen Dreiecks. Jede Winkelfunktion kann dir dabei helfen, fehlende Seiten oder Winkel in einem rechtwinkligen Dreieck zu bestimmen.

Winkelfunktion Sinus

Der Sinus von einem Winkel α ist das Verhältnis zwischen Gegenkathete und Hypotenuse, also

$\sin(\alpha) = \frac{\text{\textcolor{red}{Gegenkathete}}}{\text{\textcolor{teal}{Hyptenuse}}}$

Schau dir das gleich an einem Beispiel an:

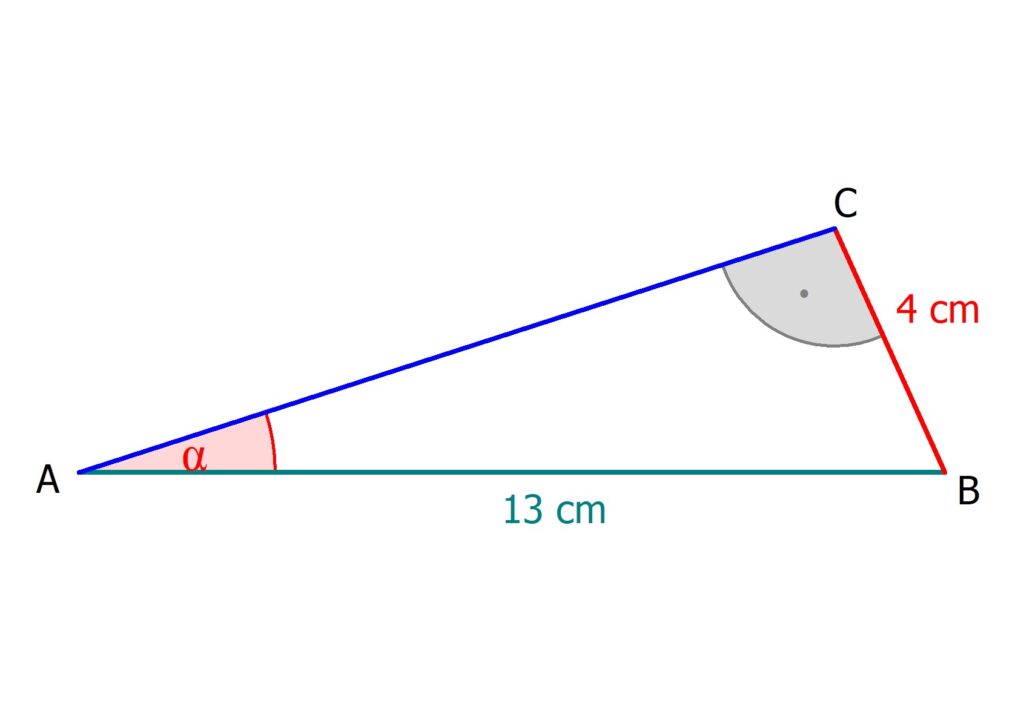
In einem Dreieck hat die Gegenkathete von α die Länge 4 cm und die Hypotenuse die Länge 13 cm. Wie groß ist dann der Winkel α?

Hier willst du einen Winkel mit Winkelfunktionen berechnen. Dabei gehst du immer so vor:

Schritt 1: Setze die Seitenlängen in die Winkelfunktion für den Sinus ein:
$\sin(\alpha) = \frac{\text{\textcolor{red}{Gegenkathete}}}{\text{\textcolor{teal}{Hyptenuse}}} = \frac{\textcolor{red}{4}}{\textcolor{teal}{13}}}$
Schritt 2: Du hast jetzt den Sinus von α, willst aber eigentlich α wissen! Deshalb brauchst du sin^-1. Das findest du als Taste auf deinem Taschenrechner. Gib einfach „sin^-1“ und dann das Ergebnis aus Schritt 1 ein:
$\sin(\alpha) = \frac{\textcolor{red}{4}}{\textcolor{teal}{13}}} \qquad \longrightarrow \qquad \alpha = \sin^{-1}(\frac{\textcolor{red}{4}}{\textcolor{teal}{13}}}) = 17,92^{\circ}$

Super! Der Winkel α ist also 17,92° groß!

Mehr über den Sinus erfährst du in unserem extra Beitrag dazu.

Winkelfunktion Cosinus

Die nächste Winkelfunktion ist der Cosinus. Der Cosinus von einem Winkel α ist das Verhältnis zwischen Ankathete und Hypotenuse, also

$\cos(\alpha) = \frac{\text{\textcolor{blue}{Ankathete}}}{\text{\textcolor{teal}{Hypotenuse}}}$

Schau dir auch hier gleich ein Beispiel an:

In einem Dreieck ist α = 60° und die Ankathete ist 6 cm lang. Wie lang ist die Hypotenuse?

Jetzt sollst du die Länge einer Seite mit Winkelfunktionen berechnen. Dann gehst du so vor:

Schritt 1: Schreibe die Formel für den Cosinus hin:
$\cos(\alpha) = \frac{\text{\textcolor{blue}{Ankathete}}}{\text{\textcolor{teal}{Hypotenuse}}}$
Schritt 2: Löse nach der gesuchten Seite auf. Hier ist das die Hypotenuse:
$\begin{align*} \cos(\alpha) &= \frac{\text{\textcolor{blue}{Ankathete}}}{\text{\textcolor{teal}{Hypotenuse}}} &&|\cdot \text{\textcolor{teal}{Hypotenuse}} \\ \cos(\alpha) \cdot \text{\textcolor{teal}{Hypotenuse}} &= \text{\textcolor{blue}{Ankathete}} &&|: \cos(\alpha) \\ \text{\textcolor{teal}{Hypotenuse}} &= \frac{\text{\textcolor{blue}{Ankathete}}}{\cos(\alpha)} \end{align*}$

Schritt 3: Setze die Zahlen ein:
$\text{\textcolor{teal}{Hypotenuse}} = \frac{\text{\textcolor{blue}{Ankathete}}}{\cos(\alpha)} = \frac{\text{\textcolor{blue}{6}}}{\cos(60^{\circ})} = 12$

Die Hypotenuse ist also 12 cm lang!

Wenn du mehr Aufgaben zum Cosinus sehen möchtest, dann schau dir unseren Beitrag dazu an!

Winkelfunktion Tangens

Schau dir als Nächstes die Formel zur Winkelfunktion Tangens an. Der Tangens von einem Winkel α ist das Verhältnis zwischen Gegenkathete und Ankathete, also

$\tan(\alpha) = \frac{\text{\textcolor{red}{Gegenkathete}}}{\text{\textcolor{blue}{Ankathete}}}$

Schau dir auch dazu ein Beispiel an:

In einem Dreieck ist α = 45° und die Ankathete 7 cm. Wie lang ist dann die Gegenkathete?

Du willst wieder die Länge einer Seite ausrechnen. Du gehst also so vor wie schon beim Cosinus:

Schritt 1: Schreibe die Formel für den Tangens hin:
$\tan(\alpha) = \frac{\text{\textcolor{red}{Gegenkathete}}}{\text{\textcolor{blue}{Ankathete}}}$
Schritt 2: Löse nach der gesuchten Seite auf. Hier ist das die Gegenkathete:
$\begin{align*} \tan(\alpha) &= \frac{\text{\textcolor{red}{Gegenkathete}}}{\text{\textcolor{blue}{Ankathete}}} &&|\cdot \text{\textcolor{blue}{Ankathete}} \\ \tan(\alpha) \cdot \text{\textcolor{blue}{Ankathete}} &= \text{\textcolor{red}{Gegenkathete}} \end{align*}$

Schritt 3: Setze die Zahlen ein:
$\text{\textcolor{red}{Gegenkathete}} = \tan(\alpha) \cdot \text{\textcolor{blue}{Ankathete}} = \tan(45^{\circ}) \cdot \textcolor{blue}{7} = 7$

Die Gegenkathete ist also 7 cm lang.

Weitere Beispiele zum Tangens findest du in unserem extra Beitrag dazu.

Übrigens: Wenn du den Zähler und den Nenner um die Hypotenuse erweiterst, bekommst du als Ergebnis

$\tan(\alpha) = \frac{\text{Gegenkathete}}{\text{Ankathete}} = \frac{\frac{\text{Gegenkathete}}{\text{Hypotenuse}}}{\frac{\text{Ankathete}}{\text{Hypotenuse}}} = \frac{\sin(\alpha)}{\cos(\alpha)}$

Du kannst dir also merken:

Sinus Cosinus Tangens

Der Tangens eines Winkels ist gerade der Quotient aus Sinus und Cosinus desselben Winkels.

Winkelfunktion Cotangens

Schau dir zum Schluss noch den Cotangens an. Der Cotangens ist der Kehrwert des Tangens und damit das Verhältnis zwischen Ankathete und Gegenkathete, also

$\cot(\alpha) = \frac{\text{\textcolor{blue}{Ankathete}}}{\text{\textcolor{red}{Gegenkathete}}}$

Schau dir gleich ein konkretes Beispiel an:

Im Dreieck ist α = 30° und die Gegenkathete hat die Länge 8 cm. Wie lang ist dann die Ankathete?

Du willst wieder die Länge einer Seite berechnen. Dann kannst du wie gewohnt vorgehen:

Schritt 1: Schreibe die Formel für den Tangens hin:
$\cot(\alpha) = \frac{\text{\textcolor{blue}{Ankathete}}}{\text{\textcolor{red}{Gegenkathete}}}$
Schritt 2: Löse nach der gesuchten Seite auf. Hier ist das die Ankathete:
$\begin{align*} \cot(\alpha) &= \frac{\text{\textcolor{blue}{Ankathete}}}{\text{\textcolor{red}{Gegenkathete}}} &&|\cdot \text{\textcolor{red}{Gegenkathete}} \\ \cot(\alpha) \cdot \text{\textcolor{red}{Gegenkathete}} &= \text{\textcolor{blue}{Ankathete}} \end{align*}$

Schritt 3: Setze die Zahlen ein:
$\text{\textcolor{blue}{Ankathete}} = \cot(\alpha) \cdot \text{\textcolor{red}{Gegenkathete}} = \cot(30^{\circ}) \cdot \textcolor{red}{8} = 8 \sqrt{3}$

Übrigens: Der Cotangens ist gerade der Kehrwert des Tangens. Das bedeutet:

$\cot(\alpha) = \frac{1}{\tan(\alpha)}$

Der Tangens ist der Quotient aus Sinus und Cosinus. Deshalb ergibt sich für den Cotangens auch die Beziehung

$\cot(\alpha) = \frac{1}{\tan(\alpha)} = \frac{\cos(\alpha)}{\sin(\alpha)}$

Hinweis: Auf den meisten Taschenrechnern gibt es keine eigene Taste für den Cotangens. Wenn du also die Formel zur Winkelfunktion für den Cotangens berechnen möchtest, musst du diese als den Kehrwert des Tangens bestimmen. Möchtest du mehr Gelegenheit zum Üben mit dem Cotangens erhalten, dann schaue dir auf jeden Fall unseren Beitrag dazu an.

Du kannst dir deshalb merken:

Sinus Cosinus Tangens und Cotangens

Der Cotangens eines Winkels ist gerade der Quotient aus Cosinus und Sinus oder der Kehrwert des Tangens.

Aufgaben: Winkelfunktionen Formeln

Schau dir noch zwei Aufgaben zu den Formeln der Winkelfunktionen an. In den Aufgaben werden Buchstaben für die Hypotenuse (c), die Gegenkathete von α (a) und die Ankathete von α (b) verwendet. Dann sind die Formeln für die Winkelfunktionen:

sin(α) = cos(β) = a/c
cos(α) = sin(β) = b/c
tan(α) = cot(β) = a/b

Bei den Aufgaben musst du selbst herausfinden, welche Winkelfunktion du verwenden musst. Dafür schaust du dir immer an, welche Seiten oder Winkel du gegeben hast (z. B. Gegenkathete von α und α) und welche du berechnen sollst (z. B. Hypotenuse). Dann suchst du die Formel, in der alle drei Werte vorkommen:

Im Beispiel: Gegenkathete von α, α und Hypotenuse → Sinus

Aufgabe 1: Winkelfunktionen berechnen

Du hast folgendes Dreieck gegeben:

Winkelfunktionen Aufgabe — Rechtwinkliges Dreieck für Aufgabe 1.

(a) Bestimme die fehlenden Winkel α und β.

(b) Berechne die fehlende Seite c unter Verwendung einer der Winkelfunktionen.

Lösung Aufgabe 1

(a) Berechne zuerst α. Weil du Gegenkathete und Ankathete gegeben hast, verwendest du den Tangens:

Schritt 1: Zahlen in die Formel einsetzen
$\tan(\alpha) = \frac{5}{7}$
Schritt 2: Nach dem Winkel auflösen
$\alpha = \tan^{-1}(\frac{5}{7}) = 35,54^{\circ}$

In einem Dreieck ist die Summe aller Winkel gleich 180°. Also gilt

$\alpha + \beta + 90^{\circ} = 180^{\circ}$

Das stellst du nach β um und bekommst

$\beta = 180^{\circ} - (\alpha + 90^{\circ}) = 54,46^{\circ}$

(b) Weil du die Ankathete von α kennst, kannst du den Cosinus verwenden:

Schritt 1: Formel aufstellen
$\cos(\alpha) = \frac{b}{c}$
Schritt 2: Formel umstellen
$c = \frac{b}{\cos(\alpha)}$
Schritt 3: Zahlen einsetzen
$c = \frac{b}{\cos(\alpha)} = 8,6$

Aufgabe 2: Winkelfunktionen berechnen

Das folgende Dreieck ist gegeben.

(a) Bestimme die fehlenden Seiten b und c.

(b) Berechne den fehlenden Winkel β.

Lösung Aufgabe 2

(a) Bestimme zuerst c. Du kennst α und die Gegenkathete von α und willst die Hypotenuse haben. Deshalb kannst du den Sinus verwenden:

Schritt 1: Formel aufstellen
$\sin(\alpha) = \frac{a}{c}$
Schritt 2: Formel umstellen
$c = \frac{a}{\sin(\alpha)}$
Schritt 3: Zahlen einsetzen
$c = \frac{a}{\sin(\alpha)} = 6$

Du willst nun noch b ausrechnen. Du kennst α und die Gegenkathete von α und möchtest die Ankathete von α ausrechnen. Verwende deshalb den Tangens:

Schritt 1: Formel aufstellen
$\tan(\alpha) = \frac{a}{b}$
Schritt 2: Formel umstellen
$b = \frac{a}{\tan(\alpha)}$
Schritt 3: Zahlen einsetzen
$b = \frac{a}{\tan(\alpha)} = 3 \sqrt{3}$

(b) In einem Dreieck ist die Summe aller Winkel gleich 180°. Deshalb gilt

$\alpha + \beta + 90^{\circ} = 180^{\circ}$

Stellst du das nach β um, bekommst du

$\beta = 180^{\circ} - (\alpha + 90^{\circ}) = 60^{\circ}$

Sinus Cosinus und Tangens für alle Winkel

im Videozur Stelle im Video springen

(02:16)

Die Definitionen der Formeln der Winkelfunktionen am rechtwinkligen Dreieck sind auf die Winkel von 0° bis 90° beschränkt. In diesem Abschnitt erweitern wir die Winkelfunktionen Sinus Cosinus und Tangens auf alle Winkel.

Sinus und Cosinus

Wir können die x- und y-Koordinate eines Punktes P auf dem Einheitskreis geometrisch folgendermaßen bestimmen: Wir zeichnen ein rechtwinkliges Dreieck, sodass der Punkt eine Ecke des Dreiecks und der Abstand zum Ursprung die Hypotenuse ist. Die Länge der Hypotenuse kennen wir. Sie beträgt genau 1, da alle Punkte auf dem Kreis per Definition den Abstand 1 zum Ursprung haben. Bilden wir das Verhältnis zwischen Gegenkathete und Hypotenuse, so erhalten wir

$\sin(\alpha) = \frac{y}{1} = y$

und für das Verhältnis Ankathete zu Hypotenuse

$\cos(\alpha) = \frac{x}{1} = x$

Das heißt, dass der Sinus gerade die y-Koordinate und der Cosinus die x-Koordinate des Punktes P ist. Zum Beispiel ist der Sinus des Winkels 180° gerade Null, da die y-Koordinate dieses Punktes Null ist. Der Cosinus zu diesem Winkel wäre -1, da die x-Koordinate dieses Punktes -1 ist.

Sinus am Einheitskreis, Cosinus am Einheitskreis — Winkelfunktionen Sinus und Cosinus am Einheitskreis.

Wenden wir auf diesen Punkt den Satz des Pythagoras an, so erhalten wir

$x^2 + y^2 = 1$

Nutzen wir jetzt die Beziehungen zwischen den Winkelfunktionen Sinus und Cosinus und den Koordinaten des Punktes, so ergibt sich

$x^2 + y^2 = (\cos(\alpha))^2 + (\sin(\alpha))^2 = 1$

Trigonometrischer Pythagoras

Für einen beliebigen Winkel α gilt

$\sin^2(\alpha) + \cos^2(\alpha) = 1$

Tangens

Für den Tangens müssen wir das Dreieck im Einheitskreis so lange skalieren, bis die Ankathete zum Winkel α gleich 1 ist (die Winkel im Dreieck bleiben unverändert). Der Punkt P mit den Koordinaten (x, y) wird dabei zum Punkt P‘ mit den Koordinaten (x‘, y‘). Bilden wir für dieses skalierte Dreieck das Verhältnis zwischen Gegenkathete und Ankathete, so erhalten wir

$\tan(\alpha) = \frac{\text{Gegenkathete}}{\text{Ankathete}} = \frac{y'}{1} = y'$

Das heißt, dass der Tangens gerade die y-Koordinate des Punktes P‘ ist. Beachte, wie die Gegenkathete beim skalierten Dreieck gerade tangential zum Einheitskreis ist. Daher kommt auch die Bezeichnung Tangens. Das folgende Bild illustriert die beschriebene Konstruktion, wobei das skalierte Dreieck nicht schraffiert dargestellt ist.

Tangens am Einheitskreis, Winkelfunktionen, Einheitskreis — Winkelfunktion Tangens am Einheitskreis.

Hinweis: Das Vorzeichen von tan(α) ist positiv, wenn die Koordinaten x‘ und y‘ des Punktes P‘ entweder beide positiv oder beide negativ sind. Ansonsten ist tan(α) negativ. Das heißt, im ersten und dritten Quadranten besitzt der Tangens positive Werte, im zweiten und vierten Quadranten hingegen negative Werte.

Winkelfunktionen Tabelle

Im Folgenden zeigen wir dir eine Tabelle für verschiedene Werte der Winkelfunktionen Sinus Cosinus und Tangens. Zusätzlich haben wir auch den Cotangens aufgenommen.

Winkel α	sin(α)	cos(α)	tan(α)	cot(α)
0°	0	1	0	n. d.
30°	$\frac{1}{2}$	$\frac{\sqrt{3}}{2}$	$\frac{\sqrt{3}}{3}$	$\sqrt{3}$
45°	$\frac{\sqrt{2}}{2}$	$\frac{\sqrt{2}}{2}$	1	1
60°	$\frac{\sqrt{3}}{2}$	$\frac{1}{2}$	$\sqrt{3}$	$\frac{\sqrt{3}}{3}$
90°	1	0	n. d.	0
180°	0	-1	0	n. d.
270°	-1	0	n. d.	0

Die Bezeichnung „n. d.“ ist die Abkürzung für „nicht definiert“, da sich für diese Winkel die Tangenskurve beziehungsweise die Cotangenskurve einer senkrechten Asymptote nähert.

Winkelfunktionen berechnen

Bei der Berechnung der Werte für die Winkelfunktionen musst du unbedingt darauf achten, ob die Winkel im Gradmaß oder im Bogenmaß angegeben sind. Im Fall der Tabelle von vorhin waren die Winkel alle im Gradmaß angegeben. Entsprechend musst du auch deinen Taschenrechner auf „DEG“ einstellen, wenn du die Werte nachrechnen möchtest.

Die Umrechnung zwischen Gradmaß und Bogenmaß basiert auf folgender Beziehung

$1 \pi = 180°$

Wenn du beispielsweise wissen möchtest, wie ein Winkel von x° in Bogenmaß lautet, dann rechnest du

$x =\frac{x^{\circ}}{180^{\circ}} \cdot \pi$

Auf deinem Taschenrechner findest du das Bogenmaß unter der Abkürzung „RAD“.

Wichtige Begriffe der Trigonometrie

Neben den hier genannten Winkelfunktionen Sinus , Cosinus und Tangens, sowie dem trigonometrischen Pythagoras, gibt es weitere wichtige Begriffe und Formeln in der Trigonometrie:

Zu jedem dieser Themen haben wir einen eigenen Beitrag für dich vorbereitet, schau ihn dir unbedingt an!

Du willst wissen, wie du die Winkelfunktionen in ein Koordinatensystem einzeichnen und sogar Nullstellen davon berechnen kannst? Dann ist unser Video zu trigonometrischen Funktionen genau das Richtige für dich! Schau es dir gleich an!

Funktionen

Funktionen - Grundlagen

Funktionen

Funktionen - fortgeschritten

Funktionen

Zuordnungen

Funktionen

Lineare Funktionen

Funktionen

Quadratische Funktionen

Funktionen

Trigonometrie

Funktionen

Trigonometrische Funktionen

Funktionen

Polynome

Funktionen

Polynomdivision

Funktionen

Rationale Funktionen

Funktionen

Exponentialfunktion

Funktionen

Logarithmus