Video

Quiz

Hier geht's zum Video „Kettenregel“

Hier geht's zum Video „e Funktion ableiten“

Hier geht's zum Video „e-Funktion integrieren“

Hier geht's zum Video „Jupiter“

Hier geht's zum Video „Asymptote“

Hier geht's zum Video „Grenzwert“

Hier geht's zum Video „Kurvendiskussion e-Funktion“

e Funktion einfach erklärt

Wichtige Inhalte in diesem Video

e Funktion einfach erklärt

Wie rechnest du mit der e Funktion?

E Funktionen ableiten

Stammfunktion ex / Integral

Schnittpunkte mit den Koordinatenachsen (Nullstellen e Funktion)

Du willst wissen, wie du mit der e Funktion rechnest und welche Eigenschaften sie hat? Alles von den Nullstellen der e Funktion bis zu ihrer Ableitung erklären wir dir hier und natürlich in unserem Video !

Inhaltsübersicht

e Funktion einfach erklärt

im Videozur Stelle im Video springen

Die e Funktion ist die natürliche Exponentialfunktion mit der Basis e ≈ 2,718. Ihre Gleichung ist:

f(x) = e^x

E Funktion, e-funktion, e funktionen, e hoch x, efunktion, e fkt, e funktion rechenregeln, e funktion regeln, e Funktionen addieren, e funktion eigenschaften, e regeln, e hoch 1, e hoch 0, e^x, e^-x, natürliche exponentialfunktion, e funktion nullstellen, e hoch minus x, e funktion reihe, exp funktion, e funktion graph, logarithmus e funktion, exponentialfunktion regeln, e funktion gesetze, exponentialfunktion rechenregeln, e rechenregeln, stammfunktion e^x, Graph, Schnittpunkt y-Achse, Punkte, Koordinatensystem, Funktion, Achsen — e Funktion Graph

Aufgepasst! Lass dich von dem e nicht verwirren. Das e ist eine ganz normale Zahl, so ähnlich wie π. Du nennst sie Eulersche Zahl .

Eigenschaften von e Funktionen

Keine Nullstellen: Die e-Funktion schneidet nie die x-Achse, nähert sich aber links immer mehr der x-Achse an.
Ableitung f'(x) = e^x: Die Ableitung von e hoch x ist gleich wie die e Funktion selbst.
Stammfunktion F(x) = e^x+ c: Auch die Stammfunktion e hoch x ist gleich wie die e-Funktion.
Umkehrfunktion f^-1(x) = ln(x): Die Umkehrfunktion ist der natürliche Logarithmus ln(x).
Rechenregeln: e⁰ = 1 und e¹ = e

Wie rechnest du mit der e Funktion?

im Videozur Stelle im Video springen

Oft musst du mit der e-Funktion rechnen, zum Beispiel wenn du Nullstellen oder Hoch- und Tiefpunkte herausfinden musst oder eine Gleichung lösen willst. Dafür solltest du dir zwei wichtige Gesetze der e Funktion und der ln Funktion merken:

E Funktion Regeln

ln(e^x) = x

e^ln(x) = x

Das e und der ln löschen sich also gegenseitig. Schau dir ein Beispiel dazu an:

$\begin{aligned} \textcolor{red}{e}^{4x} - 8 &= 0 \phantom{ln()} \qquad | + 8\\ \textcolor{red}{e}^{4x} &= 8 \phantom{ln()} \qquad | \ ln() \ auf \ beiden \ Seiten \\ \textcolor{blue}{ln}(\textcolor{red}{e}^{4x}) &= \textcolor{blue}{ln}(8) \qquad | \ \textcolor{red}{e} \ und \ \textcolor{blue}{ln} \ löschen \ sich \\ 4x &= \textcolor{blue}{ln}(8) \qquad | : 4\\ x &= \frac{\textcolor{blue}{ln}(8)}{4} \end{aligend}$

Wenn du e Funktionen addieren oder zusammenfassen willst, brauchst du manchmal auch e Funktion Rechenregeln:

E Funktion Rechenregeln

$e^{x+y} = e^x \cdot e^y$

$e^{x-y} = \cfrac{e^x}{e^y}$

$e^{x \cdot y} = \left( e^x\right)^y$

$e^{-x} = e^{-x} = \frac{1}{e^x}$

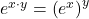
Schau dir auch ein Beispiel zu den e Rechenregeln an: Vereinfache (e^x)² • e^x

$(e^x)^2 \cdot e^x \overset{\text{Regel3}}{=} e^{2x} \cdot e^{x} \overset{\text{Regel1}}{=} e^{2x + x} = e^{3x}$

Zusätzlich zu den e Funktion Rechenregeln solltest du dir folgende Exponentialfunktion Regeln für e hoch 0 und e hoch 1 merken:

e hoch 0: e⁰ = 1
e hoch 1: e¹ = e
e hoch minus x: e^-x = 1/e^x

Achtung! Beim e Funktionen addieren musst du aufpassen. Wenn zwei e Funktionen unterschiedliche Hochzahlen haben, z.B. e^-x und e^2x, kannst du die e Funktionen nicht addieren: $\textcolor{red}{e^{-x}+e^{2x}\xcancel{=e^{-x+2x}}}$

E Funktionen ableiten

im Videozur Stelle im Video springen

Die Ableitung von e hoch x ist wieder e^x selbst:

Ableitung E Funktion

f(x) = e^x→ f'(x) = e^x

Wenn in der Hochzahl (Exponent) mehr als ein x steht, dann verwendest du zum Ableiten die Kettenregel :

$\begin{aligned} f(x) &= \textcolor{red}{e^{5x+4}} \\ \implies f'(x) &= \textcolor{red}{e^{5x+4}} \cdot textcolor{olive}{5} \end{aligned}$

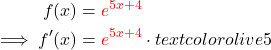
Den Teil e^Hochzahl lässt du stehen. Dahinter schreibst du „mal die Ableitung der Hochzahl.“

Wenn die e Funktionen komplizierter sind, zum Beispiel f(x) = x² • e^3x oder $f(x)=\frac{2x}{3e^x-1}$ , brauchst du die Produktregel oder die Quotientenregel :

$f(x) = \underbrace{\textcolor{blue}{x^2}}}_{u(x)} \cdot \underbrace{\textcolor{red}{e^{3x}}}_{v(x)}$

$\begin{aligned} \implies f'(x) &= u'(x) \cdot v(x) + u(x) \cdot v'(x) \\ &= \textcolor{blue}{2x} \cdot \textcolor{red}{e^{3x}} + \textcolor{blue}{x^2} \cdot \underbrace{\textcolor{red}{e^{3x} \cdot 3}}_{Kettenregel} \\ &= e^{3x} \cdot (2x + x^2 \cdot 3) \end{aligned}$

Im letzten Schritt hast du e^3x ausgeklammert. Das hilft dir später beim Weiterrechnen.

Dir ging alles etwas zu schnell? Dann schau dir doch unser ausführliches Video zur Ableitung der natürliche Exponentialfunktion an!

Stammfunktion e^x / Integral

im Videozur Stelle im Video springen

Die Stammfunktion bzw. das Integral der von e hoch x ist wieder die e-Funktion selbst:

Stammfunktion e^x

$F(x) = \int e^x dx = e^x+c$

Du möchtest noch eine ausführlichere Erklärung? Dann schau dir unser Video zum Integrieren von e^x an.

Eigenschaften der e Funktion

Bei einer Kurvendiskussion brauchst du einige Eigenschaften der e Funktion. Dazu zählen:

Schnittpunkte mit den Koordinatenachsen (Nullstellen e Funktion)
Grenzverhalten
Symmetrie
Definitionsmenge und Wertemenge
Monotonie
Umkehrfunktion

Die erklären wir dir jetzt genauer!

Schon gewusst? Die Eulersche Zahl

Die Eulersche Zahl e heißt so, weil sie von dem Mathematiker Leonhard Euler entdeckt wurde. Sie entsteht, wenn du unendlich oft bestimmte Brüche zusammenzählst (e Funktion Reihe):

$\sum\limits_{n=0}^\infty \cfrac{1}{n!} = \frac{1}{0!}+ \frac{1}{1!}+ \frac{1}{2!}+ \frac{1}{3!}+\ldots$

$=1+\frac{1}{1 }+\frac{1}{2\cdot 1}+\frac{1}{ 3 \cdot 2\cdot 1}+ \frac{1}{4 \cdot 3 \cdot 2\cdot 1} + \ldots= 2,7182\ldots = e$

Die Zahl e hat unendlich viele Nachkommastellen und du kannst sie nicht als Bruch darstellen.

Schnittpunkte mit den Koordinatenachsen (Nullstellen e Funktion)

im Videozur Stelle im Video springen

Der Schnittpunkt mit der y-Achse liegt bei der normalen e-Funktion f(x) = e^xbei (0|1). Die normale e-Funktion f(x) = e^x hat keinen Schnittpunkt mit der x-Achse. Sie hat also keine Nullstellen.

Bei anderen Funktionen (z.B. f(x) = 3e^2x-1) musst du die Schnittpunkte berechnen:

Schnittpunkt mit der y-Achse: Setze für x die 0 ein und rechne das aus.

$f(0) = 3\cdot e^{2 \cdot 0}-1=3 \cdot e^{0}-1 = 3 \cdot 1 - 1= 3 -1 = \textcolor{blue}{2}$ ⇒ Schnittpunkt bei (0|2)

Schnittpunkt mit der x-Achse (Nullstelle ): Setze die natürliche Exponentialfunktion gleich 0 und löse nach x auf.
$\begin{aligned}3e^{2x}-1 &= 0 \\x &= \frac{ln(\frac{1}{3})}{2}\end{aligned}$

Wie du diese Gleichung auflöst, erklären wir dir im Abschnitt „Wie rechnest du mit der e Funktion?“ weiter oben in diesem Beitrag. Die Nullstelle liegt also bei (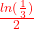 $\textcolor{red}{\frac{ln(\frac{1}{3})}{2}}$ | 0).

Grenzverhalten

im Videozur Stelle im Video springen

Beim Grenzverhalten schaust du dir an, was mit der Funktion für sehr große ( $+\infty$ ) oder sehr kleine ( $-\infty$ ) x-Werte passiert.

Verhalten im Unendlichen

Sehr große x-Werte (x → $+\infty$ ): $e^x \to +\infty$ , d.h. die y-Werte werden sehr groß
Sehr kleine x-Werte (x → $-\infty$ ): $e^x \to 0$ , d.h. die y-Werte gehen gegen 0

E Funktion, e-funktion, e funktionen, e hoch x, efunktion, e fkt, e funktion rechenregeln, e funktion regeln, e Funktionen addieren, e funktion eigenschaften, e regeln, e hoch 1, e hoch 0, e^x, e^-x, natürliche exponentialfunktion, e funktion nullstellen, e hoch minus x, e funktion reihe, exp funktion, e funktion graph, logarithmus e funktion, exponentialfunktion regeln, e funktion gesetze, exponentialfunktion rechenregeln, e rechenregeln, stammfunktion e^x, Graph, Koordinatensystem, Funktion, Achsen, x-Achse, y-Achse — Grenzwerte der exp Funktion

Die waagrechte Asymptote der exp Funktion ist also die x-Achse.

Wenn deine e-Funktion in einem Produkt steht (z.B. f(x) = — x² • e^x), gilt folgende Regel:

Wenn beide Faktoren gegen $\infty$ gehen, dann gelten die Vorzeichenregeln: $(-\infty)$ • $(+\infty)$ = $(-\infty)$ und $(-\infty)$ • $(-\infty)$ = $(+\infty)$ :

Beispiel: Für $x \to +\infty$ gilt: $\underbrace{-x^2}_{\to \textcolor{red}{-\infty}} \cdot \underbrace{e^x}_{\to \textcolor{olive}{+\infty}} \to \textcolor{red}{-\infty}$

Wenn ein Faktor des Produkts gegen 0 geht und der andere gegen $+\infty$ oder $-\infty$ , dann gewinnt immer die e-Funktion:

Beispiel: Für $x \to -\infty$ gilt: $\underbrace{-x^2}_{\to \textcolor{red}{-\infty}} \cdot \underbrace{e^x}_{\to \textcolor{blue}{0}} \to \textcolor{blue}{0}$

Symmetrie der e-Funktion

Die normale natürliche Exponentialfunktion f(x) = e^x ist nicht punktsymmetrisch und nicht achsensymmetrisch. Schau dir aber mal den e Funktion Graph von $f(x) = e^{x^2-1}$ an:

E Funktion, e-funktion, e funktionen, e hoch x, efunktion, e fkt, e funktion rechenregeln, e funktion regeln, e Funktionen addieren, e funktion eigenschaften, e regeln, e hoch 1, e hoch 0, e^x, e^-x, natürliche exponentialfunktion, e funktion nullstellen, e hoch minus x, e funktion reihe, exp funktion, e funktion graph, logarithmus e funktion, exponentialfunktion regeln, e funktion gesetze, exponentialfunktion rechenregeln, e rechenregeln, stammfunktion e^x , Graph, Koordinatensystem, Funktion, Achsen, x-Achse, y-Achse — Eine achsensymmetrische e Funktion

Du siehst, dass diese natürliche Exponentialfunktion achsensymmetrisch zur y-Achse ist. Um das mathematisch auszurechnen, musst du f(-x) berechnen und vereinfachen:

$\textcolor{orange}{f(-x)} = e^{(-x)^2-1} = e^{x^2-1} = f(x)$

Du siehst, dass (-x)² = x²ist, weil sich das Minus bei hoch 2 auflöst. Deshalb ist f(-x) das Gleiche ist wie f(x) selbst. Darum nennst du diese e Funktion achsensymmetrisch. Es gilt nämlich:

Symmetrie bei Funktionen

Achsensymmetrie : $\textcolor{orange}{f(-x)} = f(x)$

Punktsymmetrie : $\textcolor{orange}{f(-x)} = -f(x)$

Definitionsmenge und Wertemenge

Die Definitionsmenge sind die Zahlen, die du in eine Funktion einsetzen darfst. Alle Zahlen, die als y-Werte rauskommen können, nennst du Wertemenge .

Definitionsmenge und Wertemenge der exp Funktion

Du darfst alle Zahlen in e hoch x einsetzen, bekommst aber nur positive Zahlen heraus.

Definitionsmenge: $\mathbb{D}=\mathbb{R}$
Wertemenge: $\mathbb{W}=\mathbb{R}^+$

Monotonie

Die normale exp Funktion f(x) = e^x ist streng monoton wachsend. Das heißt, sie steigt die ganze Zeit an.

Bei anderen Funktionen bestimmst du das Monotonieverhalten mithilfe der Ableitung. Wie das geht, zeigen wir dir hier !

Umkehrfunktion

Die Umkehrfunktion der e-Funktion ist die ln-Funktion f^-1(x) = ln(x). Den ln nennst du auch natürlichen Logarithmus .

E Funktion, e-funktion, e funktionen, e hoch x, efunktion, e fkt, e funktion rechenregeln, e funktion regeln, e Funktionen addieren, e funktion eigenschaften, e regeln, e hoch 1, e hoch 0, e^x, e^-x, natürliche exponentialfunktion, e funktion nullstellen, e hoch minus x, e funktion reihe, exp funktion, e funktion graph, logarithmus e funktion, exponentialfunktion regeln, e funktion gesetze, exponentialfunktion rechenregeln, e rechenregeln, stammfunktion e^x, Graph, Koordinatensystem, Funktion, Achsen, x-Achse, y-Achse — e Funktion Graph und ln Funktion Graph

Den Logarithmus erhältst du aus der exp Funktion, wenn du e hoch x an der grünen Geraden spiegelst.

Wenn du dein Wissen zur E-Funktion noch zusätzlich vertiefen oder mehr Details erfahren willst, dann sieh dir gerne auch unseren fortgeschrittenen Beitrag dazu an!

Quiz zum Thema E Funktion einfach erklärt

ln Funktion

Willst du die Umkehrfunktion der e Funktion genauer kennenlernen? Dann schau dir direkt unser Video zur ln Funktion an. Bis gleich!

Zum Video: ln Funktion

zur Videoseite: E Funktion einfach erklärt

Beliebte Inhalte aus dem Bereich Funktionen

Exponentialfunktion

E Funktion einfach erklärt

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .