Video anzeigen

Sinussatz

Wichtige Inhalte in diesem Video

Der Sinussatz ist einer der wichtigsten Sätze der Trigonometrie. Hier und in unserem Video erfährst du, wie er geht, wie du damit rechnest und was er mit dem Kosinussatz zu tun hat!

Inhaltsübersicht

Sinussatz einfach erklärt

im Videozur Stelle im Video springen

(00:13)

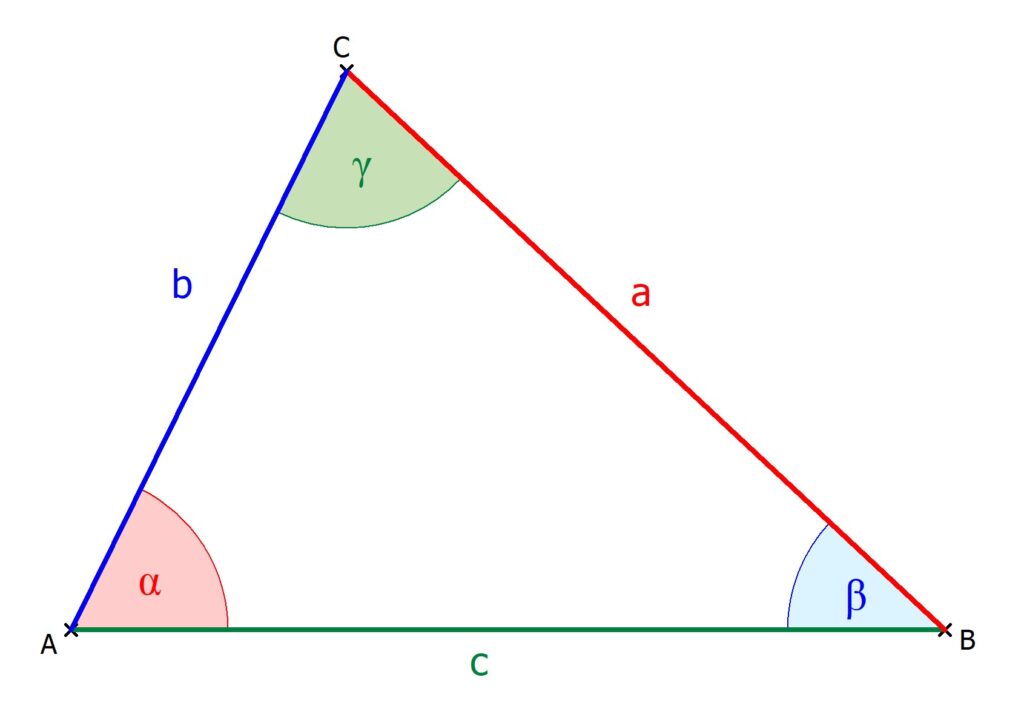
Mit dem Sinussatz kannst du Seiten und Winkel in jedem beliebigen Dreieck berechnen. Wenn du eine Seite und den gegenüberliegenden Winkel kennst, kannst du von einer anderen Größe (Seite oder Winkel) die gegenüberliegende Größe ausrechnen.

Du siehst am Dreieck, dass du die Seiten mit a, b und c und die Winkel mit α, β und γ bezeichnest. Damit kannst du den Sinussatz als Formel aufschreiben:

Sinussatz Formel

$\frac{\textcolor{red}{a}}{\sin(\textcolor{red}{\alpha})} = \frac{\textcolor{blue}{b}}{\sin(\textcolor{blue}{\beta})} = \frac{\textcolor{teal}{c}}{\sin(\textcolor{teal}{\gamma})}$

Aber wie kannst du damit konkret Seiten und Winkel ausrechnen? Das siehst du jetzt gleich an einem Beispiel.

Sinussatz Formel Beispiel

im Videozur Stelle im Video springen

(00:35)

Schau dir folgendes Dreieck an: b = 5, c = 3 und γ = 35°. Wie groß ist der Winkel β?

Du kennst die Seite c und den Winkel gegenüber, also γ. Deshalb kannst du den Sinussatz anwenden. Dann gehst du so vor:

Schritt 1: Suche dir aus dem Sinussatz die beiden Brüche, aus denen du Größen kennst. Hier sind das c, γ und b.

$\frac{\textcolor{blue}{b}}{\sin(\textcolor{blue}{\beta})} = \frac{\textcolor{teal}{c}}{\sin(\textcolor{teal}{\gamma})}$

Schritt 2: Sinussatz umstellen nach der gesuchten Größe.

$\begin{align*} \frac{\textcolor{blue}{b}}{\sin(\textcolor{blue}{\beta})} &= \frac{\textcolor{teal}{c}}{\sin(\textcolor{teal}{\gamma})} &|\cdot \sin(\beta) \\ \textcolor{blue}{b} &= \frac{\textcolor{teal}{c}}{\sin(\textcolor{teal}{\gamma})} \cdot \sin(\textcolor{blue}{\beta}) &|: \frac{c}{\sin(\gamma)} \\ \textcolor{blue}{b} \cdot \frac{\sin(\textcolor{teal}{\gamma})}{\textcolor{teal}{c}} &= \sin(\textcolor{blue}{\beta}) \end{align*}$

Schritt 3: Setze die Größen ein und berechne.

$\sin(\textcolor{blue}{\beta}) = \textcolor{blue}{b} \cdot \frac{\sin(\textcolor{teal}{\gamma})}{\textcolor{teal}{c}} = \textcolor{blue}{5} \cdot \frac{\sin(\textcolor{teal}{35^{\circ}})}{\textcolor{teal}{3}} \approx 0,956$

Jetzt hast du den Sinus von β ermittelt. Um auf β zu kommen, musst du noch sin^-1auf dein Ergebnis anwenden. sin^-1 findest du meistens als Taste auf deinem Taschenrechner:

$\sin(\textcolor{blue}{\beta}) = 0,956 \implies \textcolor{blue}{\beta} = \sin^{-1}(0,956) \approx 72,93^{\circ}$

Der Winkel β ist also ungefähr 73° groß.

Du willst noch mehr Aufgaben sehen? Weiter unten findest du viele Übungen mit Lösungen!

Sinussatz Kosinussatz

Auch mit dem Kosinussatz kannst du Seiten und Winkel in einem allgemeinen Dreieck berechnen. Der Satz hat drei verschiedene Varianten, je nachdem, welche Seiten und Winkel du suchst:

a² = b² + c² – 2bc • cos(α)

b² = a² + c² – 2ac • cos(β)

c² = a² + b² – 2ab • cos(γ)

Du kannst ihn also anwenden, wenn du

zwei Seiten und den eingeschlossenen Winkel kennst und die dritte Seite ausrechnen willst oder
drei Seiten kennst und die Winkel ausrechnen willst.

In diesen Fällen kannst du nicht die Sinussatz Formel anwenden!

Schon gewusst? Der Kosinussatz wird auch als verallgemeinerter Satz des Pythagoras bezeichnet. Der Satz des Pythagoras gilt nur in einem rechtwinkligen Dreieck. Dort ist also der Winkel γ immer 90°, also cos(γ) = cos(90°) = 0. Wenn du das in die dritte Variante vom Kosinussatz einsetzt, siehst du, dass dann c² = a² + b²herauskommt, also der Satz des Pythagoras.

Sinussatz Aufgaben

im Videozur Stelle im Video springen

(01:58)

Schau dir jetzt noch zwei Aufgaben zum Sinussatz an. Beide beinhalten das Umstellen des Sinussatzes und die Berechnung unbekannter Winkel und Seiten.

Aufgabe 1: Sinussatz umstellen

In einem allgemeinen Dreieck sind folgende Größen bekannt

$c = 6, \gamma = 25^{\circ}, \beta = 100^{\circ}$

(a) Bestimme den fehlenden Winkel $\alpha$ .

(b) Berechne die fehlenden Seiten und .

(c) Zeichne das Dreieck mit den korrekten Zahlenwerten (Zeichnung muss nicht maßstabsgetreu sein).

Lösung Aufgabe 1

(a) In einem Dreieck gilt für die Summe der Winkel

$\alpha + \beta + \gamma = 180$ °

Damit ergibt sich der fehlende Winkel

$\alpha = 180^{\circ} - (\beta + \gamma) = 180^{\circ} - (100^{\circ} + 25^{\circ}) = 55$ °.

(b) Nach dem Sinussatz gilt

$\frac{a}{\sin(\alpha)} = \frac{b}{\sin(\beta)} = \frac{c}{\sin(\gamma)}$

Demnach ergibt sich die Seite

$b = \sin(\beta) \cdot \frac{c}{\sin(\gamma)} = \sin(100^{\circ}) \cdot \frac{6}{\sin(25^{\circ})} = 14$

Auf ähnliche Weise gilt für die Seite a

$a = \sin(\alpha) \cdot \frac{c}{\sin(\gamma)} = \sin(55^{\circ}) \cdot \frac{6}{\sin(25^{\circ})} = 12$

(c) Das Dreieck mit den korrekten Zahlenwerten kann folgendermaßen aussehen. Beachte, dass die Form deines Dreiecks sich von dem hier gezeigten unterscheiden kann. Es kommt nicht auf die Form an, sondern auf die Angabe der Zahlenwerte an den richtigen Positionen.

Aufgabe 2: Sinussatz umstellen

In einem allgemeinen Dreieck sind folgende Größen bekannt

$a = 11, b = 15, \alpha = 45^{\circ}$

(a) Bestimme die fehlenden Winkel $\beta$ und $\gamma$ .

(b) Berechne die fehlende Seite

(c) Zeichne das Dreieck mit den korrekten Zahlenwerten (Zeichnung muss nicht maßstabsgetreu sein).

Lösung Aufgabe 2

(a) Nach der Sinussatz Formel gilt

$\frac{a}{\sin(\alpha)} = \frac{b}{\sin(\beta)} = \frac{c}{\sin(\gamma)}$

Demnach ergibt sich für den Winkel $\beta$

$\beta = \sin^{-1} \left(b \cdot \frac{\sin(\alpha)}{a} \right) = \sin^{-1} \left(15 \cdot \frac{\sin(45^{\circ})}{11} \right) = 75^{\circ}$

Für den Winkel $\gamma$ erhalten wir somit

$\gamma = 180^{\circ} - (\alpha + \beta) = 180^{\circ} - (45^{\circ} + 75^{\circ}) = 60$ °

(b) Nach dem Sinussatz gilt

$\frac{a}{\sin(\alpha)} = \frac{b}{\sin(\beta)} = \frac{c}{\sin(\gamma)}$

Die Seite ergibt sich somit zu

$c = \sin(\gamma) \cdot \frac{a}{\sin(\alpha)} = \sin(60^{\circ}) \cdot \frac{11}{\sin(45^{\circ})} = 13,5$

Sinussatz Herleitung

Du kannst jetzt den Sinussatz umstellen und Dreiecke damit berechnen. In diesem Abschnitt zeigen wir dir, wie du den Sinussatz herleiten kannst.

Hierzu betrachtest du folgendes Dreieck. Du hast eine zur Seite b senkrechte Linie eingezeichnet, die durch den Punkt B verläuft. Diese gestrichelt dargestellte Linie wird mit h_b bezeichnet und teilt das Dreieck in zwei rechtwinklige Teildreiecke $\Delta \text{ADB}$ und $\Delta \text{DCB}$ auf.

Herleitung Sinussatz, Sinussatz Herleitung, Spitzer Winkel Sinussatz — Sinussatz Herleitung.

Im Teildreieck $\Delta$ ADB gilt

$\sin(\alpha) = \frac{h_b}{c}$

und im Teildreieck $\Delta$ DCB

$\sin(\gamma) = \frac{h_b}{a}$ .

Entscheidend für die Herleitung ist die Beobachtung, dass sowohl für 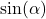$\sin(\alpha)$ als auch für $\sin(\gamma)$ die gestrichelte Linie h_b die Gegenkathete ist. Dividierst du nun die erste Gleichung durch die zweite Gleichung, erhältst du

$\frac{\sin(\alpha)}{\sin(\gamma)} = \frac{\frac{h_b}{c}}{\frac{h_b}{a}}$

und nach Kürzen des gemeinsamen Faktors h_b

$\frac{\sin(\alpha)}{\sin(\gamma)} = \frac{a}{c}$ .

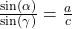Stellst du diese letzte Gleichung noch etwas um, so bekommst du

$\frac{a}{\sin(\alpha)} = \frac{c}{\sin(\gamma)}$ .

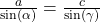Das ist gerade ein Teil des Sinussatzes. Auf ähnliche Weise kannst du die Höhen h_a (die zur Seite senkrechte Linie durch den Punkt ) und h_c (die zur Seite senkrechte Linie durch den Punkt ) einzeichnen. Auch diese beiden konstruierten Linien werden jeweils das Dreieck in zwei rechtwinklige Teildreiecke unterteilen. Analog zur vorhin gezeigten Berechnung erhalten wir die Gleichungen

$\frac{b}{\sin(\beta)} = \frac{c}{\sin(\gamma)}$ für die Höhe h_a und

$\frac{a}{\sin(\alpha)} = \frac{b}{\sin(\beta)}$ für die Höhe h_c

Insgesamt erhältst du also folgendes Resultat

$\frac{a}{\sin(\alpha)} = \frac{b}{\sin(\beta)} = \frac{c}{\sin(\gamma)}$

was gerade die Sinussatz Formel ist.

Hinweis: Wir haben hier den Sinussatz unter der Annahme hergeleitet, dass keiner der drei Winkel ein stumpfer Winkel ist. Der Sinussatz gilt aber auch, wenn ein Winkel größer als 90° ist. Die Herleitung dafür ist zwar ein wenig komplizierter, verläuft aber sehr ähnlich.

Sinus, Cosinus, Tangens

Du willst wissen, was du mit dem Sinus noch so alles machen kannst? Dann schau dir unser Video zu Sinus, Cosinus und Tangens an. Viel Spaß!

Beliebte Inhalte aus dem Bereich Funktionen

Eulersche Formel

Dauer: 04:27

Funktionen

Funktionen - Grundlagen

Funktionen

Funktionen - fortgeschritten

Funktionen

Zuordnungen

Funktionen

Lineare Funktionen

Funktionen

Quadratische Funktionen

Funktionen

Trigonometrie

Funktionen

Trigonometrische Funktionen

Funktionen

Polynome

Funktionen

Polynomdivision

Funktionen

Rationale Funktionen

Funktionen

Exponentialfunktion

Funktionen

Logarithmus

Funktionen

Fortgeschrittene trigonometrische Funktionen

Sinussatz

Sinussatz einfach erklärt

Sinussatz Formel Beispiel

Sinussatz Kosinussatz