Kosinussatz
Der Kosinussatz ist eine wichtige Formel in der Trigonometrie. Wie genau er lautet und wie du damit rechnest, erfährst du hier und in unserem Video !
Inhaltsübersicht
Kosinussatz einfach erklärt
Der Kosinussatz gibt dir die Beziehung zwischen den drei Seiten und einem Winkel in einem Dreieck an. Er hilft dir dabei,
- aus zwei Seiten und dem eingeschlossenen Winkel die dritte Seite zu berechnen
- aus drei Seiten einen Winkel zu berechnen.
Am Dreieck siehst du, dass du die Seiten mit a, b und c und die Winkel mit α, β und γ bezeichnest. Damit kannst du den Kosinussatz mathematisch aufschreiben. Er hat drei Varianten, je nach dem, welche Seiten und Winkel du suchst:
a2 = b2 + c2 – 2bc • cos(α)
b2 = a2 + c2 – 2ac • cos(β)
c2 = a2 + b2 – 2ab • cos(γ)
Aber wie wendest du den Satz an? Das erfährst du jetzt an einem Beispiel.
Kosinussatz Beispiel
Schau dir ein Dreieck mit den folgenden Seiten und Winkeln an: a = 3 cm, c = 5 cm und β = 75°. Wie lang ist die Seite b?
An der Skizze siehst du, dass du zwei Seiten und den eingeschlossenen Winkel β gegeben hast. Du kannst also den Kosinussatz anwenden. Dann gehst du so vor:
- Schritt 1: Suche die Variante des Kosinussatzes heraus, in der der gegebene Winkel vorkommt. Hier ist das die zweite Variante:
b2 = a2 + c2 – 2ac • cos(β)
- Schritt 2: Kosinussatz umstellen nach der gesuchten Größe. Hier suchst du b, also musst du nur die Wurzel ziehen.

- Schritt 3: Setze die Werte ein und rechne aus.
![Rendered by QuickLaTeX.com \[\textcolor{blue}{b} &= \sqrt{\textcolor{red}{a}^2 + \textcolor{teal}{c}^2 -2\textcolor{red}{a} \textcolor{teal}{c} \cdot \cos(\textcolor{blue}{\beta})} = \sqrt{\textcolor{red}{3}^2 + \textcolor{teal}{5}^2 -2\cdot \textcolor{red}{3} \cdot \textcolor{teal}{5} \cdot \cos(\textcolor{blue}{75^{\circ}})} = \sqrt{9 + 25 -30 \cdot \cos(\textcolor{blue}{75^{\circ}})} \approx 5,12 \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-efc7284a11410b02066dd0fb92e41aa3_l3.png)
Die Seite b ist also ungefähr 5,12 cm lang.
Schon gewusst? Der Kosinussatz wird manchmal auch als verallgemeinerter Satz des Pythagoras bezeichnet. Der Satz des Pythagoras gilt nämlich nur im rechtwinkligen Dreieck, also wenn γ = 90° ist. Dann ist cos(γ) = cos(90°) = 0. Wenn du das in die dritte Variante des Kosinussatzes einsetzt, erhältst du c2 = a2 + b2 , also genau den Satz des Pythagoras.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Kosinussatz Aufgaben
In diesem Abschnitt findest du noch zwei weitere Aufgaben zum Kosinussatz. Du musst beides mal den Kosinussatz umstellen und unbekannte Winkel und Seiten berechnen.
Achtung! Du kannst den Kosinussatz nur verwenden, wenn du zwei Seiten und den Winkel dazwischen kennst. Ist der Winkel gegenüber einer Seite bekannt, kann dir stattdessen oft der Sinussatz weiterhelfen.
Aufgabe 1: Kosinussatz umstellen
In einem allgemeinen Dreieck sind folgende Größen bekannt
 .
.
(a) Bestimme die fehlende Seite  .
.
(b) Berechne die fehlenden Winkel  und
und  .
.
(c) Zeichne das Dreieck mit den korrekten Zahlenwerten (Zeichnung muss nicht maßstabsgetreu sein).
Lösung Aufgabe 1
(a) Nach dem Kosinussatz gilt
 .
.
Einsetzen der gegebenen Zahlenwerte ergibt
 .
.
Durch Ziehen der Wurzel erhalten wir für die Seite 
 .
.
(b) Die Formel vom Kosinussatz sagt, dass

gilt. Umgestellt auf den Winkel  erhalten wir
erhalten wir
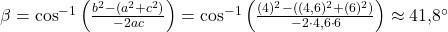 .
.
Der Winkel  ergibt sich dann zu
ergibt sich dann zu
 .
.
(c) Das Dreieck mit den korrekten Zahlenwerten kann folgendermaßen aussehen. Beachte, dass die Form deines Dreiecks sich von dem hier gezeigten unterscheiden kann. Es kommt nicht auf die Form an, sondern auf die Angabe der Zahlenwerten an den richtigen Positionen.
Aufgabe 2: Kosinussatz umstellen
In einem allgemeinen Dreieck sind folgende Größen bekannt
 .
.
(a) Bestimme die fehlende Seite  .
.
(b) Berechne die fehlenden Winkel  und
und  .
.
(c) Zeichne das Dreieck mit den korrekten Zahlenwerten (Zeichnung muss nicht maßstabsgetreu sein).
Lösung Aufgabe 2
(a) Nach dem Kosinussatz gilt
 .
.
Einsetzen der gegebenen Zahlenwerte ergibt
 .
.
Durch Ziehen der Wurzel erhalten wir für die Seite 
 .
.
(b) Die Formel vom Kosinussatz sagt, dass

gilt. Umgestellt auf den Winkel  erhalten wir
erhalten wir
 .
.
Der Winkel  ergibt sich dann zu
ergibt sich dann zu
 .
.
(c) Das Dreieck mit den korrekten Zahlenwerten kann folgendermaßen aussehen. Beachte, dass die Form deines Dreiecks sich von dem hier gezeigten unterscheiden kann. Es kommt nicht auf die Form an, sondern auf die Angabe der Zahlenwerten an den richtigen Positionen.
Kosinussatz Herleitung
Du kennst nun den Kosinussatz (Cosinussatz) und weißt, wie du ihn auf gesuchte Größen umstellen kannst. In diesem Abschnitt zeigen wir dir einen geometrischen Beweis für die Formel vom Kosinussatz.
Hierfür betrachten wir das folgende Dreieck. Wir haben eine zur Seite  senkrechte Linie eingezeichnet, die durch den Punkt
senkrechte Linie eingezeichnet, die durch den Punkt  verläuft. Diese gestrichelt dargestellte Linie wird mit
verläuft. Diese gestrichelt dargestellte Linie wird mit  bezeichnet und teilt das Dreieck in zwei rechtwinklige Teildreiecke
bezeichnet und teilt das Dreieck in zwei rechtwinklige Teildreiecke  ADB und
ADB und  DCB auf. Zusätzlich wird die Seite
DCB auf. Zusätzlich wird die Seite  in den zwei Teilseiten
in den zwei Teilseiten  und
und  (orange dargestellt) zerlegt. Ziel ist es, einen Zusammenhang zwischen den Seiten
(orange dargestellt) zerlegt. Ziel ist es, einen Zusammenhang zwischen den Seiten  und
und  , den dazwischen liegenden Winkel
, den dazwischen liegenden Winkel  und der gegenüberliegenden Seite
und der gegenüberliegenden Seite  zu finden.
zu finden.
Im Teildreieck  ADB gilt nach dem Satz des Pythagoras
ADB gilt nach dem Satz des Pythagoras
 .
.
Wir müssen nun versuchen, die Länge  und die Länge
und die Länge  durch die Seiten
durch die Seiten  und
und  sowie den Winkel
sowie den Winkel  zu ersetzen. Zunächst halten wir fest, dass im Teildreieck
zu ersetzen. Zunächst halten wir fest, dass im Teildreieck  DCB gilt
DCB gilt
 .
.
Ebenso gilt in diesem Teildreieck

oder umgestellt nach 
 .
.
Weiterhin gilt

oder umgestellt nach 
 .
.
Setzen wir diese Informationen in die erste Gleichung für  ein, so erhalten wir
ein, so erhalten wir

und unter Anwendung der Binomischen Formel
 .
.
Die Zahl  hebt sich auf und unser Endresultat lautet
hebt sich auf und unser Endresultat lautet
 ,
,
was gerade die Aussage vom Kosinussatz ist.
Auf ähnliche Weise kannst du die Höhen  (die zur Seite
(die zur Seite  senkrechte Linie durch den Punkt
senkrechte Linie durch den Punkt  ) und
) und  (die zur Seite
(die zur Seite  senkrechte Linie durch den Punkt
senkrechte Linie durch den Punkt  ) einzeichnen. Auch diese beiden konstruierten Linien werden jeweils das Dreieck in zwei rechtwinklige Teildreiecke unterteilen. Analog zur vorhin gezeigten Berechnung erhalten wir die Gleichungen
) einzeichnen. Auch diese beiden konstruierten Linien werden jeweils das Dreieck in zwei rechtwinklige Teildreiecke unterteilen. Analog zur vorhin gezeigten Berechnung erhalten wir die Gleichungen
 für die Höhe
für die Höhe  und
und
 für die Höhe
für die Höhe  .
.
Hinweis: Wir haben hier die Kosinussatz Formel unter der Annahme hergeleitet, dass keiner der drei Winkel ein stumpfer Winkel ist. Der Kosinussatz gilt aber auch, wenn ein Winkel größer als 90° ist. Die Herleitung dafür ist zwar ein wenig komplizierter, verläuft aber sehr ähnlich.
Cosinus, Sinus und Tangens
Super du kannst jetzt den Kosinussatz anwenden um fehlende Seiten und Winkel in einem allgemeinen Dreieck zu berechnen! In einem Dreieck mit rechtem Winkel verwendest du dafür den Sinus , Cosinus oder Tangens. Der Tangens zeigt im rechtwinkligen Dreieck das Verhältnis zwischen Gegenkathete und Ankathete.
![Rendered by QuickLaTeX.com \[tan(x) = \frac{Gegenkathete}{Ankathete} = \frac{sin(x)}{cos(x)}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-c08d2b3a2705d55e3f1a30a953cfb534_l3.png)
Um fehlende Werte im Dreieck in jeder Situation berechnen zu können, solltest du dir jetzt unbedingt noch unser Video dazu anschauen!





