Sinus
In diesem Beitrag beschäftigen wir uns mit dem Sinus. Unter anderem erfährst du, wie er am rechtwinkligen Dreieck und am Einheitskreis definiert ist.
Du möchtest den Sinus in kurzer Zeit erlernen? Dann schaue dir einfach unser Video zu diesem Thema an.
Inhaltsübersicht
Sinus einfach erklärt
Der Sinus ist eine wichtige trigonometrische Funktion, mit welcher du zum einen Winkel in einem rechtwinkligen Dreieck berechnen kannst und zum anderen ist er sehr nützlich, um periodische Vorgänge in der Physik zu beschreiben, wie zum Beispiel Wellen. Dabei beschreibt der Sinus das Verhältnis der Gegenkathete zur Hypotenuse eines Dreiecks. Mit bestimmten Überlegungen an einem Einheitskreis, kannst du mit Hilfe dieses Verhältnisses eine periodische Funktion konstruieren, die Sinusfunktion.
Sinus am rechtwinkligen Dreieck
Unsere Situation beginnt mit einem rechtwinkligen Dreieck. In diesem Dreieck soll einer der beiden Winkel, der nicht 90° ist, mit  bezeichnet werden. Die Seite, die diesem Winkel gegenüberliegt, heißt Gegenkathete. Die Seite, die dem rechten Winkel gegenüberliegt, heißt Hypotenuse und die letzte Seite wird als Ankathete bezeichnet.
bezeichnet werden. Die Seite, die diesem Winkel gegenüberliegt, heißt Gegenkathete. Die Seite, die dem rechten Winkel gegenüberliegt, heißt Hypotenuse und die letzte Seite wird als Ankathete bezeichnet.
Für ein solches Dreieck wird das Verhältnis von Gegenkathete zu Hypotenuse, also

als Sinus bezeichnet.
Bezeichnen wir die Gegenkathete mit  und die Hypotenuse mit
und die Hypotenuse mit  , dann ist der Sinus des Winkels
, dann ist der Sinus des Winkels  definiert als
definiert als
 .
.
Hinweis: Vielleicht fragst du dich, wie das in einem Dreieck aussieht, wo kein rechter Winkel vorhanden ist. In einem solchen Fall kann der sogenannte Sinussatz weiterhelfen. In unserem extra Beitrag erfährst du mehr darüber.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Definition am Einheitskreis
Wir können die  -Koordinate eines Punktes
-Koordinate eines Punktes  auf dem Einheitskreis geometrisch folgendermaßen bestimmen: Wir zeichnen ein rechtwinkliges Dreieck, sodass der Punkt eine Ecke des Dreiecks und der Abstand zum Ursprung die Hypotenuse wird. Die Länge der Hypotenuse kennen wir. Sie beträgt genau 1, da alle Punkte auf dem Kreis per Definition den Abstand 1 zum Ursprung haben. Bilden wir das Verhältnis zwischen Gegenkathete und Hypotenuse, so erhalten wir
auf dem Einheitskreis geometrisch folgendermaßen bestimmen: Wir zeichnen ein rechtwinkliges Dreieck, sodass der Punkt eine Ecke des Dreiecks und der Abstand zum Ursprung die Hypotenuse wird. Die Länge der Hypotenuse kennen wir. Sie beträgt genau 1, da alle Punkte auf dem Kreis per Definition den Abstand 1 zum Ursprung haben. Bilden wir das Verhältnis zwischen Gegenkathete und Hypotenuse, so erhalten wir
 .
.
Das heißt, dass der Sinus gerade die  -Koordinate des Punktes ist. Und dies gilt für alle Werte von
-Koordinate des Punktes ist. Und dies gilt für alle Werte von  . Zum Beispiel ist der Sinus des Winkels 180° gerade Null, da die
. Zum Beispiel ist der Sinus des Winkels 180° gerade Null, da die  -Koordinate dieses Punktes Null ist.
-Koordinate dieses Punktes Null ist.
Darstellung in einem Koordinatensystem
Um zu sehen, wie sich der Wert des Sinus als Funktion des Winkels  verhält, lassen wir den Winkel
verhält, lassen wir den Winkel  einmal um den Einheitskreis laufen und notieren uns für jeden
einmal um den Einheitskreis laufen und notieren uns für jeden  -Wert die
-Wert die  -Koordinate des Punktes.
-Koordinate des Punktes.
Die  -Koordinaten wiederholen sich nach einer ganzen Umdrehung. Wir können also erwarten, dass die Kurve des Sinus im Koordinatensystem das widerspiegeln wird. Weiterhin kann die
-Koordinaten wiederholen sich nach einer ganzen Umdrehung. Wir können also erwarten, dass die Kurve des Sinus im Koordinatensystem das widerspiegeln wird. Weiterhin kann die  -Koordinate nie größer als 1 beziehungsweise kleiner als -1 werden, da der Punkt auf dem Einheitskreis „gefangen“ ist. Entsprechend erwarten wir, dass auch die Kurve des Sinus keine größeren Werte als 1 annimmt (beziehungsweise keine kleineren Werte als -1 für die Punkte unterhalb der
-Koordinate nie größer als 1 beziehungsweise kleiner als -1 werden, da der Punkt auf dem Einheitskreis „gefangen“ ist. Entsprechend erwarten wir, dass auch die Kurve des Sinus keine größeren Werte als 1 annimmt (beziehungsweise keine kleineren Werte als -1 für die Punkte unterhalb der  -Achse). Das folgende Bild soll die geometrische Konstruktion der Kurve zeigen.
-Achse). Das folgende Bild soll die geometrische Konstruktion der Kurve zeigen.
Die Kurve, die den Verlauf der  -Koordinate in Abhängigkeit des Winkels
-Koordinate in Abhängigkeit des Winkels  zeigt, heißt Sinuskurve. Die Sinuskurve ist das Bild der sogenannten Sinusfunktion
. In unserem extra Beitrag erfährst du mehr über ihre Eigenschaften.
zeigt, heißt Sinuskurve. Die Sinuskurve ist das Bild der sogenannten Sinusfunktion
. In unserem extra Beitrag erfährst du mehr über ihre Eigenschaften.
Eine wichtige Eigenschaft, die dir vielleicht sofort aufgefallen ist, ist die Periodizität des Sinus. Das heißt, dass sich ein bestimmtes Muster (was der Bewegung einmal um den Kreis entspricht) ständig wiederholt. Genau diese Charakteristik macht die Sinusfunktion zu einem sehr nützlichen Werkzeug, um beispielsweise Wellenphänomene in der Physik oder Schaltkreise in der Elektrotechnik zu beschreiben.
Sinus berechnen
Einige Werte für den Sinus kannst du direkt anhand der Definition am Einheitskreis bestimmen. So ist zum Beispiel der Sinus von 90° genau 1, da die  -Koordinate des Punktes für diesen Winkel gerade 1 ist. Die folgende Tabelle zeigt die wichtigsten Werte.
-Koordinate des Punktes für diesen Winkel gerade 1 ist. Die folgende Tabelle zeigt die wichtigsten Werte.
 |
0° | 30° | 45° | 60° | 90° | 120° | 150° | 180° |
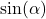 |
0 |  |
 |
 |
1 |  |
 |
0 |
 |
210° | 240° | 270° | 300° | 330° | 360° |
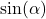 |
 |
 |
-1 |  |
 |
0 |
Eine andere Möglichkeit Winkel anzugeben, ist das Bogenmaß. Die Umrechnung basiert auf folgender Beziehung
 °.
°.
Wenn du beispielsweise wissen möchtest, wie ein Winkel von  ° im Bogenmaß lautet, dann rechnest du
° im Bogenmaß lautet, dann rechnest du
 .
.
Auf deinem Taschenrechner findest du das Winkelmaß unter der Abkürzung „rad“ für englisch „radian“.
Die Sinus Tabelle von vorhin sieht dann im Bogenmaß folgendermaßen aus.
 |
0 | 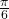 |
 |
 |
 |
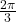 |
 |
 |
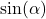 |
0 |  |
 |
 |
1 |  |
 |
0 |
 |
 |
 |
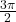 |
 |
 |
 |
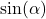 |
 |
 |
-1 |  |
 |
0 |
Wichtige Begriffe der Trigonometrie
Neben dem Sinus gibt es noch weitere Funktionen und wichtige Begriffe in der Trigonometrie, welche du kennen solltest.
- Winkelfunktionen
- Einheitskreis
- Cosinus
- Tangens
-
Cotangens
- Arcustangens (arctan)
- Additionstheoreme
- Sinussatz
- Kosinussatz .
In den extra Beiträgen erfährst du mehr dazu!
Sinus Aufgaben
In diesem Abschnitt rechnen wir gemeinsam zwei Aufgaben zum Sinus aus.
Lösung Aufgabe 1
(a) Nach dem Satz des Pythagoras gilt
 .
.
Setzen wir in diese Gleichung die gegebenen Werte für die Seiten  und
und  ein, so erhalten wir
ein, so erhalten wir

und nach ziehen der Wurzel
 .
.
(b) Es gilt
 .
.
Wenden wir auf beiden Seiten die Umkehrfunktion an, so erhalten wir
 °.
°.
In einem Dreieck ist die Summe aller Winkel gleich 180°. Demnach ergibt sich der fehlende Winkel  zu
zu
 .
.
Sinus — häufigste Fragen
(ausklappen)
Sinus — häufigste Fragen
(ausklappen)-
Was bedeutet der Sinus im rechtwinkligen Dreieck?Der Sinus im rechtwinkligen Dreieck bedeutet das Verhältnis der Gegenkathete zur Hypotenuse bezogen auf einen spitzen Winkel
 . Deshalb gilt
. Deshalb gilt  . Konkret: Liegt eine Seite dem Winkel
. Konkret: Liegt eine Seite dem Winkel  gegenüber, geht genau diese Länge in den Zähler.
gegenüber, geht genau diese Länge in den Zähler.
-
Wie erkenne ich im Dreieck die Gegenkathete zum Winkel α?Du erkennst die Gegenkathete zum Winkel
 daran, dass sie dem Winkel
daran, dass sie dem Winkel  direkt gegenüberliegt, also die Seite ist, die den Winkel
direkt gegenüberliegt, also die Seite ist, die den Winkel  nicht berührt. Beispiel: Markiere
nicht berührt. Beispiel: Markiere  an einer Ecke und nimm dann die Seite auf der gegenüberliegenden Dreiecksseite als Gegenkathete.
an einer Ecke und nimm dann die Seite auf der gegenüberliegenden Dreiecksseite als Gegenkathete.
-
Warum funktioniert die Sinus-Definition im Dreieck nur bis 90 Grad?Die Sinus-Definition
 im rechtwinkligen Dreieck funktioniert nur für Winkel kleiner als 90°, weil in einem rechtwinkligen Dreieck die beiden nicht-rechten Winkel spitz sind. Für größere Winkel erweitert man die Definition über den Einheitskreis auf alle
im rechtwinkligen Dreieck funktioniert nur für Winkel kleiner als 90°, weil in einem rechtwinkligen Dreieck die beiden nicht-rechten Winkel spitz sind. Für größere Winkel erweitert man die Definition über den Einheitskreis auf alle  .
.
-
Was bedeutet der Sinus am Einheitskreis als y-Koordinate?Der Sinus am Einheitskreis bedeutet:
 ist die
ist die  -Koordinate des Punktes auf dem Einheitskreis, der zum Winkel
-Koordinate des Punktes auf dem Einheitskreis, der zum Winkel  gehört. Das liegt daran, dass die Hypotenuse dort immer die Länge 1 hat und damit
gehört. Das liegt daran, dass die Hypotenuse dort immer die Länge 1 hat und damit  .
.
-
Warum kann der Sinus nur Werte zwischen minus 1 und 1 haben?Der Sinus kann nur Werte zwischen -1 und 1 haben, weil
 am Einheitskreis die
am Einheitskreis die  -Koordinate eines Punktes ist. Da alle Punkte auf dem Einheitskreis den Abstand 1 zum Ursprung haben, kann die
-Koordinate eines Punktes ist. Da alle Punkte auf dem Einheitskreis den Abstand 1 zum Ursprung haben, kann die  -Koordinate nie größer als 1 oder kleiner als -1 werden.
-Koordinate nie größer als 1 oder kleiner als -1 werden.
Lösung Aufgabe 2
(a) In einem Dreieck ist die Summe aller Winkel gleich 180°. Demnach berechnet sich der fehlende Winkel  zu
zu
 .
.
(b) Es gilt
 .
.
Stellen wir diese Gleichung nach  um, so erhalten wir
um, so erhalten wir
 .
.
Nach dem Satz des Pythagoras gilt
 .
.
Umgestellt auf  erhalten wir
erhalten wir

und nach Einsetzen der Werte für  und
und 
 .
.
Durch Wurzelziehen erhalten wir schließlich
 .
.




