Steigungsdreieck
Du möchtest verstehen, was ein Steigungsdreieck ist und wie du es am besten berechnest und zeichnest? Dann bist du hier genau richtig, denn wir erklären es dir mit vielen Bildern und Beispielen!
Du verstehst es besser, wenn es dir jemand anschaulich erklärt? Dann schau dir unbedingt unser Video dazu an.
Inhaltsübersicht
Steigungsdreieck einfach erklärt
Ein Steigungsdreieck brauchst du immer dann, wenn du von einer Funktion die Steigung berechnen willst.
Es gibt dir an, wie stark sich eine Funktion in einem bestimmten Intervall verändert, also wie groß ihre Steigung ist. Steigungsdreiecke können dabei unterschiedlich groß und an verschiedenen Stellen eingezeichnet werden. Bei linearen Funktionen macht das keinen Unterschied. Am häufigsten wirst du das Steigungsdreieck verwenden, um die Funktionsgleichung einer linearen Funktion zu bestimmen, konkret bedeutet das, die Steigung m einer Geraden f(x) = m • x + t herauszufinden.
Prinzipiell kannst du damit aber für jede Funktion mit zwei gegebenen Punkten die durchschnittliche Steigung bestimmen.
Steigungsdreieck zeichnen
Angenommen, du hast den Funktionsgraphen einer linearen Funktion gegeben und willst nun an der Geraden ein Steigungsdreieck einzeichnen, dann gehst du dabei wie folgt vor:
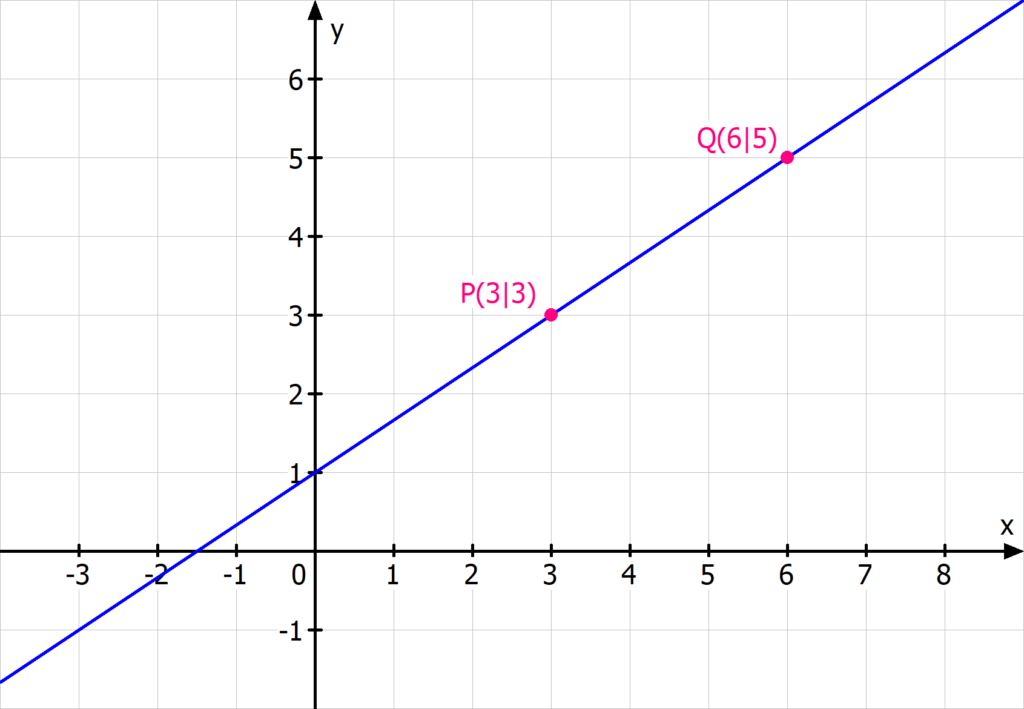
- Schritt 1: Wähle zwei beliebige Punkte auf der Geraden aus. Besonders geschickt ist es, die Punkte so zu wählen, dass sie direkt auf einem Kästchen liegen. Hier im Bild wählen wir deshalb P(3|3) und Q(6|5).
- Schritt 2: Bestimme den Punkt C, indem du von P ausgehend waagrecht nach rechts läufst und von Q senkrecht nach unten. Der Schnittpunkt der beiden gestrichelten Linien ist der Punkt C.
- Schritt 3: Zeichne nun das rechtwinklige Steigungsdreieck PQC ein.
Achtung: Da die beiden Punkte P und Q frei wählbar sind, kannst du ganz verschiedene Steigungsdreiecke einzeichnen. Klassischerweise zeichnet man es aber bei steigenden Funktionen unterhalb der Funktion ein und bei fallenden Geraden oberhalb.
Mit einem Steigungsdreieck kannst du die Steigung m einer Geraden bestimmen. Es gibt an, wie stark eine Funktion steigt bzw. fällt. Besonders nützlich ist das Steigungsdreieck, wenn du die Funktionsgleichung f(x) = mx + t einer linearen Funktion angeben willst.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Steigungsdreieck Formel
Wie genau du mit einem Steigungsdreieck eine Steigung  einer Geraden ausrechnest, zeigen wir dir jetzt.
einer Geraden ausrechnest, zeigen wir dir jetzt.
Mit den Punkten  und
und  ergibt sich die Steigung
ergibt sich die Steigung

Angenommen du hast einen Funktionsgraphen einer linearen Funktion (also eine Gerade) gegeben, und möchtest ihre Steigung bestimmen. Dann führst du die folgenden Schritte aus:
-
Schritt 1: Zeichne wie oben beschrieben ein Steigungsdreieck ein. Wähle dazu zuerst zwei beliebige Punkte
 und
und  .
.
-
Schritt 2: Bestimme als nächstes den Abstand der x-Werte
 und den Höhenunterschied
und den Höhenunterschied  . Du kannst dabei entweder die Kästchen zählen, oder du berechnest den Wert aus den Koordinaten der beiden Punkte
. Du kannst dabei entweder die Kästchen zählen, oder du berechnest den Wert aus den Koordinaten der beiden Punkte  und
und  . Dazu ziehst du jeweils die beiden x-Werte und die beiden y-Werte voneinander ab:
. Dazu ziehst du jeweils die beiden x-Werte und die beiden y-Werte voneinander ab:
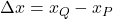

-
Schritt 3: Berechne nun die Steigung
 als
als

Beispiel 2: Steigungsdreieck berechnen
Hier wollen wir die Steigung der oben abgebildeten Geraden explizit berechnen. Hier sind  und
und  gegeben. Um
gegeben. Um  zu bestimmen, berechnen wir zuerst
zu bestimmen, berechnen wir zuerst


Die beiden Ergebnisse setzen wir jetzt in die Formel ein und erhalten für die Steigung der Geraden

Steigungsdreieck — häufigste Fragen
(ausklappen)
Steigungsdreieck — häufigste Fragen
(ausklappen)-
Was zeigt mir ein Steigungsdreieck bei einer Geraden?Ein Steigungsdreieck bei einer Geraden zeigt dir, wie stark die Gerade steigt oder fällt, wenn du in x-Richtung nach rechts gehst. Es macht den Zusammenhang zwischen der waagrechten Änderung
 und der senkrechten Änderung
und der senkrechten Änderung  sichtbar und hilft so, die Steigung zu bestimmen.
sichtbar und hilft so, die Steigung zu bestimmen.
-
Warum ist die Steigung gleich, egal wo ich das Steigungsdreieck einzeichne?Bei einer Geraden ist die Steigung überall gleich, weil sich
 und
und  entlang der Geraden immer im gleichen Verhältnis ändern. Deshalb können Steigungsdreiecke unterschiedlich groß sein oder an verschiedenen Stellen liegen, ohne dass sich die Steigung ändert.
entlang der Geraden immer im gleichen Verhältnis ändern. Deshalb können Steigungsdreiecke unterschiedlich groß sein oder an verschiedenen Stellen liegen, ohne dass sich die Steigung ändert.
-
Wie wähle ich zwei Punkte auf der Geraden, damit ich gut rechnen kann?Zwei Punkte wählst du so, dass sie genau auf Gitterpunkten liegen, also direkt auf Kästchen-Ecken. Dann lassen sich
 und
und  leicht ablesen oder aus den Koordinaten berechnen. Zum Beispiel sind P(3|3) und Q(6|5) dafür besonders geschickt.
leicht ablesen oder aus den Koordinaten berechnen. Zum Beispiel sind P(3|3) und Q(6|5) dafür besonders geschickt.
-
Wie finde ich den dritten Punkt beim rechtwinkligen Steigungsdreieck?Den dritten Punkt C findest du, indem du von einem Punkt waagrecht und vom anderen Punkt senkrecht gehst, bis sich beide Linien schneiden. Zum Beispiel gehst du von P waagrecht nach rechts und von Q senkrecht nach unten; der Schnittpunkt ist C und damit entsteht das rechtwinklige Dreieck PQC.
-
Wie berechne ich die Steigung aus Delta y und Delta x?Die Steigung berechnest du mit
 , also Höhenunterschied durch waagrechten Abstand. Dabei gilt
, also Höhenunterschied durch waagrechten Abstand. Dabei gilt  und
und  . Beispiel: Für P(-3|2) und Q(5|6) ist
. Beispiel: Für P(-3|2) und Q(5|6) ist  ,
,  und damit
und damit  .
.
Steigung berechnen
Steigungen kannst du nicht nur mit einem Dreieck bestimmen. Noch schneller geht das, wenn du sie einfach direkt berechnest! Wie das funktioniert, erfährst du in unserem Video .