Video

Quiz

Hier geht's zum Video „Steigung berechnen“

Hier geht's zum Video „Steigungsdreieck“

Hier geht's zum Video „Umkehrfunktion“

Steigungswinkel

Wichtige Inhalte in diesem Video

Steigungswinkel berechnen einfach erklärt

Steigungswinkel berechnen – Gerade

Schnittwinkel mit den Koordinatenachsen

In diesem Artikel erklären wir dir, was es mit dem Steigungswinkel einer linearen Funktion auf sich hat und wie du ihn am besten berechnest.

Wenn dir Videos lieber sind als lange Texte zu lesen, dann schau dir unser kurzes Video zum Steigungswinkel berechnen an.

Inhaltsübersicht

Steigungswinkel berechnen einfach erklärt

im Videozur Stelle im Video springen

Bei einer linearen Funktion $f(x) = m \cdot x +t$ kannst du stets den Steigungswinkel berechnen. Er gibt dir die Steigung in Grad an und ist definiert, als der positive Winkel, den die Gerade mit der x-Achse einschließt. Du musst zur Berechnung aber nicht den Schnittpunkt der Geraden mit der x-Achse kennen, sondern kannst stattdessen auch den Winkel $\alpha$ in jedem Steigungsdreieck betrachten.

Steigung Steigungsdreieck Steigungswinkel Gerade lineare Funktion — Steigungswinkel einer linearen Funktion

Um den Steigungswinkel zu berechnen, verwendest du immer eine dieser beiden Formeln:

Steigungswinkel berechnen Formel

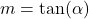$m = \tan(\alpha)$ oder $\alpha = \arctan(m)$

Dabei muss $\alpha \neq 90^{\circ}$ . Dabei ist der Arcustangens $\arctan(\alpha)$ gerade die Umkehrfunktion der Tangensfunktion $\tan(\alpha)$ .

Steigungswinkel berechnen – Gerade

im Videozur Stelle im Video springen

Wie du den Steigungswinkel berechnen kannst und auf welche Besonderheiten du bei bestimmten Geraden achten musst, zeigen wir dir hier. Dabei unterteilen wir in Geraden mit positiver und negativer Steigung:

Steigungswinkel berechnen: Gerade mit positiver Steigung

Für Geraden mit positiver Steigung siehst du die Situation oben im Bild dargestellt. Hast du hier die Funktionsgleichung $f(x) = \frac{2}{3}\cdot x -2$ gegeben, kannst du den Steigungswinkel berechnen mittels

$\alpha = \arctan\left(\frac{2}{3}\right) \approx 33,69^\circ.$

Anders herum kannst du, wenn du nur den Winkel $\alpha$ gegeben hast, daraus auch direkt die Steigung bestimmen und das Ergebnis graphisch überprüfen.

Beispiel 1

Gesucht ist die Funktionsgleichung einer linearen Funktion durch den Punkt P(2|1) mit dem Steigungswinkel $\alpha = 45^\circ$ . Die allgemeine Funktionsgleichung einer Geraden ist

$f(x) = m \cdot x +t,$

wobei wir die Steigung mit $\alpha = 45^\circ$ berechnen können als

$m = \tan(45^\circ) = 1.$

Jetzt müssen wir nur noch den y-Achsenabschnitt bestimmen. Dazu setzen wir und den Punkt P(2|1) ein

$1 = 1 \cdot 2 +t \quad \quad \quad \bigg| -2$

t = -1

Damit lautet die gesuchte Funktionsgleichung $f(x) = 1 \cdot x -1$ .

Steigungswinkel berechnen: Gerade mit negativer Steigung

Betrachten wir nun die fallenden Geraden, also diejenigen mit negativer Steigung, an einem Beispiel. Sei $f(x)=-0,5 \cdot x + 2,5$ . Wir versuchen, den Steigungswinkel $\alpha$ wie bisher zu berechnen

$\alpha = \arctan(-0,5) \approx -26,57^\circ$ .

Hier stoßen wir insofern auf ein Problem, dass die Größe eines Winkels nicht negativ sein kann!

Steigungswinkel negative Steigung Gerade — Steigungswinkel einer fallenden Gerade

Mit Blick auf den Funktionsgraphen siehst du sofort, dass wir hier nicht $\alpha$ (grün), sondern den türkisen Winkel $\alpha'$ berechnet haben. Um den grünen Winkel $\alpha$ zu berechnen, müssen wir daher zu $\alpha'$ noch $180^\circ$ addieren. Damit ergibt sich hier die Formel:

Steigungswinkel einer fallenden Gerade

$\alpha = \arctan(m)+180^\circ$ und $m = \tan(\alpha-180^\circ)$

Für unser Beispiel erhältst du somit den Winkel

$\alpha = \arctan(m)+180^\circ = -26,57^\circ + 180^\circ = 153,43^\circ.$

Sonderfälle

Einen Sonderfall beim Steigungswinkel berechnen stellen hier die waagerecht im Koordinatensystem liegenden Geraden dar. Sie haben die Steigung m=0 und daher die Funktionsgleichung f(x) = t . Wenn die Steigung Null ist, musst du nicht explizit den zugehörigen Steigungswinkel berechnen. Hier ist immer $\alpha = 0.$ Das siehst du auch direkt hier im Bild an der blauen Geraden.

waagrechte Gerade Senkrechte Gerade Steigung — Steigung einer waagrechten und senkrechten Geraden

Auch bei den senkrechten Geraden musst du vorsichtig sein. Sie stehen – wie du im Bild am Graphen der lilalen Geraden siehst – parallel zur y-Achse und haben somit einen Steigungswinkel von $90^\circ$ . Die Steigung kannst du aber nicht mit der Formel berechnen, da sie sozusagen „unendlich“ ist. Wenn du versuchst, $\tan(90^\circ)$ in deinen Taschenrechner einzugeben, wird er dir eine Fehlermeldung anzeigen. Das liegt daran, dass der Tangens definiert ist als

$\tan(\alpha) = \cfrac{\sin(\alpha)}{\cos(\alpha)}$

und $\cos(90^\circ) = 0$ ist. Du würdest somit „durch Null teilen“, was nicht erlaubt ist.

Schnittwinkel mit den Koordinatenachsen

im Videozur Stelle im Video springen

Beim Steigungswinkel berechnen, kannst du beispielsweise auch die Schnittwinkel der Funktion mit der x-Achse und mit der y-Achse bestimmen. Der Schnittwinkel bezeichnet immer den kleinsten Winkel, den zwei Geraden miteinander einschließen.

Betrachten wir zuerst die Schnittwinkel mit der x-Achse:

im Falle einer Geraden mit positiver Steigung ist das also gerade der Steigungswinkel $\alpha$ .
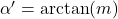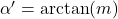bei einer Geraden mit negativer Steigung, haben wir bereits gesehen, dass wir mit der Formel $\alpha ' = \arctan(m)$ einen negativen Winkel erhalten. Jetzt interessieren wir uns aber für den im Bild orange eingezeichneten Winkel. Dieser ist gleich groß, wie $\alpha '$ , nur mit positivem Vorzeichen versehen. Du berechnest also wie gewohnt $\alpha ' = \arctan(m)$ und ignorierst das Minus.

Schnittwinkel Achsen Gerade Steigungswinkel — Schnittwinkel mit den Koordinatenachsen

Den Schnittwinkel $\beta$ mit der y-Achse kannst du leicht bestimmen, wenn du bedenkst, dass die y-Achse im $90^\circ$ -Winkel auf der x-Achse steht. Damit schließt $\alpha$ und $\beta$ mit dem Ursprung ein rechtwinkliges Dreieck ein, weswegen du $\beta$ über die Winkelsumme im Dreieck berechnen kannst. Es gilt

$180^\circ = 90^\circ + \alpha + \beta$

$\beta = 90^\circ - \alpha$ .

Diese Formel gilt sowohl für steigende als auch für fallende Gerade.

Beispiel 2

Gesucht sei der Winkel $\beta$ , den im obigen Bild die Gerade $f(x) = -0,5 \cdot x +2,5$ mit der y-Achse einschließt. Dazu bestimmen wir zuerst wie den orangen Winkel $\alpha = |\arctan(-0,5)| = 26,57^\circ$ . Mit der obigen Formel berechnen wir nun $\beta$ als $\beta = 90^\circ - 26,57^\circ = 63,43^\circ$ .

Quiz zum Thema Steigungswinkel

Beispiel Straße: Neigungswinkel berechnen

Eine klassische Anwendung ist beispielsweise die Berechnung des Bremswegs eines LKWs. Das schauen wir uns an einem Beispiel genauer an:

Auf einer Gebirgsstraße warnt ein Straßenschild vor einer Steigung von $20\%$ . Wir können die Straße näherungsweise als fallende Gerade darstellen und interessieren uns nun für ihren Steigungswinkel. Dazu müssen wir zuerst ihre Steigung bestimmen, indem wir die Prozentangabe $20\% = 0,2$ umrechnen. Für m = 0,2 berechnen wir nun $\alpha = \arctan(0,2) \approx 11,31^\circ$ .

zur Videoseite: Steigungswinkel

Beliebte Inhalte aus dem Bereich Funktionen

Schnittpunkte mit den Koordinatenachsen

Schnittpunkt zweier Geraden

Schnittpunkte zweier Funktionen

Schnittpunkt berechnen

Schnittwinkel berechnen

Steigungswinkel

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .