Steigung berechnen
Du willst wissen, was eine Steigung ist und mit welcher Formel du ganz leicht die Steigung einer Funktion berechnen kannst? Dann bist du hier genau richtig! Schau dir auch unser Video dazu an!
Inhaltsübersicht
Was ist eine Steigung?
Um eine Steigung zu berechnen, solltest du wissen, was eine Steigung überhaupt ist. Steigungen begegnen dir nämlich überall im Alltag.
Im Straßenverkehr geben dir zum Beispiel Verkehrsschilder an, wie groß die Steigung einer Straße ist. Auch beim Wandern interessiert es dich wahrscheinlich, welche Steigung der Berg hat, also wie steil er ist.
Wenn du zum Beispiel ein Gartenhaus baust, solltest du darauf achten, dass das Dach steil genug ist. Sonst kann Regenwasser nicht abfließen. Auch hier ist also die Steigung des Dachs von Bedeutung.
Aber welche Rolle spielen Steigungen in der Mathematik?
Steigung bestimmen bei Geraden
In der Mathematik kannst du mithilfe der Steigung die Steilheit von Geraden beschreiben. Je größer die Steigung, desto steiler ist die Gerade. Wenn die Steigung negativ ist, fällt die Gerade.
Wichtig: Anders als im Alltag unterscheidest du in der Mathematik meistens nicht zwischen Steigung und Gefälle! Ein Gefälle ist einfach eine negative Steigung. Der Begriff Steigung ist also immer richtig.
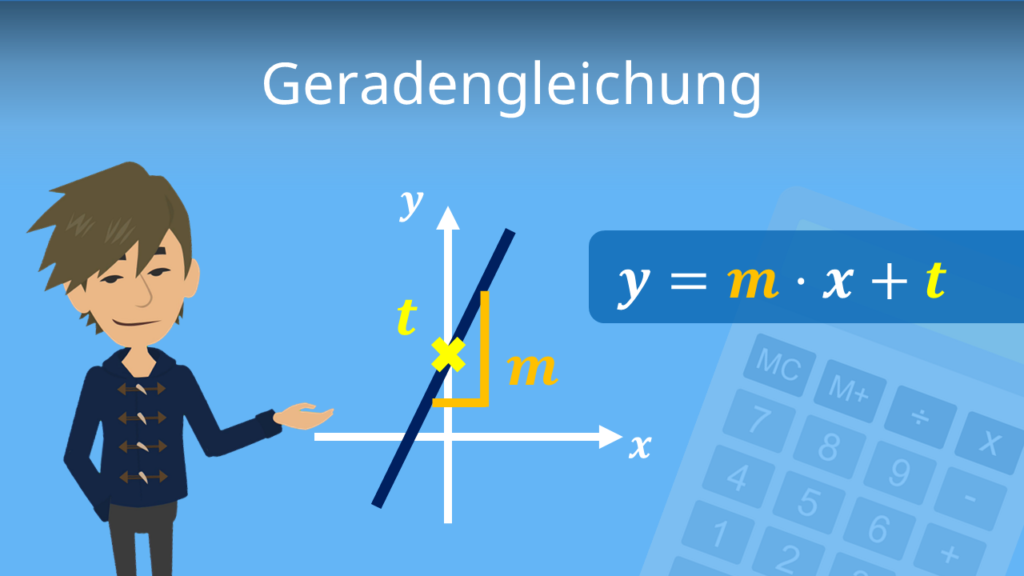
Mathematisch kannst du die Geraden durch eine Geradengleichung darstellen.
f(x) = mx + t
- wobei m die Steigung der Gerade ist
- und t der y-Achsenabschnitt
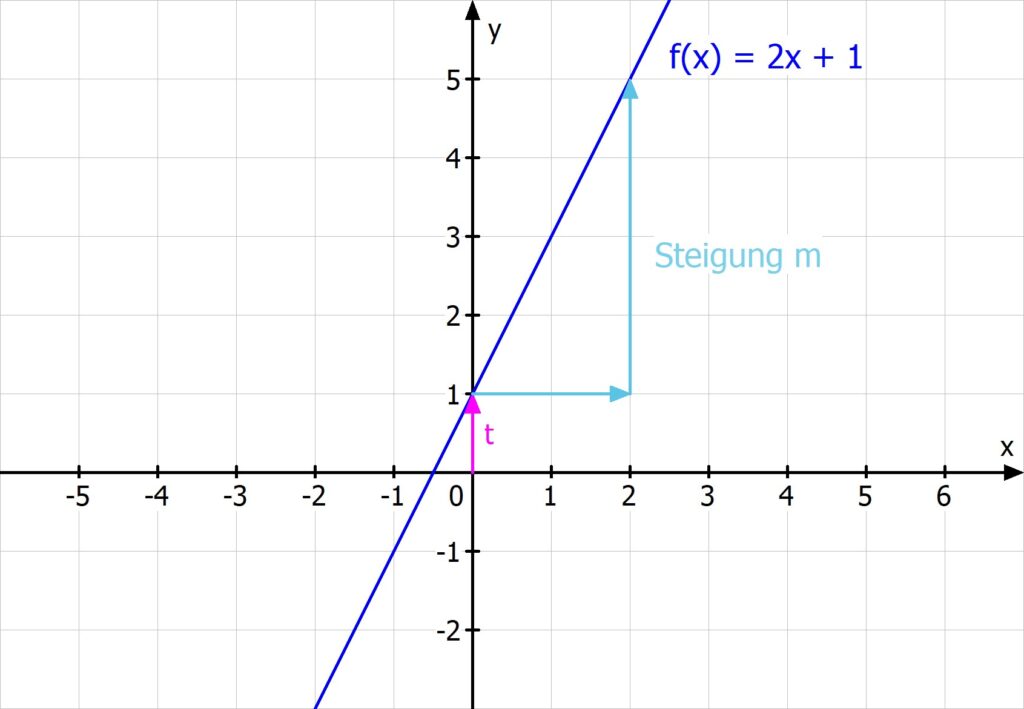
Wenn du deine Funktionsgleichung schon in der Form f(x) = mx + t gegeben hast, ist es ganz einfach, die Steigung abzulesen! Sie ist immer gleich m.
Bei der Funktion f(x) = 2x + 1 ist sie also gleich 2.
Übrigens: Hier lernst du, wie du die Steigung m bei linearen Funktionen berechnen kannst. Du kannst aber auch die Steigung von Funktionen ermitteln, die keine Geraden sind. Das machst du in der Kurvendiskussion. Schau dir unser Video an, um mehr darüber zu erfahren!
Bei Aufgaben zur Steigung kennst du oft entweder den Graph einer Funktion oder zwei Punkte auf dem Graphen. Du sollst dann meist:
- die Steigung am Graph ablesen
- die Steigung m berechnen mit Formel
- die Steigung in Prozent berechnen
- die Steigungswinkel berechnen
- die Gerade zeichnen
Schau dir die einzelnen Aufgabentypen gleich an!
Steigung am Graph ablesen
Aber was, wenn m nicht gegeben ist, und du die Steigung aus einem Graphen ablesen sollst? Dann hilft dir das sogenannte Steigungsdreieck , die Steigung m zu bestimmen!
Dabei gehst du so vor:
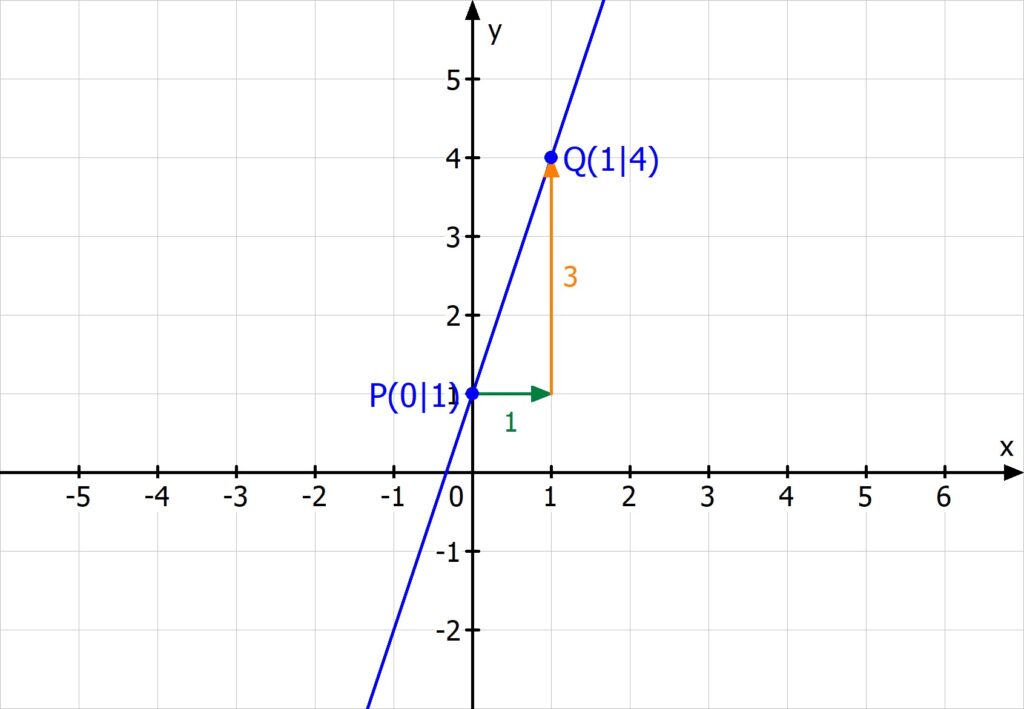
- Beginne dort, wo die Gerade die y-Achse schneidet. Das ist hier der Punkt P(0|1).
- Suche dir einen weiteren Punkt auf der Geraden, den du gut ablesen kannst, zum Beispiel Q(1|4).
- Gehe von deinem ersten Punkt so viele Einheiten waagrecht nach rechts, bis du einen geraden Strich zu deinem zweiten Punkt nach oben zeichnen kannst.
→ Hier musst du von P(0|1) nur um 1 Kästchen nach rechts. - Wenn du dann einen geraden Strich um 3 Kästchen nach oben zeichnest, landest du bei dem Punkt Q(1|4).
Teile nun die Anzahl an Kästchen, die du nach oben gegangen bist, durch die Anzahl der Kästchen, die du nach rechts gegangen bist. Hier rechnest du also:
![Rendered by QuickLaTeX.com \[m = \frac{\textcolor{orange}{3}}{\textcolor{teal}{1}} = 3\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-7dfc26b04de99a2058d16f4f26475510_l3.png)
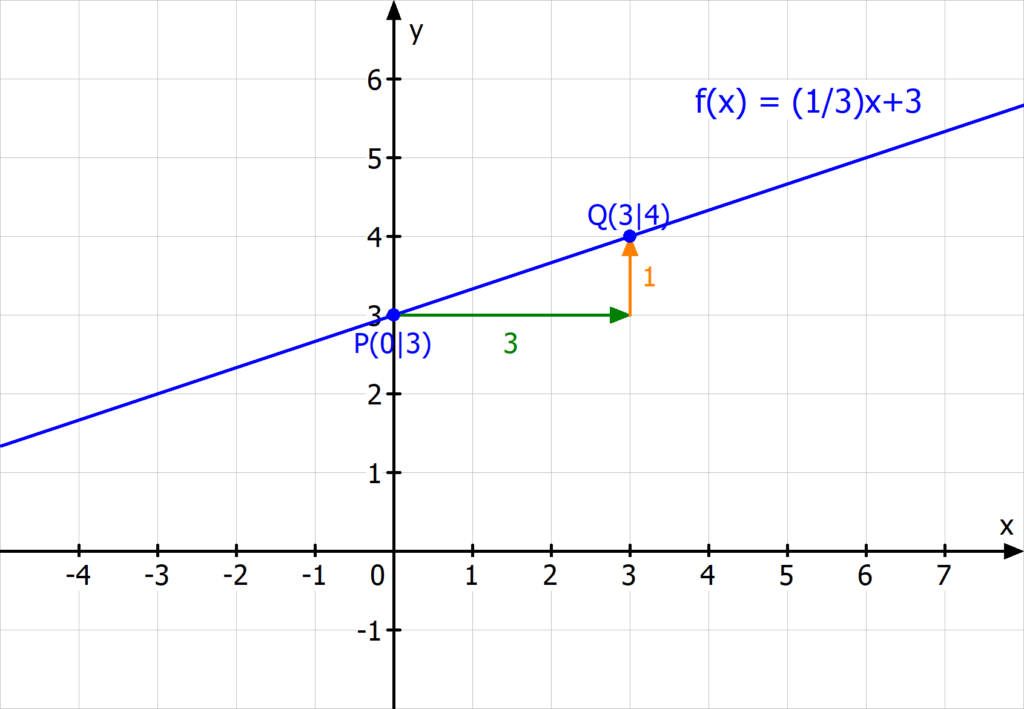
Manchmal musst du aber auch mehr als 1 Kästchen nach rechts gehen:
In diesem Fall gehst du also für das Steigungsdreieck 3 Einheiten nach rechts und 1 Einheit nach oben gehen. Deshalb rechnest du:
![Rendered by QuickLaTeX.com \[\textcolor{teal}{m} = \frac{\textcolor{orange}{1}}{\textcolor{olive}{3}}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-5a6f0c0efa24478438eff18b42ab2c10_l3.png)
Bei Geraden mit negativer Steigung gehst du genauso vor. Auch hier läufst du zunächst vom Schnittpunkt mit der y-Achse nach rechts. Dieses Mal gehst du danach aber nach unten, bis du die Gerade triffst. Vor dein m schreibst du dann ein minus.
Übrigens: Du kannst auch mit einem beliebigen Punkt auf der Geraden anfangen und von dort aus 1 nach rechts gehen. Dann zählst du, wie viele Schritte du nach oben oder unten gehen musst, um wieder auf der Geraden zu landen. Die Anzahl der Schritte ist deine Steigung.
Gar nicht so schwer, oder? Dann schau dir jetzt an, wie du mit der Steigungsformel Steigungen bestimmen kannst!
Steigung berechnen einfach erklärt — Steigungsformel
Manchmal sollst du m aber nicht am Graphen ablesen, sondern mit einer Formel berechnen.
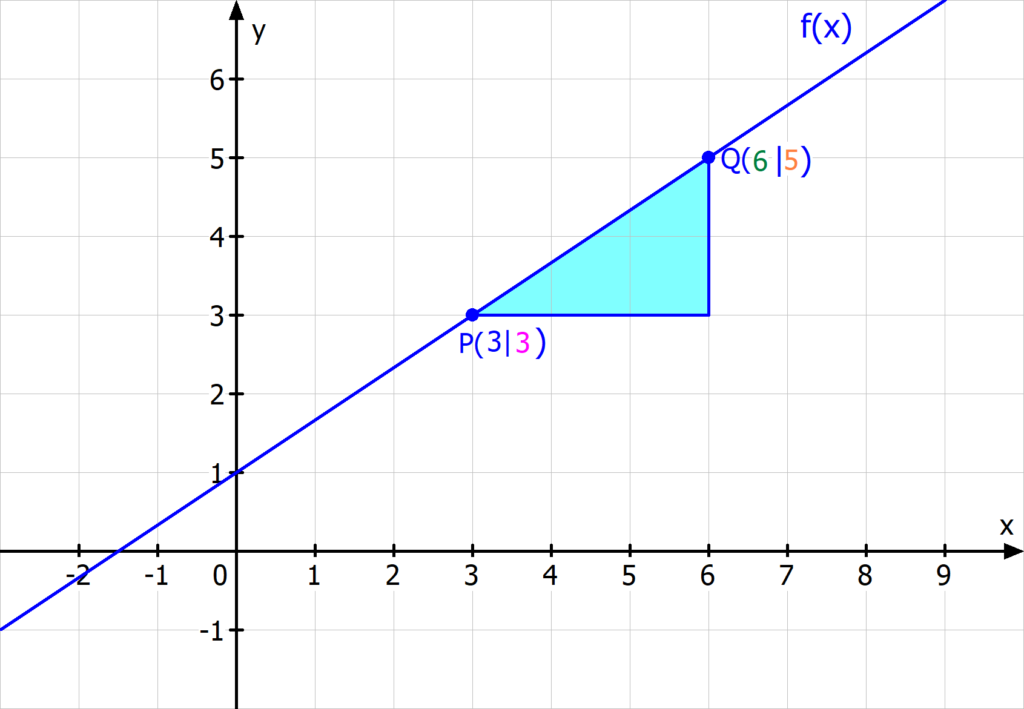
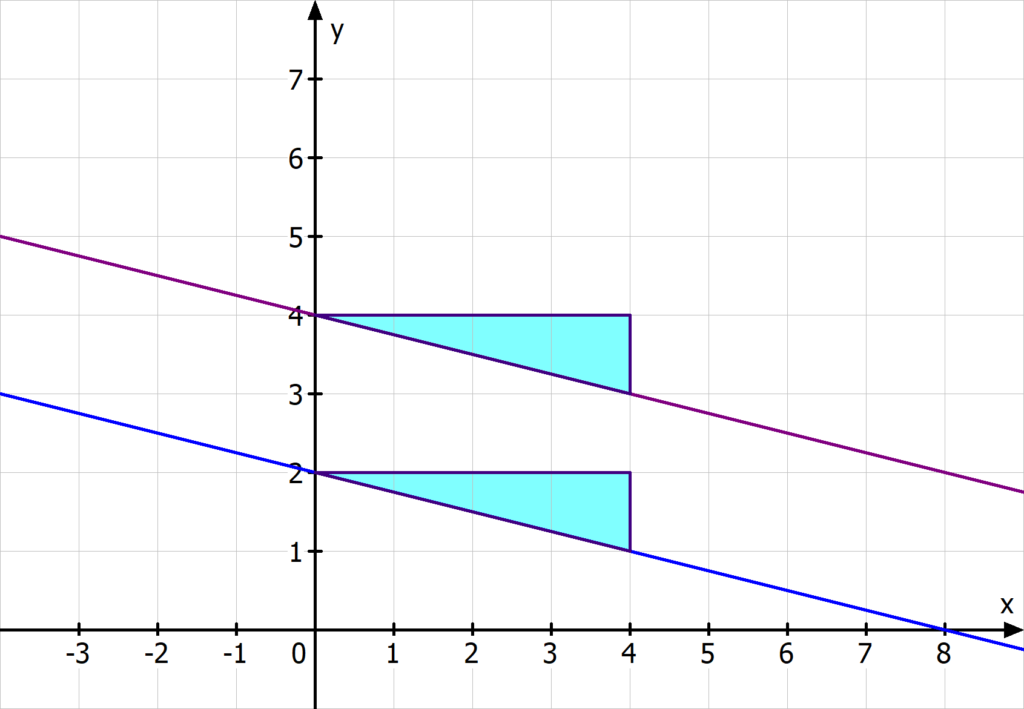
Du hast die Punkte P(3|3) und Q(6|5) gegeben und sollst m rechnerisch bestimmen.
Dazu gehst du in 3 Schritten vor:- Berechne y2–y1. Hier sind das 5–3, also 2.
- Berechne x2–x1. Hier sind das 6–3, also 3.
-
Teile (y2–y1) durch (x2–x1). Du erhältst also m =
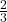
Wenn du die Steigung graphisch über das Steigungsdreieck bestimmst, kommst du übrigens zu dem gleichen Ergebnis! Denn du gehst erst 3 nach rechts und dann 2 nach oben, um von einem Punkt zum anderen zu kommen.
Die Steigung m kannst du mithilfe des Differenzenquotienten aus zwei verschiedenen Punkten P(x1|y1) und Q(x2|y2) auf der Geraden berechnen.
m = Δy/Δx = (y2–y1) / (x2–x1)
Steigung in Prozent berechnen
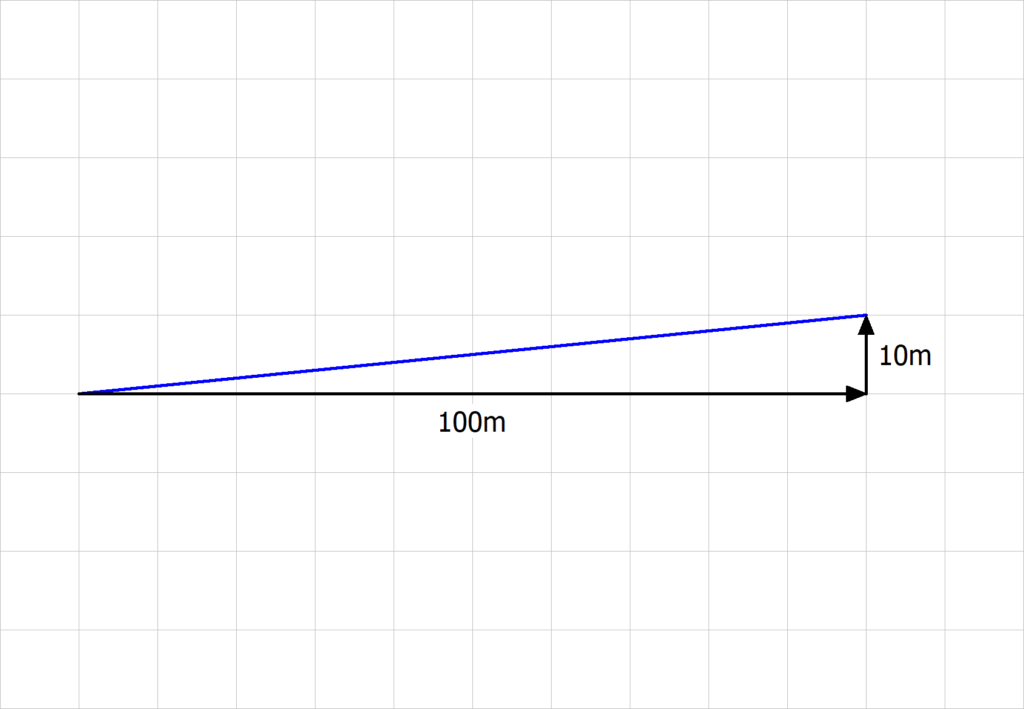
Erinnerst du dich noch an das Verkehrsschild?
Es hat auf einen Anstieg von 10 % hingewiesen. Das bedeutet, dass pro 100 m waagrechter Strecke die Höhe um 10 m zunimmt.
Um den Anstieg oder das Gefälle als prozentuale Steigung mit einer Formel zu berechnen, gehst du also vor wie bisher und teilst den Höhenunterschied durch die waagrechte Strecke. Anschließend musst du deinen Bruch nur noch in Prozent umrechnen . Dazu multiplizierst du mit 100.
![Rendered by QuickLaTeX.com \[\frac{\text{\textcolor{orange}{Höhenunterschied}}}{\text{\textcolor{teal}{waagrechte Strecke}}} \cdot 100 = \frac{\textcolor{orange}{10}}{\textcolor{teal}[100}} \cdot 100 = 10\%\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-2ca79000685436b980742385d92b1e90_l3.png)
Manchmal hast du aber auch in einer Textaufgabe das Gefälle in Prozent gegeben und sollst daraus m bestimmen. Wenn dabei von Gefälle gesprochen wird, ist die Steigung negativ. Steht auf einem Verkehrsschild also, dass ein Abhang ein Gefälle von 20 % aufweist, dann ist m = -0.2.
Übrigens: Hat ein Wanderweg eine Steigung von 100 %, so hat er die Steigung m = 1. Die Strecke verläuft also nicht senkrecht, sondern in einem 45º Winkel.
Um die Steigung in Prozent zu berechnen, teilst du den Höhenunterschied (z.B. Höhenmeter auf einer Wanderung) durch die waagrechte Strecke. Steigt ein Weg zum Beispiel 15m pro 300m, dann ist seine Steigung (15m : 300m) · 100 = 5 %
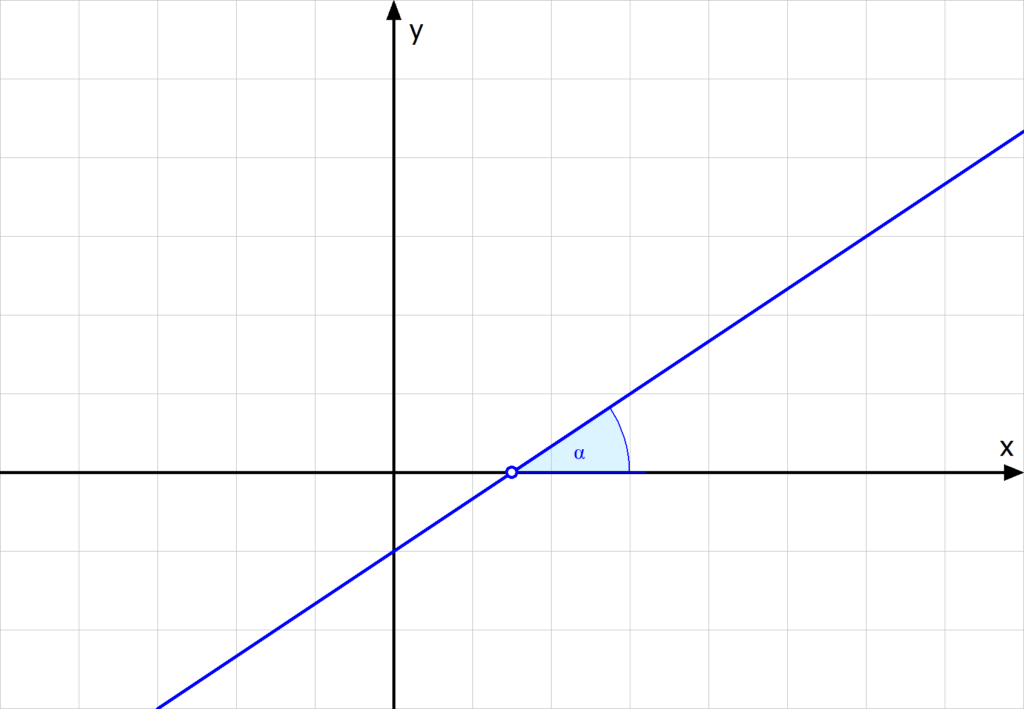
Steigungswinkel
Der Steigungswinkel α gibt an, in welchem Winkel eine Gerade zur x-Achse steht.
Bei einer Geradengleichung der Form f(x) = mx + b gilt:
m = tan(α)
α = tan-1(m)
Hast du zum Beispiel die Gerade f(x) = 2x + 3, dann ist der Steigungswinkel α = tan-1(2) ≈ 63°
Eine ausführlichere Erklärung mit vielen Beispielen zum Steigungswinkel findest du hier .
Gerade zeichnen
Du kennst die Funktionsgleichung f(x) = mx + t einer Geraden und sollst sie in ein Koordinatensystem einzeichnen? Schau dir die einzelnen Schritte dazu am Beispiel f(x) = ¾x + 2 an:
- Markiere die Zahl 2 auf der y-Achse.
- Gehe von dort aus so viele Kästchen nach rechts wie der Nenner von m (Zahl oben im Bruch). Hier läufst du also 4 Kästchen nach rechts.
- Gehe von dort aus so viele Kästchen nach oben (falls m > 0) oder nach unten (falls m < 0) wie der Zähler von m (Zahl unten im Bruch). Hier gehst du also 3 Kästchen nach oben.
- Du erhältst einen Punkt. Verbinde ihn mit der 2 auf der y-Achse.
Fertig! Schon hast du deine Gerade gezeichnet!
Merke: Wenn m kein Bruch ist, sondern zum Beispiel m = 5, dann ist der Nenner immer 1. Der Zähler ist dann einfach das m.
Bedeutung der Steigung
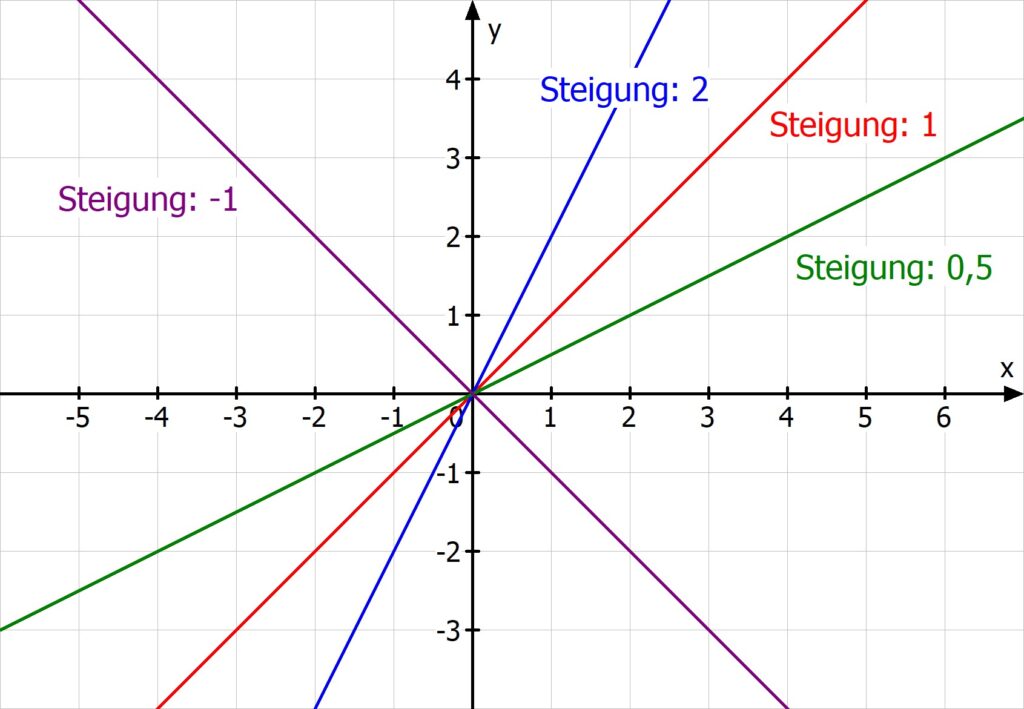
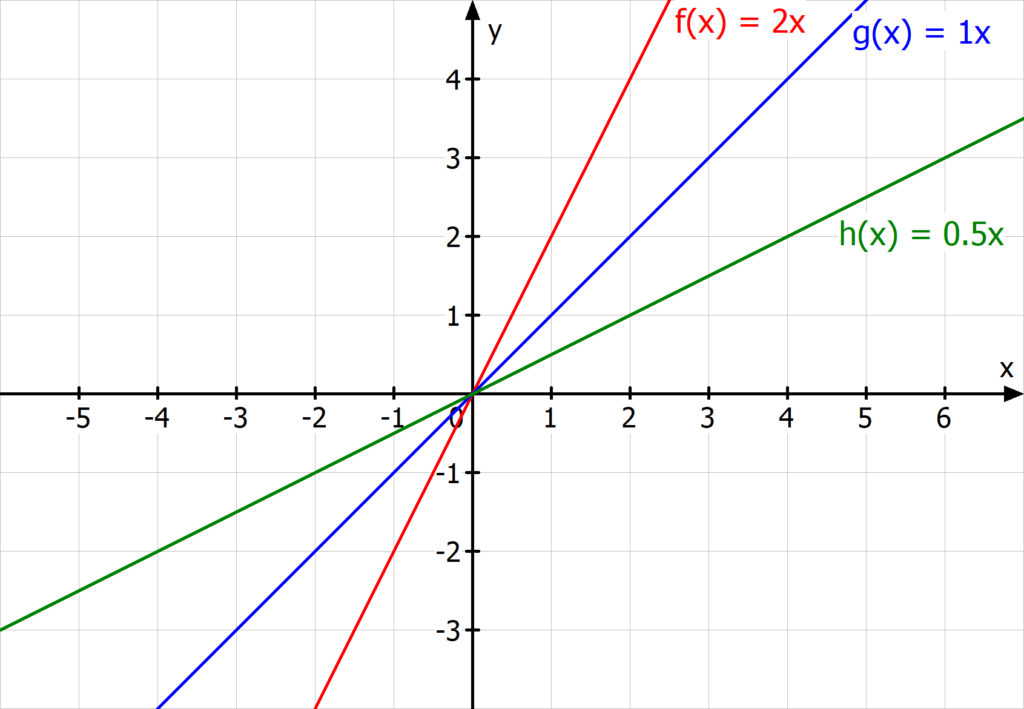
Unterschiedliche Steigungen führen zu unterschiedlichen Geraden. Den Einfluss der Größe von m kannst du am besten auf diesem Bild sehen:
Du siehst: Die Gerade mit dem größten m — hier f(x) = 2x — ist am steilsten.
Allgemein hat eine Gerade die Gleichung y = mx + t. Die Steigung m legt fest, wie stark sich die Funktionswerte (y-Werte) des Graphen ändern, wenn du den x-Wert änderst.
Je größer m, desto steiler die Gerade. Hat m ein negatives Vorzeichen, ist sie dabei nach unten geneigt.
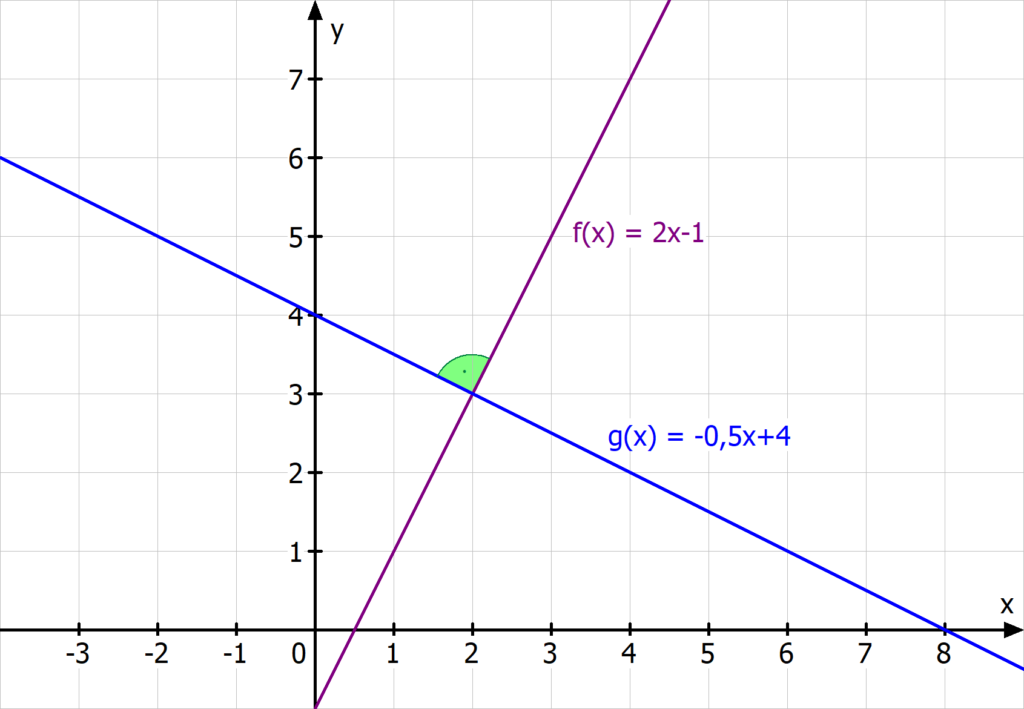
Parallele und senkrechte Geraden
Parallele Geraden haben immer die gleiche Steigung. Das ist auch der Grund dafür, dass sie sich nie schneiden.
Senkrechte Geraden schneiden sich in einem 90º Winkel. Für die Geraden gilt dann
![Rendered by QuickLaTeX.com \[f(x) = \textcolor{teal}{m} \cdot x +t_1\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-51e49e8629caaa3953f931080aeacedb_l3.png)
![Rendered by QuickLaTeX.com \[g(x) = \textcolor{teal}{-\frac{1}{m}} \cdot x + t_2\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-7aa3d721a5d38d161b89c6412328f0d9_l3.png)
Hat die Funktion f(x) also die Steigung 2, muss die Funktion g(x) ein Gefälle von 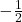 = -0.5 haben, um senkrecht zu f(x) zu sein.
= -0.5 haben, um senkrecht zu f(x) zu sein.
Das kannst du auch auf diesem Bild leicht erkennen:
Übrigens: Wie du den Schnittpunkt der Geraden berechnen kannst, zeigen wir dir hier .
Steigung berechnen — häufige Fragen
-
Was ist die Steigung?
Die Steigung gibt an, wie steil etwas steigt oder fällt. Im Alltag interessiert dich die Steigung zum Beispiel bei Bergwanderungen. In der Mathematik kannst du die Steigung m einer Funktion berechnen. Sie ist hier ein Maß für die Steilheit von Geraden.
-
Wie kann ich die Steigung bestimmen?
Wenn du zwei Punkte auf einer Geraden kennst, kannst du ein Steigungsdreieck zwischen ihnen einzeichnen. Die Steigung ist dann die senkrechte Seite des Dreiecks (Gegenkathete) durch die waagrechte Seite (Ankathete). Sie ist positiv, wenn deine Gerade steigt und negativ, wenn sie fällt.
-
Was bedeutet 15 % Steigung?
Siehst du auf einem Verkehrsschild 15 % Steigung, heißt das, dass die Straße pro 100 Meter um 15 Meter ansteigt oder abfällt. Du hast also 15 Meter Höhenunterschied auf 100 Metern.
Geradengleichung
Super, jetzt weißt du, wie du die Steigung einer Geraden bestimmst: Du kannst die Steigung berechnen, indem du die Formel anwendest oder sie mithilfe des Steigungsdreiecks bestimmst. Außerdem hast du gesehen, dass sie immer in der Geradengleichung vorkommt. Du willst wissen, was du sonst noch alles brauchst, um eine Geradengleichung aufzustellen? Dann schau dir doch einfach unser Video dazu an.