y = mx + b
Du hast die Formel y = mx + b vor dir liegen und weißt nicht, was du damit anfangen sollst? In diesem Beitrag erfährt du alles, was du dazu wissen musst. Schau dir auch unser Video dazu an!
Inhaltsübersicht
y = mx + b einfach erklärt
Die Gleichung y = mx + b beschreibt eine Gerade. Das m steht für die Steigung und das b steht für den y-Achsenabschnitt. Die Gerade y = 2x + 1 hat zum Beispiel eine Steigung von 2 und schneidet die y-Achse bei 1. Um b und m zu berechnen, benötigst du zwei beliebige Punkte auf der Geraden.
Für x kannst du Zahlen in die Gleichung einsetzen und dann einen passenden y-Wert berechnen. Zusammen ergeben x und y einen Punkt P(x|y) auf der Geraden.
Vielleicht kennst du die Formel y = mx + b auch als y = mx + c oder y = mx + n. An der Rechenweise ändert sich nichts, außer dass du anstatt b ein c oder n schreibst.
Hast du schonmal die Gleichung f(x) = mx + b gesehen? Das ist das Gleiche wie y = mx + b.
Wie bestimmst du y = mx + b mit zwei Punkten?
Du hast eine Aufgabe vor dir liegen, bei der du m und b bestimmen musst? Wenn du dafür zwei Punkte P1 (2|1) und P2 (3|0) gegeben hast, kannst du nach dieser Anleitung vorgehen:
1. Schritt: Die Steigung m berechnen.
m =  = -1
= -1
Übrigens: Eine 1 oder -1 kann vor dem x wegfallen, sodass nur noch x oder –x da steht. Aktuell sieht deine Geradengleichung also so aus: y = –x + b.
Du berechnest die Steigung m, wenn du die Punkte P1 (x1|y1) und P2 (x2|y2) gegeben hast, mit folgender Formel:
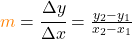
2. Schritt: Den Schnittpunkt mit der y-Achse berechnen.
Du kannst dafür einfach einen der beiden gegebenen Punkte, beispielsweise P1 (2|1), in die Geradengleichung y = –x + b einsetzen. Für x setzt du die 2 ein und für y die 1.
y = –x + b | Punkt P1 (2|1) einsetzen
1 = (-1) · 2 + b
1 = -2 + b
Was dir jetzt noch fehlt ist das Umstellen der Gleichung . Um -2 auf die andere Seite zu bringen, rechnest du +2 auf beiden Seiten dazu.
1 = -2 + b | +2
1 + 2 = -2 + 2 + b
3 = b
3. Schritt: Am Ende fügst du nur noch beide Ergebnisse in die Geradengleichung ein:
y = –x + 3
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Wie bestimmst du y = mx + b mit einem Punkt?
Es kann passieren, dass du bei einer Aufgabe nur einen Punkt P gegeben hast. Wie kannst du dann trotzdem die fehlenden Werte für die Gleichung bestimmen?
Das geht nur, wenn du entweder den y-Achsenabschnitt b oder die Steigung m bereits kennst. Dann musst du nicht mehr beide Werte berechnen. Wie du in den einzelnen Fällen vorgehen kannst, zeigen wir dir jetzt.
1. Fall: Ein Punkt A und y-Achsenabschnitt b gegeben
A (3|5), b = -1
1. Schritt: Die gegebene Zahl für b in die Geradengleichung y = mx + b einsetzen.
y = mx + (-1)
y = mx – 1
2. Schritt: Punkt A (3|5) einsetzen und die Geradengleichung nach m umstellen.
Für x setzt du 3 ein und für y setzt du 5 ein.
y = mx – 1 | Punkt A (3|5) einsetzen
5 = m · 3 – 1 | +1
5 + 1 = m · 3 – 1 + 1
6 = m · 3 | : 3
2 = m
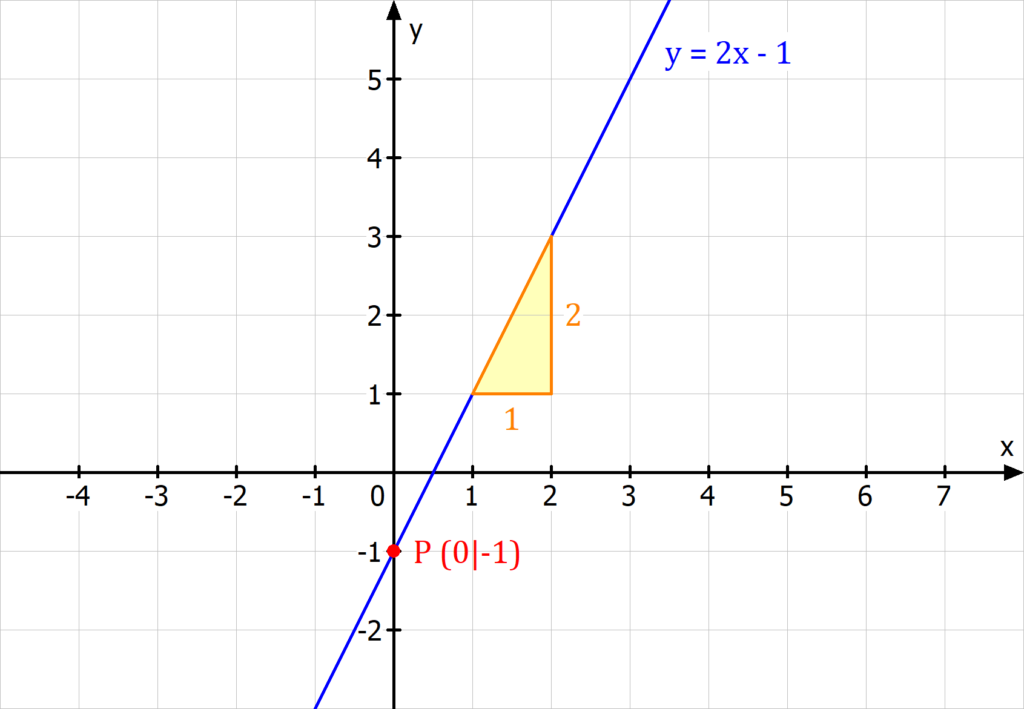
3. Schritt: Jetzt fügst du nur noch m in die Geradengleichung ein: y = 2x – 1.
Prima! Du hast die Geradengleichung erfolgreich berechnet.
2. Fall: Ein Punkt B und Steigung m gegeben
B (-1|4), m = 2
1. Schritt: Die Zahl für m in die Geradengleichung y = mx + b einsetzen.
y = 2x + b
2. Schritt: Den Punkt B (-1|4) einsetzen und die Geradengleichung nach b umstellen. Für x setzt du -1 ein und für y setzt du 4 ein.
y = 2x + b | Punkt B (-1|4) einsetzen
4 = 2 · (-1) + b
4 = -2 + b | +2
6 = b
3. Schritt: Jetzt fügst du nur noch b ein und schon hast du die fertige Geradengleichung: y = 2x + 6.
Streng genommen ist dieses Beispiel der 2. Schritt aus dem Kapitel „Wie bestimmst du y = mx + b mit zwei Punkten?“. Da wird, nachdem du die Steigung m mit einer Formel berechnet hast, auch ein Punkt eingesetzt und nach b umgestellt.
Wie liest du y = mx + b aus einem Graphen ab?
Wenn du nur einen Graphen gegeben hast, dann kannst du daraus auch den y-Achsenabschnitt b und die Steigung m für die Geradengleichung y = mx + b ablesen.
Den y-Achsenabschnitt b erkennst du an dem Schnittpunkt mit der y-Achse. Im Beispiel ist das P (0|2) und deswegen b = 2.
Die Steigung kannst du mithilfe eines Steigungsdreiecks ablesen. Du nimmst dir einen Punkt auf der Geraden und gehst von dort aus so viele Kästchen nach rechts (Im Beispiel: 2) und nach oben (Im Beispiel: 1) bis du wieder auf einem Punkt auf der Geraden landest. Dabei entsteht ein Dreieck. Die Länge, die du nach oben gegangen bist, musst du durch die Länge, die du nach rechts gegangen bist, teilen: m = 1 : 2 = 0,5.
Jetzt fügst du nur noch m und b in die Geradengleichung ein: y = 0,5x + 2
y = mx + b — häufigste Fragen
(ausklappen)
y = mx + b — häufigste Fragen
(ausklappen)-
Was sagen m und b in y = mx + b aus?In der Gleichung
 ist
ist  die Steigung der Geraden und
die Steigung der Geraden und  der y-Achsenabschnitt (Schnittpunkt mit der y-Achse). Konkret bedeutet das:
der y-Achsenabschnitt (Schnittpunkt mit der y-Achse). Konkret bedeutet das:  zeigt, ob die Gerade steigt oder fällt, und
zeigt, ob die Gerade steigt oder fällt, und  ist der y-Wert bei
ist der y-Wert bei  .
.
-
Wie berechne ich die Steigung m aus zwei Punkten?Die Steigung
 berechnest du aus zwei Punkten
berechnest du aus zwei Punkten  und
und  mit
mit  . Zum Beispiel gilt für
. Zum Beispiel gilt für  und
und  :
:  .
.
-
Wie berechne ich den y-Achsenabschnitt b mit einem Punkt?Den y-Achsenabschnitt
 berechnest du mit einem Punkt nur dann, wenn die Steigung
berechnest du mit einem Punkt nur dann, wenn die Steigung  schon bekannt ist: Setze den Punkt
schon bekannt ist: Setze den Punkt  in
in  ein und stelle nach
ein und stelle nach  um. Beispiel: Bei
um. Beispiel: Bei  und
und  gilt
gilt  , also
, also  .
.
-
Wann reicht ein Punkt aus, um y = mx + b zu bestimmen?Ein Punkt reicht aus, um
 zu bestimmen, wenn zusätzlich entweder die Steigung
zu bestimmen, wenn zusätzlich entweder die Steigung  oder der y-Achsenabschnitt
oder der y-Achsenabschnitt  bereits gegeben ist. Dann setzt du den Punkt in die Gleichung ein und stellst nach der fehlenden Größe um, statt beide Werte berechnen zu müssen.
bereits gegeben ist. Dann setzt du den Punkt in die Gleichung ein und stellst nach der fehlenden Größe um, statt beide Werte berechnen zu müssen.
-
Wie lese ich m und b aus einem Graphen ab?Aus einem Graphen liest du
 am Schnittpunkt der Geraden mit der y-Achse ab. Die Steigung
am Schnittpunkt der Geraden mit der y-Achse ab. Die Steigung  bestimmst du mit einem Steigungsdreieck: Gehe von einem Punkt auf der Geraden Kästchen nach rechts und nach oben bis zum nächsten Punkt und rechne
bestimmst du mit einem Steigungsdreieck: Gehe von einem Punkt auf der Geraden Kästchen nach rechts und nach oben bis zum nächsten Punkt und rechne  . Beispiel: 2 nach rechts und 1 nach oben ergibt
. Beispiel: 2 nach rechts und 1 nach oben ergibt  .
.
Lineares Gleichungssystem
Eine Geradengleichung mit zwei Punkten kannst du auch mithilfe eines linearen Gleichungssystems lösen. Wie das funktioniert, erfährst du in diesem Video !