Polynom
Hier erfährst du, was ein Polynom ist und welche Eigenschaften es hat. Außerdem findest du viele Beispiele und ein verständliches Video zum Thema.
Inhaltsübersicht
Was ist ein Polynom?
Der Ausdruck Polynom klingt zwar im ersten Moment kompliziert, tatsächlich bezeichnet er aber nur eine bestimmte Art mehrgliedriger Terme. Beispiele dafür sind etwa
a+b+c
10x5-x+3x3+4
3x2-8x+2
Ein Polynom besteht aus Variablen, zwischen denen Plus- oder Minuszeichen stehen. Die Variablen besitzen oft
- einen Vorfaktor, also eine Zahl, mit dem die Variable multipliziert wird. Er steht vor der Variable.
- eine Hochzahl oder Potenz, die eine natürliche Zahl ist.
Eigentlich zählst du bei einem Polynom also nur Potenzfunktionen zusammen oder ziehst sie voneinander ab.
Eigenschaften von Polynomen
Die einzelnen Teile eines Polynoms und seine Eigenschaften erkennst du schnell an diesem Beispiel:
x2+3x-1
Variablen
Variablen werden mit Buchstaben beschrieben. Meistens sind das x oder x1 , x2 , x3 usw.
- Das Polynom (x2+3x-1) enthält nur eine Variable: x
Vorfaktoren/Koeffizienten
Vorfaktoren oder Koeffizienten sind die Zahlen, die vor einer Variable stehen. Du musst die Variable immer mit dem Vorfaktor multiplizieren.
- Die Vorfaktoren des Polynoms (1x2+3x-1) sind 1 , 3 und -1
- Wenn vor einer Variable kein Vorfaktor steht (wie bei x2), dann muss man sich eine 1 dazu denken, denn 1*x2=x2
- Vorfaktoren werden auch Koeffizienten genannt
Potenzen
Potenzen sind die Hochzahlen über den Variablen. Du multiplizierst eine Variable so oft mit sich selbst, wie ihre Hochzahl angibt. x2 ist also x*x.
- Die Potenzen des Polynoms (x2+3x1-1x0) sind 2, 1 und 0
- Steht eine Variable ohne Potenz da (wie bei 3x), dann muss man sich eine 1 als Potenz dazu denken (denn x1=x)
- Steht ein Vorfaktor ohne Variable da (wie bei -1), dann muss man sich als Potenz eine 0 dazu denken (denn x0=1)
Glieder
Die einzelnen Summenteile werden Glieder genannt.
- x2, 3x und -1 sind die Glieder des Terms (x2+3x–1).
Keine Polynome sind alle komplizierteren Terme, die beispielsweise Wurzeln oder Brüche enthalten, deren Nenner aus einer Variable besteht (gebrochen rationale Funktionen ).

-
 .
.
 statt
statt  .
.Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Grad eines Polynoms
Der Grad eines Polynoms ist immer die höchste Potenz des Polynoms. Es ist also die Hochzahl bei einer Variablen, die am größten ist. Hier findest du einige Beispiele für den Grad verschiedener Polynome:
- –4x3+2x2+3x-1 Polynom 3. Grades (wegen 4x3)
- -7x5-2x3+12 Polynom 5. Grades (wegen -7x5)
- -7x-2x2+12 Polynom 2. Grades (wegen 2x2)
Allgemeines Polynom
Mit die wichtigsten Polynome sind diejenigen mit nur einer Variablen x. Man bezeichnet sie auch als „Polynome in einer Variablen x“. Allgemein aufgeschrieben sehen sie so aus:

Beispiele für Polynome in einer Variablen x
- -2x3+12x2+3x-1
- 8x5-2x3
- x8+3x5-16x2
Nullpolynom
Das denkbar einfachste Polynom heißt Nullpolynom. Es ist konstant Null
f(x)=0.
Der Grad des Nullpolynoms ist auf -1 oder  festgelgt. Sein Funktionsgraph ist identisch zur x-Achse, das heißt es handelt sich dabei um eine waagrechte Gerade im Koordinatensystem mit y-Achsenabschnitt
festgelgt. Sein Funktionsgraph ist identisch zur x-Achse, das heißt es handelt sich dabei um eine waagrechte Gerade im Koordinatensystem mit y-Achsenabschnitt  .
.
Monom
Ein Monom besteht aus nur einem Glied. Beispiele hierfür sind:
- a


Binom
Ein Binom besteht immer aus zwei Gliedern, es ist die Summe oder die Differenz zweier Monome. Typische Beispiele für ein solches Binom sind
- a+b
- 2x2+x

- 4ab-b.
Achtung: Pass auf, dass du das Binom nicht mit den binomischen Formeln verwechselst! Hier werden zwei Binome multipliziert!
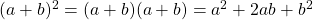
Trinom
Ein Trinom besteht im Gegensatz zum Binom aus drei einzelnen Termen, beziehungsweise aus drei Monomen. Typische Beispiele dafür sind
- a+b+c
- 2x+3-y
- ax2+bx+c
- a2+2ab+b2.
Polynomdivision
Polynome kannst du auch durcheinander teilen. Das funktioniert im Prinzip genauso wie das schriftliche Teilen in der Grundschule. Möchtest du etwa das Polynom 5x2+3x-12 durch das andere Polynom x-4 teilen, dann würde das Ganze so aussehen:
Die Polynomdivision musst du unbedingt können um Nullstellen von Polynomen dritten Grades oder höher, zu bestimmen. Wie das geht erklären wir natürlich ausführlich in einem eigenem Video dazu. Schau es dir gleich an!

