Natürlicher Logarithmus
Ob natürlicher Logarithmus oder Logarithmus naturalis, hier erfährst du alles Wichtige zum ln x! Du möchtest dich beim Lernen lieber entspannt zurücklehnen? Dann schau dir jetzt unser Video zum natürlichen Logarithmus an!
Inhaltsübersicht
Natürlicher Logarithmus einfach erklärt
Der natürliche Logarithmus ist eigentlich nur ein Spezialfall vom allgemeinen Logarithmus . Er hat als sogenannte Basis die Eulersche Zahl e. Er wird als ln geschrieben.

Du kennst bei solchen Aufgaben also schon das Ergebnis y und die Basis e und suchst jetzt nur noch den Exponenten x.

Das x ist also gerade die Zahl, die dir anzeigt, wie oft du e mal e rechnen musst, um zum gegebenen Ergebnis y zu kommen. Das e steht dabei für die Eulersche Zahl.

Hinweis: Dein Taschenrechner hat eine extra Taste für den natürlichen Logarithmus ln x.
Natürlicher Logarithmus berechnen
Der natürliche Logarithmus wird auch als Logarithmus naturalis bezeichnet. Damit kannst du alle Gleichungen lösen, bei denen du dich fragst, welche Zahl x du in den Exponenten von e nehmen musst, um eine andere Zahl y zu erhalten.


Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Beispiel 1
Betrachte die Gleichung
 .
.
Das x kannst du nun ganz einfach mit dem natürlichen Logarithmus berechnen.

Beispiel 2
Angenommen du willst wissen, welche Zahl x du in den Exponenten von e nehmen musst, um als Ergebnis den Potenzwert 21 zu erhalten. Dieses Problem kannst du dann als Gleichung formulieren.

Um das x zu berechnen, nutzt du jetzt den natürlichen Logarithmus. Du wendest auf beide Seiten den natürlichen Logarithmus an.

Das kannst du nun umformen.
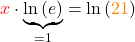

Dafür nutzt du die Taste auf deinem Taschenrechner und setzt entsprechend die 21 ein.
Hinweis: Den natürlichen Logarithmus kannst du auch als eine Funktion betrachten. Alles Wichtige zur ln Funktion haben wir in einem extra Video für dich zusammengefasst.
Sonderfall
Der ln 1 ist eine besondere Stelle. Hier ist der natürliche Logarithmus nämlich gerade Null.

Erinnere dich an die Potenzgesetze, besonders an die Regel x0=1. Eine Zahl hoch Null ergibt also Eins. Das gilt dann auch, wenn du die Eulersche Zahl e als Basis nimmst.

Deshalb ist auch der ln 1 gleich Null, denn die Null ist gerade die Zahl, die du in den Exponenten von e schreiben musst, um Eins zu erhalten.
Natürlicher Logarithmus Regeln
Für den natürlichen Logarithmus gibt es ein paar Rechenregeln, die du kennen solltest.


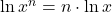
![Rendered by QuickLaTeX.com \ln \sqrt[n]{x}=\frac{1}{n} \ln x](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-cc6886f61c031ea8104c1de075414390_l3.png)
Viele Beispiele dazu findest du auch in unserem extra Video zu den ln Regeln .
Natürlicher Logarithmus Aufgaben
Jetzt kannst du den natürlichen Logarithmus anwenden. Hier findest du nochmal zwei Aufgaben zum Üben.
a) 
b) 
Natürlicher Logarithmus — häufigste Fragen
(ausklappen)
Natürlicher Logarithmus — häufigste Fragen
(ausklappen)-
Was bedeutet der natürliche Logarithmus ln in einfachen Worten?Der natürliche Logarithmus
 bedeutet: Er gibt dir den Exponenten an, den die Eulersche Zahl
bedeutet: Er gibt dir den Exponenten an, den die Eulersche Zahl  haben muss, um eine Zahl
haben muss, um eine Zahl  zu ergeben. Anders gesagt:
zu ergeben. Anders gesagt:  ist genau das
ist genau das  , für das
, für das  gilt.
gilt.
-
Wie hilft mir ln beim Lösen von Gleichungen mit e hoch x?
 hilft dir, weil es bei Gleichungen der Form
hilft dir, weil es bei Gleichungen der Form  direkt den Exponenten liefert:
direkt den Exponenten liefert:  . Dadurch wird aus der Exponentialgleichung eine einfache Umformung. Zum Beispiel wird aus
. Dadurch wird aus der Exponentialgleichung eine einfache Umformung. Zum Beispiel wird aus  sofort
sofort  .
.
-
Warum ist ln von 1 gleich 0?
 ist gleich 0, weil
ist gleich 0, weil  den Exponenten sucht, mit dem
den Exponenten sucht, mit dem  zu 1 wird. Da nach den Potenzgesetzen
zu 1 wird. Da nach den Potenzgesetzen  gilt, muss der gesuchte Exponent 0 sein. Deshalb gilt
gilt, muss der gesuchte Exponent 0 sein. Deshalb gilt  .
.
-
Wie wende ich die Produktregel beim ln richtig an?Die Produktregel beim natürlichen Logarithmus lautet:
 . Du ersetzt also den Logarithmus eines Produkts durch eine Summe aus zwei Logarithmen. Konkret bedeutet das: Statt
. Du ersetzt also den Logarithmus eines Produkts durch eine Summe aus zwei Logarithmen. Konkret bedeutet das: Statt  rechnest du
rechnest du  .
.
-
Wie wende ich die Potenzregel beim ln richtig an?Die Potenzregel beim natürlichen Logarithmus lautet:
 . Du darfst also den Exponenten vor den Logarithmus ziehen und mit
. Du darfst also den Exponenten vor den Logarithmus ziehen und mit  multiplizieren. Für Wurzeln gilt entsprechend:
multiplizieren. Für Wurzeln gilt entsprechend: ![Rendered by QuickLaTeX.com \ln\!\left(\sqrt[n]{x}\right)=\frac{1}{n}\ln(x)](https://blog.studyflix.de/wp-content/ql-cache/quicklatex.com-0b535ed3ea7b43c7f3fad8f0c6ff60aa_l3.png) .
.
Lösungen
In beiden Fällen bekommst du das Ergebnis mit dem natürlichen Logarithmus.
a) 
b) 

