ln Funktion
In diesem Artikel behandeln wir die ln Funktion. Dabei gehen wir auf den Zusammenhang zur Logarithmusfunktion und zur e Funktion ein. Zudem erklären wir dir die ln Regeln und rechnen Beispiele dazu.
Du bist eher der audiovisuelle Lerntyp? Dann sieh dir einfach unser Video dazu an.
Inhaltsübersicht
ln Funktion einfach erklärt
Die ln Funktion wird auch natürliche Logarithmusfunktion genannt. Denn sie entspricht der Logarithmusfunktion zur Basis e.
Die Funktionsvorschrift der ln Funktion lautet:

Dabei ist e eine Konstante, die sogenannte eulersche Zahl  .
.
ln Regeln
Für die Funktion ln(x) gelten bestimmte Rechenregeln, die sich aus denen der Logarithmusfunktionen ergeben.



Diese ln Gesetze erleichtern dir in vielen Fällen das Rechnen mit der Funktion ln x, wie die folgenden Beispiele zeigen:
Beispiel 1: 
Beispiel 2: 
Beispiel 3: 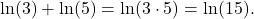
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Umkehrfunktion
Dementsprechend ist die Umkehrfunktion
von 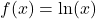 die e Funktion
die e Funktion

Für die ln Funktion und die e Funktion gilt daher:

Nullstelle
Da ln(x) eine Logarithmusfunktion ist, liefert dir ln(1) die Antwort auf die Frage: Mit welcher Zahl muss ich e potenzieren, damit ich eins erhalte? Es gilt  und somit
und somit

Damit hast du auch schon die einzige Nullstelle
der Funktion gefunden, nämlich 
Hinweis: Ebenfalls leicht zu berechnen ist ln(e). Hier stellst du dir wieder die Frage, mit welcher Zahl muss ich e potenzieren um e zu erhalten. Es gilt  und somit
und somit
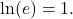
Monotonie
Eine weitere Eigenschaft, die du auch am Graph erkennen kannst, ist die strenge Monotonie der Funktion. Denn sie wächst stets weiter an.
Zudem verläuft der Graph nur im ersten und vierten Quadranten.
Das liegt daran, dass der Definitionsbereich von ln(x) nur den positiven reellen Zahlen entspricht, also

ln x ist demnach für negative x-Werte und  nicht definiert.
nicht definiert.
Der Grund hierfür ist, dass die e Funktion nur echt positive Werte annehmen kann und als Umkehrfunktion stimmt ihr Wertebereich mit dem Definitionsbereich von ln(x) überein.
Grenzverhalten
Hier untersuchst du das Grenzverhalten von ln(x) für  . Dafür siehst du dir an, wie sich die Funktion für x-Werte nahe der Null verhält. In diesem Fall nähert sie sich immer mehr der y-Achse und wird dabei immer negativer. Deshalb handelt sich bei der y-Achse um eine senkrechte Asymptote
und es gilt
. Dafür siehst du dir an, wie sich die Funktion für x-Werte nahe der Null verhält. In diesem Fall nähert sie sich immer mehr der y-Achse und wird dabei immer negativer. Deshalb handelt sich bei der y-Achse um eine senkrechte Asymptote
und es gilt

Für  lautet das Grenzverhalten der Funktion
lautet das Grenzverhalten der Funktion

Damit entspricht der Wertebereich von ln(x) den gesamten reellen Zahlen, das heißt

Ableitung und Stammfunktion
Weitere wichtige Eigenschaften der Funktion 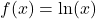 sind ihre
sind ihre
Zusammenfassung ln Funktion
Zum Schluss fassen wir alles noch einmal zusammen:
Die ln Funktion ist die natürliche Logarithmusfunktion mit der Eulerschen Zahl e als Basis. ln ist dabei die Abkürzung für den natürlichen Logarithmus. Mithilfe von Regeln und Gesetzen kannst du mit der ln Funktion rechnen und Ausdrücke mit ln vereinfachen.
| Funktion | 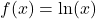 |
| Definitionsbereich |  |
| Wertebereich |  |
| Monotonie | streng monoton wachsend |
| Schnittpunkt mit der x-Achse |  |
| Schnittpunkt mit der y-Achse | gibt es nicht |
| Asymptote | senkrecht:  (y-Achse) (y-Achse) |
| Umkehrfunktion |
 (e Funktion
) (e Funktion
) |
| Ableitungsfunktion |  |
| Stammfunktion |  |


