Quadratische Funktionen
Quadratische Funktionen — was ist das? Hier erklären wir dir alles, was du wissen musst!
Inhaltsübersicht
Quadratische Funktionen einfach erklärt
Eine quadratische Funktion erkennst du daran, dass ein x2 vorkommt, aber kein x3, x4, x5, usw… Der Graph einer quadratischen Funktion ist eine Parabel.
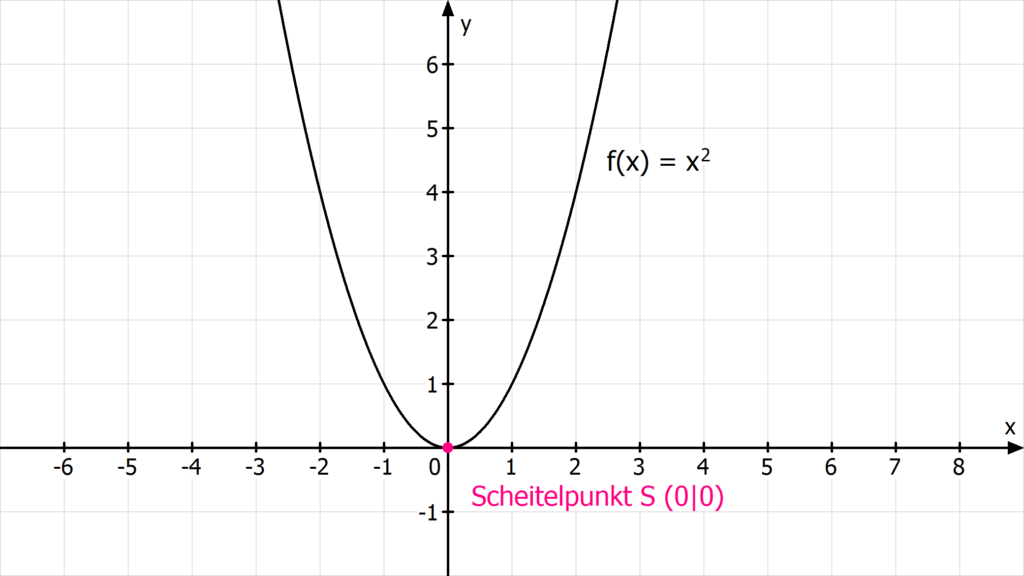
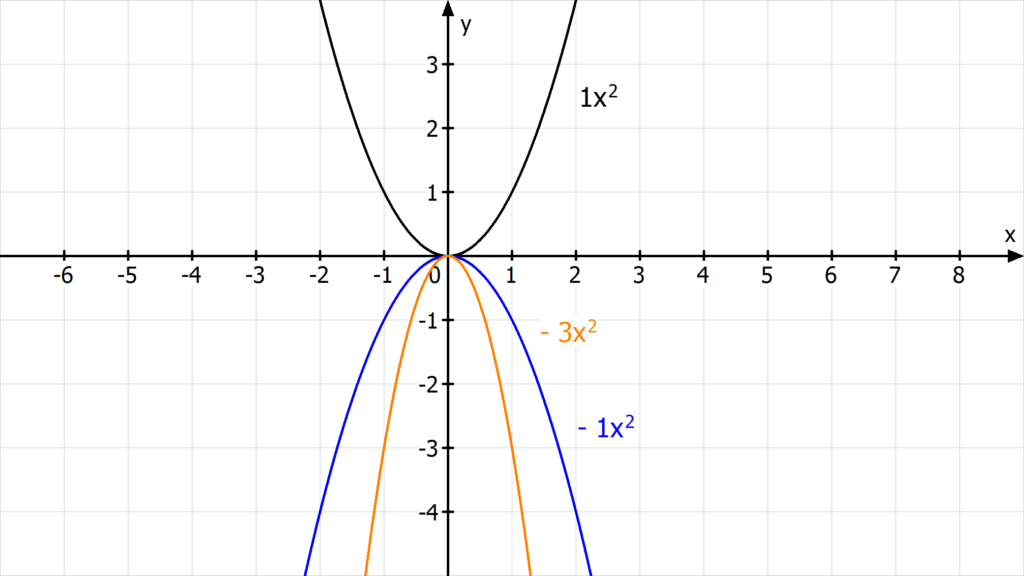
Hier siehst du den Graphen der einfachsten quadratischen Funktion f(x) = x2. Den nennst du Normalparabel.
Der Scheitelpunkt S ist der tiefste oder höchste Punkt einer Parabel. Bei einer Normalparabel liegt er im Punkt S(0|0).
Du kannst eine quadratische Funktion verändern, indem du
- den Scheitelpunkt S in y-Richtung verschiebst (oben oder unten).
- den Scheitelpunkt S in x-Richtung verschiebst (links oder rechts).
- die Parabel streckst (dünner machst) oder stauchst (breiter machst).
- sie an der x-Achse spiegelst (Öffnung zeigt nach unten).
Verschiebung in y-Richtung
Du kannst den Graphen einer quadratischen Funktion nach unten oder oben verschieben .
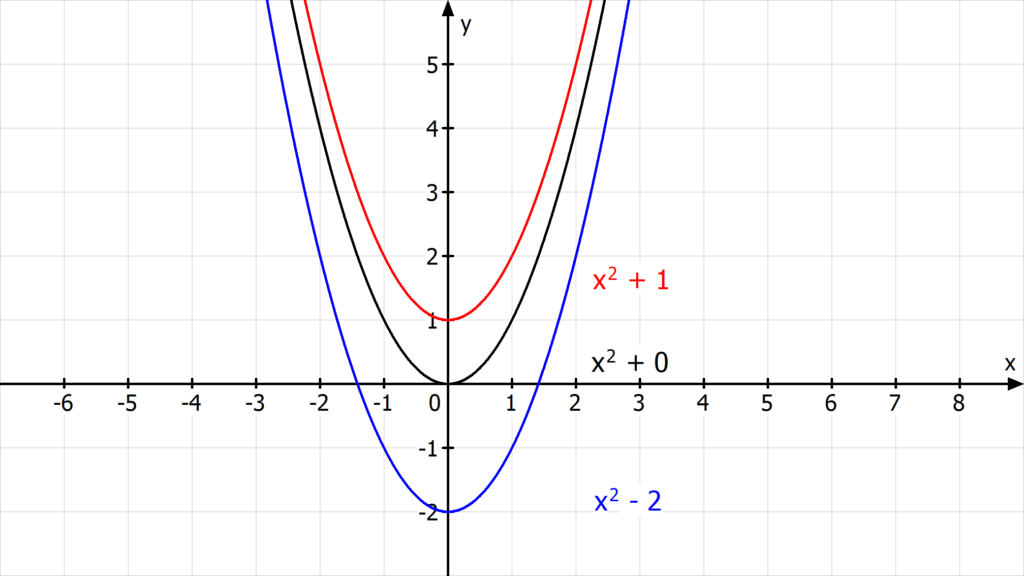
Hier wurde die Funktion um 1 Einheit nach oben verschoben. Hinter die Funktion f(x) = x2 schreibst du also + 1.
g(x) = x2+ 1
Verschiebst du die Normalparabel um 2 Einheiten nach unten, hängst du – 2 an die Funktion f(x) = x2 an.
h(x) = x2 – 2
Verschiebung um e nach oben: f(x) = x2 + e
Verschiebung um e nach unten: f(x) = x2 – e
Verschiebung in x-Richtung
Du kannst eine quadratische Funktion entlang der x-Achse nach rechts oder links verschieben.
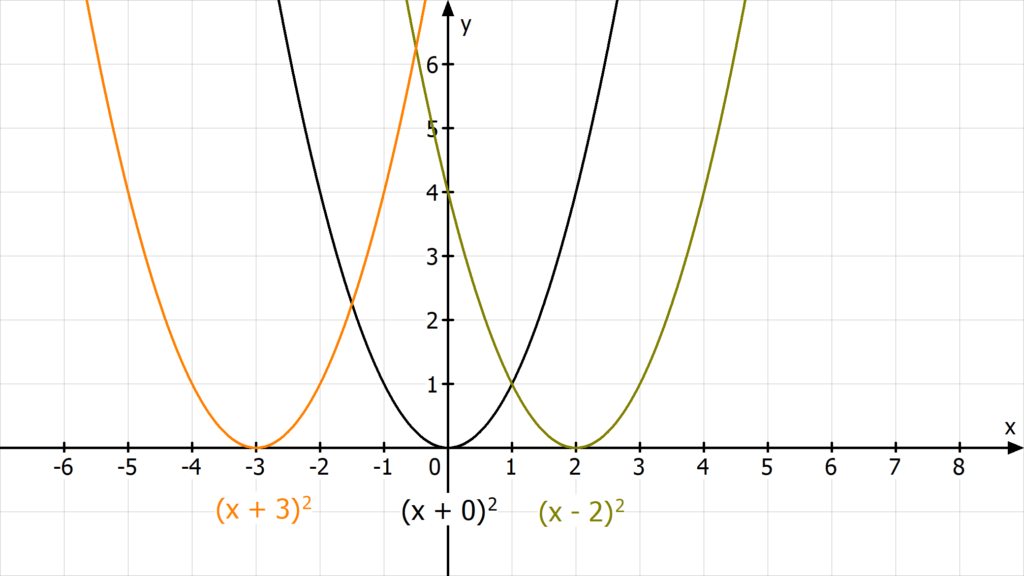
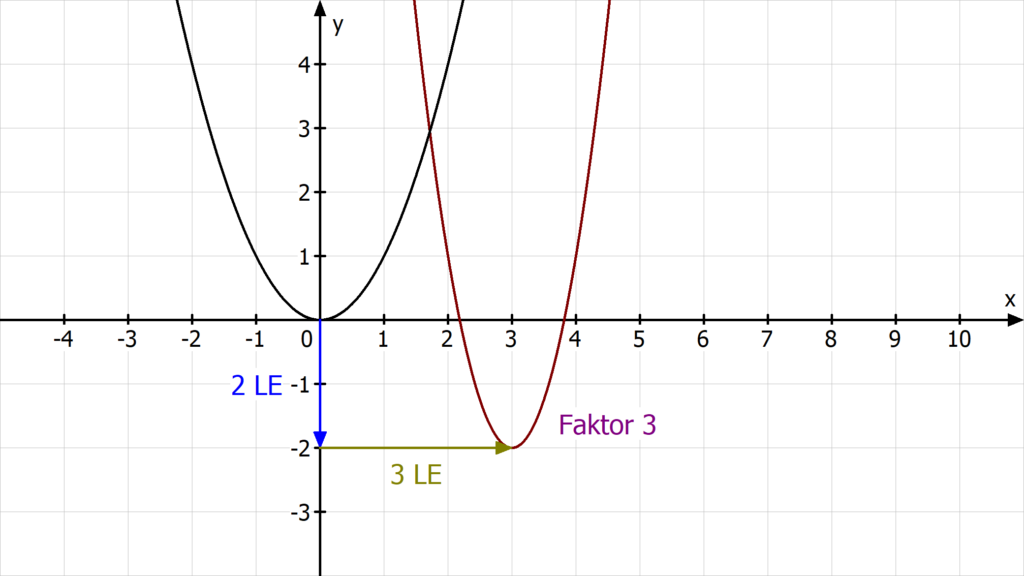
Willst du den Scheitelpunkt S einer Normalparabel f(x) = x2 um 2 Einheiten nach rechts verschieben, lautet die neue Funktionsgleichung
g(x) = (x – 2)2
Bei einer Verschiebung nach links um 3 Einheiten, schreibst du
h(x) = (x + 3)2
Eine Verschiebung in x-Richtung erkennst du an der Zahl innerhalb der Klammer. Steht vor der Zahl ein Minus (-), verschiebst du den Graphen nach rechts. Bei einem Plus (+) verschiebst du den Graphen der quadratischen Funktion nach links.
Verschiebung um d nach rechts: f(x) = (x – d)2
Verschiebung um d nach links: f(x) = (x + d)2
Streckung/Stauchung
Willst du eine quadratische Funktion strecken (schmaler) oder stauchen (breiter), rechnest du die Funktion mal den Wert a. Aus f(x) = x2 wird dann
f(x) = a · x2
Ist a größer als 1, wird der Graph schmaler. Er ist gestreckt.
Ist a größer als 0 und kleiner als 1, wird der Graph breiter. Er ist gestaucht.
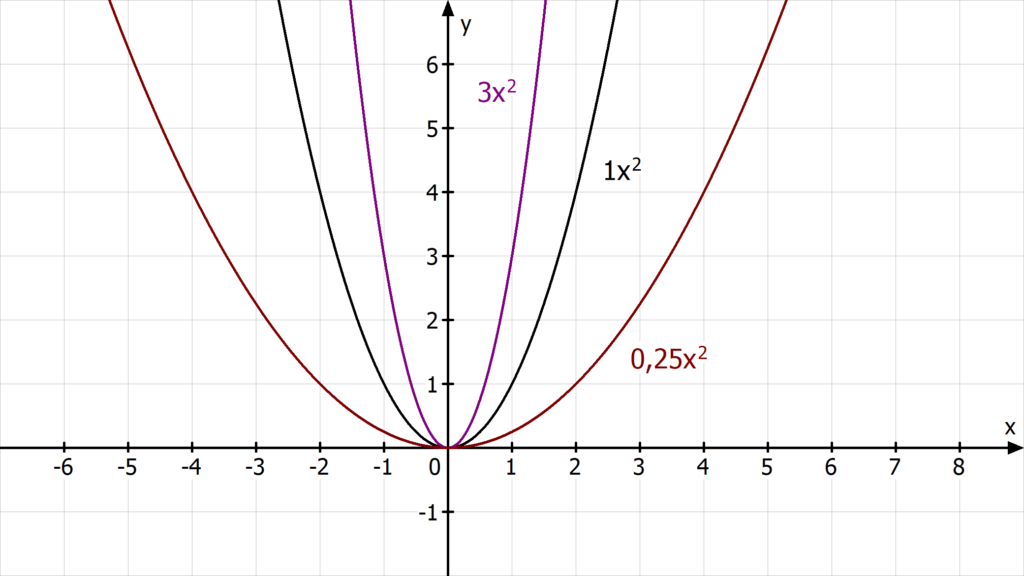
Die Funktion g(x) = 3 · x2 hat den Faktor 3. Die Parabel ist gestreckt, also schmaler als die Normalparabel.
Die Funktion h(x) = 0,25 · x2 hat den Faktor 0,25. Die Parabel ist gestaucht, also breiter als die Normalparabel.
Streckung (schmaler): f(x) = a · f(x) (a größer als 1; 1 < a)
Stauchung (breiter): f(x) = a · f(x) (a größer als 0 und kleiner als 1; 0 < a < 1)
Die Normalfunktion hat eigentlich den Faktor a = 1 (f(x) = 1 · x2). Du kannst ihn aber weglassen, weil sie weder gestreckt noch gestaucht wird.
Spiegelung an x-Achse
Wenn der Faktor a negativ ist, wird deine quadratische Funktion an der x-Achse nach unten gespiegelt.
Der blaue Graph ist eine gespiegelte Normalparabel. Sie hat die Funktionsgleichung
g(x) = – 1 · x2.
Die Funktion h(x) = – 3 · x2 hat den Faktor – 3. Du spiegelst die quadratische Funktion wegen dem Minus-Zeichen an der x-Achse und streckst sie wegen der Zahl 3.
Spiegelung, wenn Faktor a negativ.
h(x) = – 3 · x2 ist die Spiegelung von f(x) = 3 · x2.
Kombination
Bei quadratischen Funktionen kannst du natürlich auch gleichzeitig Verschiebungen, Stauchungen und Spiegelungen haben.
Schau dir die Funktion g(x) = 3 · (x – 3)2 -2 an.
Du erhältst den Graphen für g(x), indem du die Normalparabel f(x) = x2 entsprechend veränderst.
Um g(x) zu bekommen,
- verschiebst du f(x) um 2 Einheiten nach unten → f1(x) = x2 -2
- verschiebst du f1(x) um 3 Einheiten nach rechts → f2(x) = (x – 3)2 -2
- streckst du f2(x) mit dem Faktor 3 → f3(x) = 3 · (x – 3)2 -2
Bist du alle Veränderungen durchgegangen, erhältst du deine Funktion g(x) = 3 · (x – 3)2 -2.
Quadratische Funktionen Formel
Quadratische Funktionen kannst du auf verschiedene Weisen darstellen. Alle haben ihre Vor- und Nachteile.
- Scheitelpunktform: f(x) = a · (x – d)2 + e
- Allgemeine Form : f(x) = a · x2 + b · x +c
- Faktorisierte Form: f(x) = (x – x1) · (x – x2)
Die Scheitelpunktform zeigt dir direkt die Koordinaten des Scheitelpunkts S(d|e).
Die allgemeine Form kannst du direkt in die Mitternachtsformel einsetzen, um die Nullstellen auszurechnen.
Und bei der faktorisierten Form siehst du sofort die Nullstellen der quadratischen Funktion.
Du kannst eine Form auch in eine andere umwandeln. Willst du zum Beispiel die allgemeine Form in die Scheitelpunktform bringen, brauchst du die quadratische Ergänzung .
Funktionsgleichung bestimmen
Je nach deinen gegebenen Informationen, kannst du die Funktionsgleichungen von quadratischen Funktionen ganz einfach selbst bestimmen.
Hier zeigen wir dir das Vorgehen anhand eines Beispiels.
Beispiel: Funktionsgleichung von Parabeln bestimmen
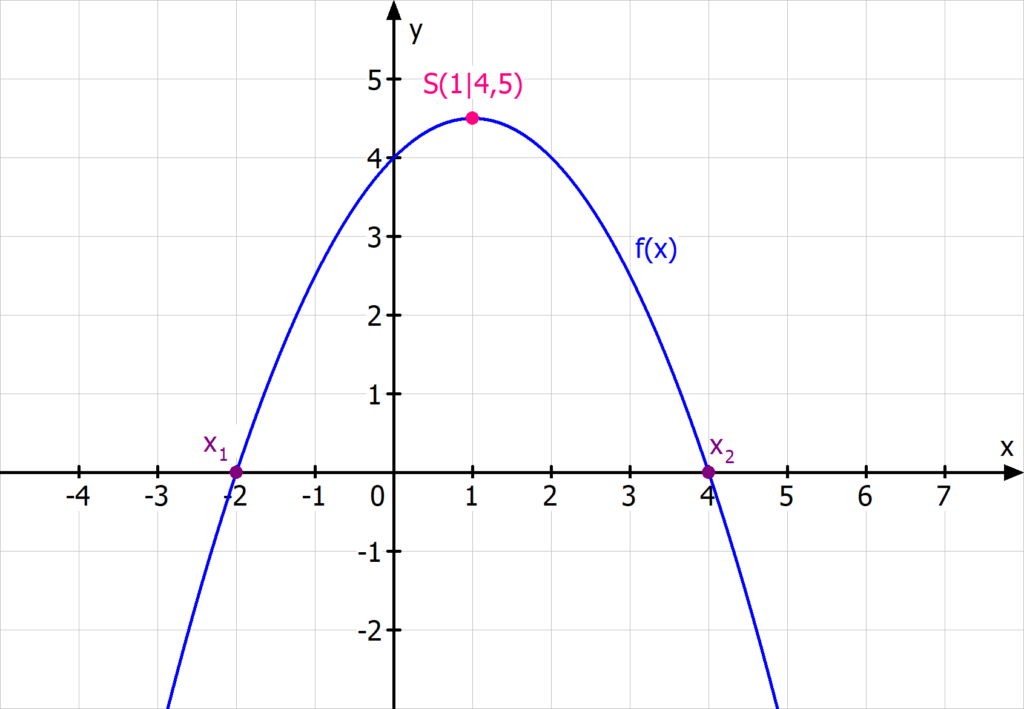
Stell dir vor, du hast eine Parabel mit dem Scheitelpunkt S(1|4,5), die außerdem durch den Punkt P(4|0) verläuft. Nun möchtest du die Funktionsgleichung berechnen.
Dann befolgst du am besten diese Schritt-für-Schritt-Anleitung:
- Schritt 1: Schreibe die Funktionsgleichung in Scheitelpunktform auf:
f(x) = a · (x – d)2 + e
- Schritt 2: Setze die Koordinaten des Scheitelpunktes S(1|4,5) mit e = 4,5 und d = 1 ein. Damit ergibt sich
f(x) = a · (x – 1)2 + 4,5
- Schritt 3: Um a zu berechnen, setzt du als nächstes den Punkt P(4|0) in die Funktionsgleichung ein:
0 = a · (4 – 1)2 + 4,5
0 = a · 32 + 4,5
0 = 9a + 4,5 | -4,5
| -4,5
– 4,5 = 9a | ÷ 9
| ÷ 9
a = – 0,5
- Schritt 4: Setze a in die Funktionsgleichung ein und multipliziere den Funktionsterm aus.
f(x) = – 0,5 (x – 1)2 + 4,5 = -0,5x2 + x + 4
Nullstellen berechnen
Quadratische Funktionen haben entweder eine, zwei oder gar keine Nullstelle.
Um die Nullstellen der quadratischen Funktion zu berechnen, kannst du verschiedene Tricks und Formeln benutzen. Den ausführlichen Artikel zum Berechnen von Nullstellen findest du hier .
Bei quadratischen Funktionen in faktorisierter Form f(x) = (x – x1) · (x – x2), kannst du die Nullstellen x1 und x2 direkt ablesen.
Bei der allgemeinen Form f(x) = a · x2 + b · x +c, kannst du die Mitternachtsformel verwenden.
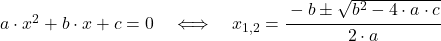
Hast du die Normalform mit a = 1 gegeben, kannst du auch die pq-Formel verwenden.
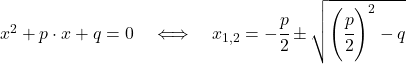
Für besonders schöne quadratische Funktionen kannst du auch den Satz von Vieta anwenden:
Hat 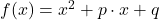 die beiden Nullstellen
die beiden Nullstellen 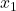 und
und 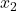 , so können sie wie folgt berechnet werden
, so können sie wie folgt berechnet werden
(I) 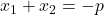 und (II)
und (II) 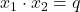
Eine quadratische Funktion in Scheitelpunktform kannst du nach x auflösen, indem du die Wurzel ziehst. Hier brauchst du weder Mitternachtsformel noch Vieta.
Ganzrationale Funktionen
Die quadratischen Funktionen hast du verstanden, aber du fragst dich, was es mit ganzrationalen Funktionen auf sich hat? Hier findest du alles, was du wissen musst!