Wann darf ich beim Koeffizientenvergleich einfach x wegkürzen?

Beim Koeffizientenvergleich darfst du ein gemeinsames wegkürzen, wenn die Gleichung als Polynomgleichheit für alle gelten soll und auf beiden Seiten derselbe Faktor in jedem Term vorkommt. Dann folgt aus für alle zwingend .

Wie bringe ich zwei Ausdrücke in die gleiche Polynomform?

Zwei Ausdrücke bringst du in die gleiche Polynomform, indem du zuerst alle Klammern ausmultiplizierst und Brüche auf einen gemeinsamen Nenner bringst, falls nötig. Danach fasst du gleichartige Terme zusammen und ordnest nach Potenzen: -Terme, dann -Terme, dann konstante Terme.

Was mache ich, wenn auf einer Seite ein x² fehlt?

Wenn auf einer Seite ein -Term fehlt, behandelst du den Koeffizienten vor dort als 0 und vergleichst trotzdem die Koeffizienten. Zum Beispiel wird aus in der Vergleichsform , damit du den -Koeffizienten sauber gleichsetzen kannst.

Welche Fehler passieren oft beim Zusammenfassen von Koeffizienten?

Häufige Fehler beim Zusammenfassen von Koeffizienten sind Vorzeichenfehler, das Vermischen verschiedener Potenzen und das Vergessen von . Beispiel: Aus wird fälschlich , richtig ist . Außerdem darfst du -Terme nie mit konstanten Termen addieren.

Wie prüfe ich schnell, ob meine gefundenen Werte stimmen?

Gefundene Werte prüfst du schnell, indem du sie in beide ursprünglichen Ausdrücke einsetzt und kontrollierst, ob für mehrere -Werte dieselben Ergebnisse herauskommen. Zum Beispiel testest du und : Stimmen beide Seiten jeweils überein, ist das ein starker Hinweis, dass die Koeffizienten korrekt sind.

Video

Quiz

Hier geht's zum Video „Partialbruchzerlegung“

Koeffizientenvergleich

Wichtige Inhalte in diesem Video

Koeffizientenvergleich einfach erklärt

(00:12)

Koeffizientenvergleich Beispiel

(01:07)

Hier erfährst du, was ein Koeffizientenvergleich ist und wie du ihn Schritt für Schritt durchführen kannst. In unserem Video erklären wir dir den Koeffizientenvergleich noch einmal an einem Beispiel. Schau es dir also unbedingt an!

Inhaltsübersicht

Koeffizientenvergleich einfach erklärt

im Videozur Stelle im Video springen

(00:12)

Mit einem Koeffizientenvergleich kannst du zwei Polynome untersuchen und dabei feststellen, ob die beiden Polynome gleich sind.

$P(x) = \textcolor{red}{a_0} + \textcolor{blue}{a_1}x^1+\textcolor{orange}{a_2}x^2+...+\textcolor{violet}{a_n}x^n$

$Q(x)=\textcolor{red}{b_0}+\textcolor{blue}{b_1}x^1+\textcolor{orange}{b_2}x^2+...+\textcolor{violet}{b_n}x^n$

Was ein ein Koeffizient?

Das sind die Ausdrücke vor den x-Potenzen.
Für : $\textcolor{red}{a_0},\textcolor{blue}{a_1}, \textcolor{orange}{a_2},...,\textcolor{violet}{a_n}$
Für : $\textcolor{red}{b_0},\textcolor{blue}{b_1}, \textcolor{orange}{b_2},...,\textcolor{violet}{b_n}$

Diese zwei Polynome P(x) und Q(x) haben den gleichen Grad, also x^n als höchste Potenz. Sie sind genau dann gleich, wenn alle ihre Koeffizienten, gleich sind.

P(x) = Q(x) , wenn

$\textcolor{red}{a_0}=\textcolor{red}{b_0} , \textcolor{blue}{a_1} = \textcolor{blue}{b_1}, ... , \textcolor{violet}{a_n}=\textcolor{violet}{b_n}$

Einen Koeffizientenvergleich kannst du aber auch gezielt nutzen, um zwei gegebene Polynome gleich zu machen. Die Polynome sind nämlich genau dann gleich, wenn alle einzelnen Teile, also gerade die Koeffizienten vor den entsprechenden x-Potenzen, gleich sind.

Koeffizientenvergleich Beispiel

im Videozur Stelle im Video springen

(01:07)

Schauen wir uns das gleich mal gemeinsam an einem Beispiel an. Die beiden Polynome P(x) und Q(x) sollen gleich sein.

P(x)=3x-1

Q(x)=a(x-1)+2b

Schritt 1: Ausmultiplizieren

Hier kommen noch Klammern in den Polynomen vor. Diese löst du zunächst einmal auf.

Q(x) = a(x-1)+2b

= ax-a+2b

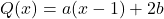
Schritt 2: Koeffizienten identifizieren

Beide Polynome haben Grad 1, weil das x die höchste Potenz ist, die in den Gleichungen vorkommt. Es gibt deshalb zwei Koeffizienten, die du vergleichen kannst.

Einmal gibt es die Koeffizienten vor dem x, hier sind sie rot markiert.

$P(x)=\textcolor{red}{3}x-1$

$Q(x)=\textcolor{red}{a}x+2b-a$

Außerdem gibt es noch die konstanten Glieder, also die Koeffizienten von x⁰=1. Das x^0 wird meistens nicht geschrieben, deshalb erkennst du diese Koeffizienten daran, dass kein x an ihnen hängt. Das ist in diesem Beispiel der ganze Rest, hier blau markiert.

$P(x)=3x+\textcolor{blue}{(-1)}$

$Q(x)=ax+\textcolor{blue}{2b-a}$

Wenn du die beiden Polynome gleichsetzt, findest du die entsprechenden Ausdrücke auf beiden Seiten der Gleichung wieder.

P(x) = Q(x)

$\textcolor{red}{3}x +\textcolor{blue}{(-1)}=\textcolor{red}{a}x+\textcolor{blue}{2b-a}$

Schritt 3: Gleichungssystem aufstellen

Jetzt kannst du die jeweiligen Koeffizienten gleichsetzen und so die Gleichungen aufstellen, mit denen du im nächsten Schritt weiterarbeitest.

$\textcolor{red}{3}x=\textcolor{red}{a}x$

$\textcolor{blue}{-1}=\textcolor{blue}{2b-a}$

Schritt 4: Gleichungen auflösen

Fast geschafft, nun musst du die Gleichungen nur noch auflösen. Durch das Wegkürzen von x in der ersten Gleichung ergibt sich schnell

3x=ax

a=3 .

Mit diesem Wissen kannst du nun auch die zweite Gleichung umformen und so b gewinnen.

-1=2b-3

3-1=2b

2=2b

b=1

Damit hast du die beiden Variablen a und b so bestimmt, dass die Polynome P(x) und Q(x) gleich sind.

P(x)=3x-1

Q(x)=a(x-1)+2b

=3x-3+2=3x-1

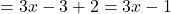
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich

Koeffizientenvergleich — häufigste Fragen

(ausklappen)

Wann darf ich beim Koeffizientenvergleich einfach x wegkürzen?

Beim Koeffizientenvergleich darfst du ein gemeinsames wegkürzen, wenn die Gleichung als Polynomgleichheit für alle gelten soll und auf beiden Seiten derselbe Faktor in jedem Term vorkommt. Dann folgt aus für alle zwingend .
Wie bringe ich zwei Ausdrücke in die gleiche Polynomform?

Zwei Ausdrücke bringst du in die gleiche Polynomform, indem du zuerst alle Klammern ausmultiplizierst und Brüche auf einen gemeinsamen Nenner bringst, falls nötig. Danach fasst du gleichartige Terme zusammen und ordnest nach Potenzen: -Terme, dann -Terme, dann konstante Terme.
Was mache ich, wenn auf einer Seite ein x² fehlt?

Wenn auf einer Seite ein -Term fehlt, behandelst du den Koeffizienten vor dort als 0 und vergleichst trotzdem die Koeffizienten. Zum Beispiel wird aus in der Vergleichsform $0\cdot x^2+2x+5$ , damit du den -Koeffizienten sauber gleichsetzen kannst.
Welche Fehler passieren oft beim Zusammenfassen von Koeffizienten?

Häufige Fehler beim Zusammenfassen von Koeffizienten sind Vorzeichenfehler, das Vermischen verschiedener Potenzen und das Vergessen von . Beispiel: Aus wird fälschlich , richtig ist . Außerdem darfst du -Terme nie mit konstanten Termen addieren.
Wie prüfe ich schnell, ob meine gefundenen Werte stimmen?

Gefundene Werte prüfst du schnell, indem du sie in beide ursprünglichen Ausdrücke einsetzt und kontrollierst, ob für mehrere -Werte dieselben Ergebnisse herauskommen. Zum Beispiel testest du und : Stimmen beide Seiten jeweils überein, ist das ein starker Hinweis, dass die Koeffizienten korrekt sind.

Koeffizientenvergleich Partialbruchzerlegung

im Videozum Video springen

So einen Koeffizientenvergleich musst du meistens im Zuge einer Partialbruchzerlegung durchführen. Dabei möchtest du eine rationale Funktion als Summe verschiedener Brüche darstellen. Betrachte folgendes Beispiel.

$3x^2+4x+2 \overset{!}{=} a_{11}(x^2+1)+(a_{21}x+b_{21})(x-1)$

Du folgst einfach Schritt für Schritt der Anleitung für den Koeffizientenvergleich.

Schritt 1: Ausmultiplizieren

Zuerst musst du die rechte Seite der Gleichung von allen Klammern befreien.

$3x^2+4x+2=a_{11}x^2+a_{11}+a_{21}x^2-a_{21}x+b_{21}x-b_{21}$

Damit kannst du nun weiterarbeiten.

Schritt 2: Koeffizienten identifizieren

Jetzt fasst du die Koeffizienten auf der rechten Seite zusammen. Dabei unterscheidest du zwischen Faktoren vor x^2 , vor und den konstanten Gliedern ohne ein x. Wir haben sie dir hier einmal in unterschiedlichen Farben markiert.

$\textcolor{red}{3}x^2+\textcolor{blue}{4}x+\textcolor{orange}{2}=\textcolor{red}{a_{11}}x^2\textcolor{orange}{+a_{11}}+\textcolor{red}{a_{21}}x^2+\textcolor{blue}{(-a_{21})}x+\textcolor{blue}{b_{21}}x+\textcolor{orange}{(-b_{21})}$

$\textcolor{red}{3}x^2+\textcolor{blue}{4}x+\textcolor{orange}{2}=\textcolor{red}{(a_{11}+a_{21})}x^2+\textcolor{blue}{(-a_{21}+b_{21})}x+\textcolor{orange}{a_{11}-b_{21}}$

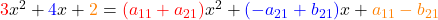
Schritt 3: Gleichungssystem aufstellen

Du siehst schon an den drei verschiedenen Farben, dass du hier drei Gleichungen aufstellen kannst.

$\textcolor{red}{3}=\textcolor{red}{a_{11}+a_{21}}$

$\textcolor{blue}{4}=\textcolor{blue}{b_{21}-a_{21}}$

$\textcolor{orange}{2}=\textcolor{orange}{a_{11}-b_{21}}$

Schritt 4: Gleichungssystem lösen

Jetzt musst du das Gleichungssystem lösen.

$\left(\begin{array}{rrr}1&1&0\\0&-1&1\\1&0&-1\\\end{array}\left|\begin{array}{r}3&4&2\\\end{array}\right)$

Als nächstes formst du die Matrix um, sodass du links von der Trennlinie die Einheitsmatrix erhältst. Das funktioniert beispielsweise mit dem Gauß-Algorithmus in mehreren Schritten.

$\left(\begin{array}{rrr}1&0&0\\0&1&0\\0&0&1\\\end{array}\left|\begin{array}{r}4,5&-1,5&2,5\\\end{array}\right)$

Nun kannst du den Wert der einzelnen Variablen einfach ablesen.

$a_{11}=4,5$ , $a_{21} = -1,5$ , $b_{21}=2,5$

Der Koeffizientenvergleich ist aber an dieser Stelle schon abgeschlossen, denn mit diesen Werten für die Variablen sind die beiden Polynome gleich.

$3x²+4x+2\overset{!}{=}a_{11}(x^2+1)+(a_{21}x+b_{21})(x-1)$