Funktionstypen
Du möchtest wissen, welche Funktionstypen es alles gibt und welche Eigenschaften sie haben? Das alles erfährst du hier in unserem Beitrag und im Video !
Inhaltsübersicht
Welche Funktionstypen gibt es?
Es gibt eine Menge unterschiedlicher Funktionstypen, alle mit verschiedenen Eigenschaften. Das hier sind die wichtigsten Funktionen auf einen Blick:
- Lineare Funktionen
z. B. f(x) = 2x + 3 - Quadratische Funktionen
z. B. f(x) = x² + 4x + 5 - Potenzfunktionen
z. B. f(x) = 9x5 - Wurzelfunktionen
z. B. f(x) =
- Ganzrationale Funktionen
z. B. f(x) = 3x4 + 7x³ + 2x² + x + 8 - Gebrochen-rationale Funktionen
z. B. f(x) =
- Exponentialfunktionen
z. B. f(x) = 4e2x - Logarithmusfunktionen
z. B. f(x) = ln(2x + 5) - Trigonometrische Funktionen
z. B. f(x) = sin(x)
Was jede Funktion ausmacht, wie sie aussehen und was ihre wichtigsten Eigenschaften sind, erfährst du jetzt!
Lineare Funktion
Lineare Funktionen haben eine Steigung m, die sich niemals ändert. Oft werden sie einfach Geraden genannt. Ein Beispiel wäre f(x) = 3x + 2.
f(x) = m ⋅ x + t
- m = Steigung der Geraden
- t = Schnittpunkt mit der y-Achse (y-Achsenabschnitt)
Tipp: Die Darstellung „f(x) =“ bedeutet das Gleiche wie „y = “. Es handelt sich nur um eine andere Schreibweise.
Die Steigung m kannst du mit dem Steigungsdreieck und folgender Formel berechnen:
m = 
Für (x1 | y1) und (x2 | y2) nimmst einfach du zwei beliebige Punkte, die auf der Geraden liegen.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Quadratische Funktion
Quadratische Funktionen bezeichnest du auch als Parabeln. Sie haben einen bogenförmigen Verlauf. Eine Parabel könnte z. B. diese Form haben: f(x) = 3x² + 6x + 2.
f(x) = ax2 + bx + c
Besonders wichtig ist bei einer quadratischen Funktion der Vorfaktor a. Er sagt dir einiges über die Eigenschaften der Parabel.
- | a | > 1 (Betrag von a größer als 1) → Parabel gestreckt
- | a | < 1 (Betrag von a kleiner als 1) → Parabel gestaucht
- | a | = 1 (Betrag von a gleich 1) → Normalparabel (keine Stauchung / Streckung)
- a > 0 (a ist positiv) → Parabel nach oben geöffnet
- a < 0 (a ist negativ) → Parabel nach unten geöffnet
Es gibt auch noch zwei alternative Darstellungsweisen:
-
Scheitelpunktform:
a(x – xS)2 + yS
Wie der Name schon sagt, gibt die Scheitelpunktform den Scheitelpunkt (xS | yS) an. Der ist jeweils der höchste oder niedrigste Punkt einer Parabel.
-
Faktorisierte Form:
a(x – x1)(x – x2)
Die faktorisierte Form hat den großen Vorteil, dass du direkt die Nullstellen der Parabel ablesen kannst. Du musst dafür deinen x-Wert immer so wählen, dass in den Klammern „0“ herauskommt.
Potenzfunktionen
Bei Potenzfunktionen kannst du zwischen verschiedenen Arten unterscheiden. Das liegt daran, dass der jeweilige Exponent großen Einfluss auf die Form hat. Eine Funktion könnte folgendermaßen aussehen: f(x) = 2x4
f(x) = a ⋅ xn
a = Vorfaktor
n = Exponent
Positiver Exponent n
Der Exponent n und der Vorfaktor a geben an, wie deine Funktion aussieht und verläuft. Schauen wir uns zunächst an, wie der Vorfaktor a den Verlauf beeinflusst, wenn n positiv ist.
Funktion mit geradem, positiven Exponenten:
- a > 0 (a ist positiv) → Funktion verläuft vom 2. in den 1. Quadranten
- a < 0 (a ist negativ) → Funktion verläuft vom 3. in den 4. Quadranten
Funktion mit ungeradem, positiven Exponenten:
- a > 0 (a ist positiv) → Funktion verläuft vom 3. in den 1. Quadranten
- a < 0 (a ist negativ) → Funktion verläuft vom 2. in den 4. Quadranten
Negativer Exponent n
Es ist ebenfalls möglich, dass n einen negativen Wert annimmt. Wenn dein Exponent negativ wird, kannst du diesen auch als Bruch darstellen:
x-n = 
Das n und a zeigen dir an, wie die Funktion verläuft.
Funktion mit geradem, negativen Exponenten:
- a > 0 (a ist positiv) → Funktion verläuft vom 2. in den 1. Quadranten
- a < 0 (a ist negativ) → Funktion verläuft vom 3. in den 4. Quadranten
Funktion mit ungeradem, positiven Exponenten:
- a > 0 (a ist positiv) → Funktion verläuft vom 3. in den 1. Quadranten
- a < 0 (a ist negativ) → Funktion verläuft vom 2. in den 4. Quadranten
Solche Funktionen nennst du auch gebrochen-rationale Funktionen. Die „Sprünge“, die die Funktion macht, heißen Definitionslücken.
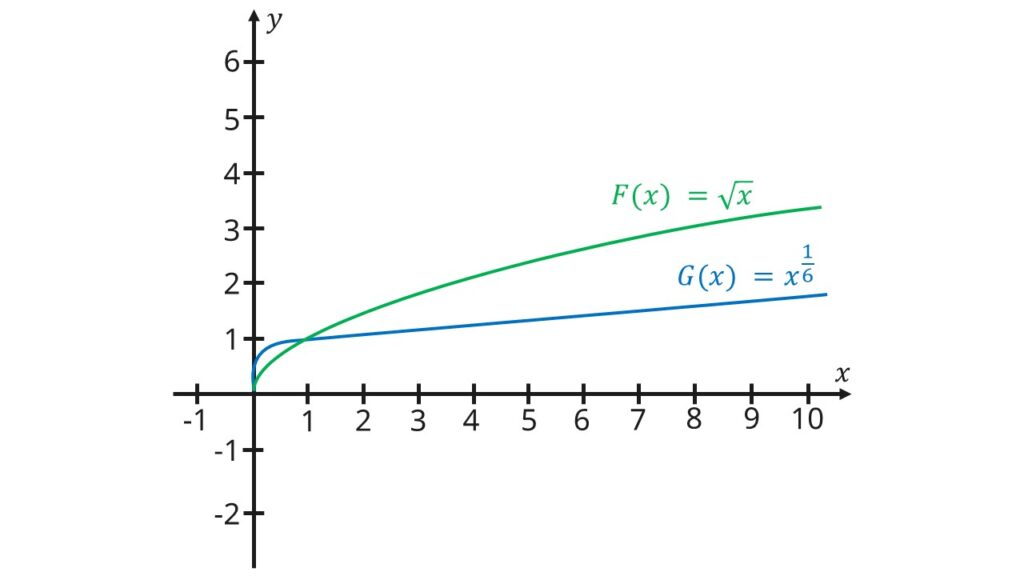
Wurzelfunktionen
Die Wurzelfunktion
ist die Umkehrfunktion
zur Potenzfunktion. Sie könnte beispielsweise so aussehen: 
f(x) = ![Rendered by QuickLaTeX.com \sqrt[n]{x}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-37ee09de0605d60b2a18b131332d5731_l3.png)
Das n ist dabei der sogenannte Wurzelexponent. Da die Wurzel quasi das Gegenstück zur Potenz ist, kannst du die Wurzelfunktion auch auf andere Weise darstellen.
![Rendered by QuickLaTeX.com \sqrt[n]{x}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-37ee09de0605d60b2a18b131332d5731_l3.png) =
= 
Die häufigste Wurzelfunktion, mit der du arbeitest, ist die Quadratwurzelfunktion. Bei dieser ist dein n gleich 2. Sie wird so häufig verwendet, dass du die 2 eigentlich gar nicht mehr hinschreiben musst. Das sieht dann so aus:
f(x) = 
Wichtig: Du darfst nicht vergessen, dass du für eine Quadratwurzelfunktion nur x ≥ 0 einsetzen darfst. Negative Zahlen funktionieren nicht.
Ganzrationale Funktionen
Ganzrationale Funktionen bestehen aus mehreren Termen der Form a ⋅ xn. Beispielsweise wäre f(x) = 4x³ + 5x² – 3x – 1 eine ganzrationale Funktion.
f(x) = an ⋅ xn + an-1 ⋅ xn-1 + … + a2 ⋅ x2 + a1 ⋅ x1 + a0
an bis a0 sind dabei immer die unterschiedlichen Vorfaktoren vor den jeweiligen xn bis x0. Und wie schon bei den Potenzfunktionen gibt der Exponent n und der dazugehörige Vorfaktor an den Gesamtverlauf der Funktion an.
Um ganzrationale Funktionen zu unterscheiden, verwendest du den sogenannten Grad n der Funktion. Das ist der höchste Exponent, denn du in der Funktion findest. Beispielsweise wäre f(x) = 4x³ + 5x² – 3x – 1 eine ganzrationale Funktion 3. Grades, weil ihr höchster Exponent 3 ist.
Schon gewusst: Eine andere Bezeichnung für ganzrationale Funktion ist Polynomfunktion. Ein Polynom besteht nämlich aus einer Vielzahl an Termen der Form an ⋅ xn.
Gebrochen rationale Funktionen
Gebrochen rationale Funktionen
zeichnen sich dadurch aus, dass sie als Bruch dargestellt werden. Dieser Bruch hat sowohl im Zähler
als auch im Nenner ein Polynom. Ein Beispiel dafür wäre folgende Funktion: f(x) = 
f(x) =  =
= 
Gebrochen-rationale Funktionen können Definitionslücken bzw. Polstellen aufweisen. Das bedeutet, dass das Polynom im Nenner der Funktion gleich 0 wird. Da du aber nie durch 0 teilen darfst, musst du diese Zahl aus der Definitionsmenge ausschließen. Solche Stellen siehst du auch in der Funktion und nennst du senkrechte Asymptoten.
Es gibt aber auch noch waagrechte und schräge Asymptoten. Diese werden durch den größten Exponenten im Zähler und Nenner der Funktion bestimmt:
- Exponent im Zähler ≤ Exponent im Nenner: waagrechte Asymptote
- Exponent im Zähler > Exponent im Nenner: schräge Asymptote
Exponentialfunktionen
Eine Exponentialfunktion ist eine Funktion, die ein exponentielles Wachstum darstellt. Die bekannteste Exponentialfunktion ist die e Funktion. Eine Exponentialfunktion könnte so f(x) = 0,25 ⋅ 2x oder so f(x) = 3e2x aussehen.
Exponentialfunktion: f(x) = a ⋅ bx
- a = Anfangswert
b = Basis
e Funktion: f(x) = ex
- e = Basis (Eulersche Zahl: 2,718…)
Die Basis b gibt dabei das Wachstum der Funktion an.
- b > 1 → Funktion steigt streng monoton
- 0 < b < 1 → Funktion fällt streng monoton
Besonders interessant ist, dass die normale Exponentialfunktion keine Nullstellen aufweist. Stattdessen nähert sie sich der x-Achse unendlich nah an.
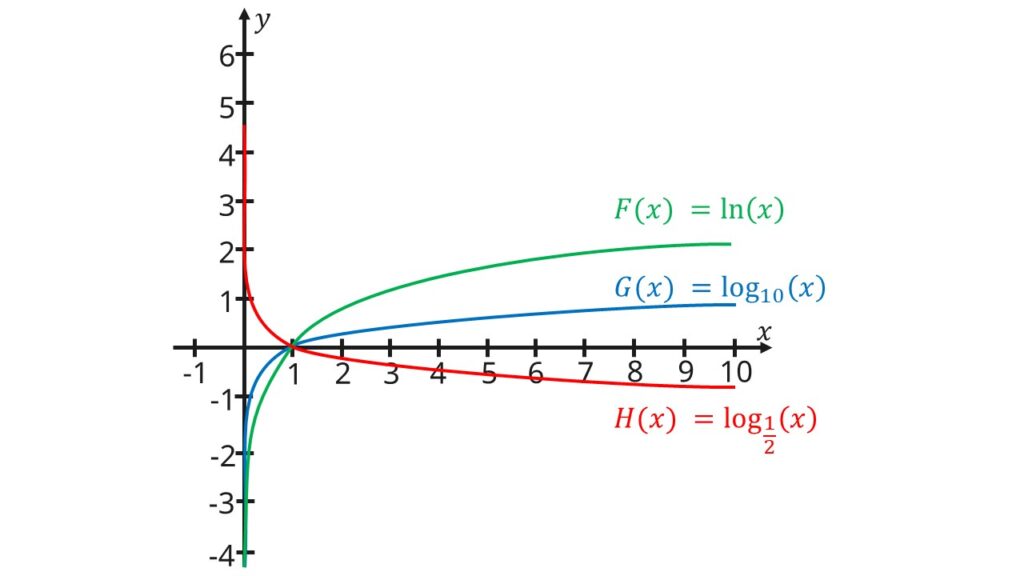
Logarithmusfunktionen
Das Gegenstück zur Exponentialfunktion ist die Logarithmusfunktion. Mit ihrer Hilfe kannst du Exponentialfunktionen nach x auflösen. Ein Beispiel dafür wäre diese Funktion: f(x) = ln(2x²)
f(x) = logb(x)
f(x) = ln(x)
- b = Basis
Die ln Funktion ist die gängigste Logarithmusfunktion. Sie wird auch natürlicher Logarithmus genannt und hat e als Basis. Ansonsten gibt es noch log(x), auch Zehnerlogarithmus genannt, da seine Basis b gleich 10 ist.
Beim Logarithmus musst du darauf aufpassen, dass dein x immer größer 0 ist. Das liegt daran, da der Logarithmus weder im Negativen noch bei 0 definiert ist.
Trigonometrische Funktionen
Die drei wichtigsten und bekanntesten trigonometrischen Funktionen sind die Sinus-, Cosinus- und Tangens-Funktion.
f(x) = sin(x)
f(x) = cos(x)
f(x) = tan(x)
Alle diese Funktionen zeichnen sich durch ihre Periodizität aus. Das bedeutet, dass sich ihr Verlauf in regelmäßigen Abständen wiederholt.
Durch die Periodizität kannst du auch immer einige Eigenschaften der Funktionen sicher vorhersagen. Der Faktor k stellt dabei dar, in der wievielten Periode der Funktion du dich gerade befindest.
- Definitionsbereich: Alle reellen Zahlen R
- Wertebereich: [-1, 1]
- Nullstellen: xk = k ⋅ π
- Hochpunkte: xk =
 + 2 ⋅ k ⋅ π
+ 2 ⋅ k ⋅ π - Tiefpunkte: xk =
 + 2 ⋅ k ⋅ π
+ 2 ⋅ k ⋅ π
- Definitionsbereich: Alle reellen Zahlen R
- Wertebereich: [-1, 1]
- Nullstellen: xk =
 + k ⋅ π
+ k ⋅ π - Hochpunkte: xk = 2 ⋅ k ⋅ π
- Tiefpunkte: xk = π + 2 ⋅ k ⋅ π
- Definitionsbereich: R \

- Wertebereich: Alle reellen Zahlen R
- Nullstellen: xk = k ⋅ π
- Senkrechte Asymptoten: xk =

Schon gewusst: Die trigonometrischen Funktionen werden auch Winkelfunktionen genannt. Das liegt daran, dass du mit ihnen die Winkel und Seitenlängen eines rechtwinkligen Dreiecks beschreiben kannst.
Funktionstypen — häufigste Fragen
(ausklappen)
Funktionstypen — häufigste Fragen
(ausklappen)-
Wie erkenne ich den Funktionstyp nur am Graphen?Den Funktionstyp erkennst du am Graphen an typischen Formen und Asymptoten: Eine lineare Funktion ist eine Gerade, eine quadratische Funktion ist eine Parabel, Exponentialfunktionen nähern sich oft einer waagrechten Linie an und gebrochen-rationale Funktionen zeigen häufig „Lücken“ mit senkrechten Asymptoten.
-
Welche Fehler passieren oft beim Definitionsbereich von Wurzel und Logarithmus?Häufige Fehler beim Definitionsbereich sind: Bei Wurzeln wird vergessen, dass bei gerader Wurzel der Radikand
 sein muss und bei Logarithmen, dass das Argument strikt
sein muss und bei Logarithmen, dass das Argument strikt  sein muss. Beispiel:
sein muss. Beispiel:  ist erst für
ist erst für  definiert, nicht für
definiert, nicht für  .
.
-
Wie unterscheide ich eine Potenzfunktion mit negativem Exponenten von einer gebrochen-rationalen Funktion?Eine Potenzfunktion mit negativem Exponenten hat die Form
 und ist damit ein Spezialfall einer gebrochen-rationalen Funktion. Gebrochen-rationale Funktionen sind allgemeiner und haben
und ist damit ein Spezialfall einer gebrochen-rationalen Funktion. Gebrochen-rationale Funktionen sind allgemeiner und haben  mit Polynomen im Zähler und Nenner, nicht nur eine einzelne Potenz.
mit Polynomen im Zähler und Nenner, nicht nur eine einzelne Potenz.
-
Wann hat eine gebrochen-rationale Funktion eine waagrechte Asymptote?Eine gebrochen-rationale Funktion hat eine waagrechte Asymptote, wenn der Grad (höchster Exponent) im Zähler kleiner oder gleich dem Grad im Nenner ist. Dann nähert sich der Graph für große
 einem konstanten Wert an. Bei kleinerem Zählergrad ist die Asymptote oft
einem konstanten Wert an. Bei kleinerem Zählergrad ist die Asymptote oft  .
.
-
Wie finde ich bei Sinus und Cosinus die Periode?Die Periode von Sinus und Cosinus findest du über den Faktor vor
 : Bei
: Bei  oder
oder  gilt
gilt  . Beispiel: Für
. Beispiel: Für  ist die Periode
ist die Periode  , weil die Schwingung dreimal schneller abläuft.
, weil die Schwingung dreimal schneller abläuft.
Nullstellen berechnen
Jetzt weißt du mehr über die verschiedenen Arten von Funktionen und deren Eigenschaften. Um noch mehr über eine Funktion herauszufinden, musst du jetzt noch wissen, wie du deren Nullstellen berechnest. Wie du die Nullstellen berechnest, erklären wir dir hier.