Quadratische Ergänzung
Mit der quadratischen Ergänzung kannst du quadratische Funktionen in ihre Scheitelpunktform und quadratische Gleichungen in Binomische Formeln umwandeln. Schau dir unser passendes Video dazu an!
Inhaltsübersicht
Quadratische Ergänzung einfach erklärt
Die quadratische Ergänzung ist eine Technik, um eine quadratische Gleichung von ihrer Normalenform in Scheitelpunktform umzuwandeln. Das macht das Nullstellen berechnen einer quadratischen Funktion einfacher. Außerdem kannst du auf einen Blick den Scheitelpunkt bestimmen S(d|e).
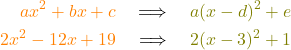
Der Trick ist, deine quadratische Gleichung f(x) = x2 + 2bx + c mit der Zahl +b2-b2 zu addieren. Dadurch hast du in deiner quadratischen Gleichung die binomische Formel x2 + 2bx + b2 stehen. Die binomische Formel kannst du durch (x+b)2 ersetzen und bekommst die Scheitelpunktform f(x) = (x+b)2 -b2 + c.
![Rendered by QuickLaTeX.com \[ f(x) = x^2 + 2bx + c \;\Longrightarrow\; f(x) = x^2 + 2bx \underbrace{ \textcolor{red}{+ b^2} \textcolor{blue}{ - b^2 } }_{=0} + c \;\Longrightarrow\; f(x) = (x+b)^2 \textcolor{blue}{ - b^2 } + c \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-eba1ee7a2d72c3f18260171e6a86dc2c_l3.png)
Wie funktioniert quadratisch ergänzen?
Wozu die quadratische Ergänzung nützt, hast du gerade eben gesehen. Mit ihrer Hilfe kannst du verschiedene quadratische Terme auf die Form einer binomischen Formel bringen. Schaue dir zum Beispiel die Parabelgleichung f(x)=2x2-8x an. Um sie in eine binomische Formel zu verwandeln, musst du dich nur an folgende Schritt-für-Schritt-Anleitung für die quadratische Ergänzung halten:
- Schritt 1: Klammere die Zahl (Faktor) vor dem quadratischen Term x2 aus
![Rendered by QuickLaTeX.com \[f(x)=2x^2-8x= 2(x^2-4x).\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-4ee31bb2901b4805f6436b5eebb1ce89_l3.png)
- Schritt 2: Entscheide, welche der drei binomischen Formeln du brauchst. Du willst den Ausdruck in der Klammer x2-4x als eine binomische Formel schreiben. Weil du einen Term mit x2 und einen zweiten Term nur mit x hast, brauchst du entweder die erste oder zweite binomische Formel. Das negative Vorzeichen bei -4x verrät dir, dass du die zweite binomische Formel benutzen musst:
![Rendered by QuickLaTeX.com \[a^2\textcolor{red}{-2ab} + b^2 = (a-b)^2.\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-dcbf27828f4d130604c7942b2a5de3f6_l3.png)
- Schritt 3: Finde heraus, welchen Wert deine Variablen a und b in der binomischen Formel a2 -2ab + b2 haben. Weil in x2-4x ein x2 auftaucht, muss a=x sein. Weil 4x kein x2 enthält, muss 4x=2ab sein. Du kannst a=x einsetzen und bekommst b=2:
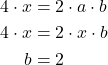
- Schritt 4: Jetzt hast du ein Problem. In deiner quadratischen Gleichung x2-4x fehlt dir ein Term, um es als binomische Formel zu schreiben. Du hast x2=a2 und -4x=-2ab. Es fehlt b2. Das löst du mit der quadratischen Ergänzung. Dafür addierst du +b2=+4 (b2=22=4) zu deiner Gleichung. Damit sich deine Gleichung nicht ändert, musst du gleichzeitig -b2=-4 rechnen (Äquivalenzumformung ):
![Rendered by QuickLaTeX.com \[ f(x)=2(x^2-4x \underbrace{ \textcolor{blue}{+4}\textcolor{red}{-4} }_{=0} ) = 2 [ (x-2)^2\textcolor{red}{-4} ]\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-fbd62f12f0c8af5c7caf5b9e6a5f275e_l3.png)
Weil du dieselbe Zahl addierst und sofort wieder abziehst, rechnest du eigentlich nur plus 0. Dadurch veränderst du die Lösung deiner Gleichung nicht! Es ist also eine Äquivalenzumformung .
- Schritt 5: Jetzt brauchst du nur noch ausmultiplizieren und du hast die Scheitelpunktform gefunden:
![Rendered by QuickLaTeX.com \[ f(x) = 2 [ (x-2)^2-4 ] = 2(x-2)^2 -8 \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-f744189855419ff97e470c8efff03127_l3.png)
Quadratisch ergänzen ist gar nicht so schwer, oder?
Sonderfall bx=0
Du solltest die quadratische Ergänzung aber nicht blind anwenden. Es gibt auch Fälle, in denen du es dir noch leichter machen kannst. Wenn bei deiner quadratischen Gleichung ax2 + bx + c der lineare Term bx fehlt (bx=0), kannst du dir beim quadratischen Ergänzen viel Arbeit sparen. Weil b=0 ist, müsste die quadratische Ergänzung +0^2-0^2 sein. Das ändert aber nichts an deiner ursprünglichen Gleichung.
![Rendered by QuickLaTeX.com \[ ax^2 \textcolor{red}{+0^2}\textcolor{blue}{-0^2} +c = a^x + c \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-a22a6e9a78b24adb86d8d9e29b4e633d_l3.png)
Die Normalform ist in diesem Sonderfall also schon die Scheitelpunktform. Den Scheitelpunkt berechnen ist dann ganz einfach: Er liegt bei S(0|c).
Wozu brauchst du quadratische Ergänzungen?
Du hast gesehen, dass du mit dieser Methode bei Parabelgleichung den Scheitelpunkt bestimmen kannst, indem du die quadratische Funktion von ihrer Normalform in Scheitelform umrechnest. Quadratisch ergänzen hilft dir aber auch ganz oft beim Lösen von quadratischen Gleichungen.
Quadratische Gleichungen lösen
Wenn deine quadratische Gleichungen
die Form 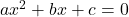 hat, kannst du sie mit quadratischen Ergänzen lösen
.
hat, kannst du sie mit quadratischen Ergänzen lösen
.
Willst du beispielsweise die Nullstellen
einer quadratischen Funktion
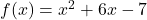 berechnen, kommst du mit quadratischer Ergänzung zum Ziel. Wenn du deine quadratische Gleichung nämlich wie die 1. binomischen Formel
schreibst, ist das Wurzelziehen sehr viel leichter.
berechnen, kommst du mit quadratischer Ergänzung zum Ziel. Wenn du deine quadratische Gleichung nämlich wie die 1. binomischen Formel
schreibst, ist das Wurzelziehen sehr viel leichter.
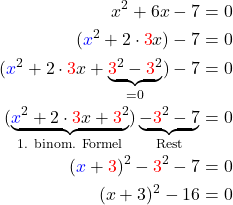
Diesen Term kannst du nun einfach nach x auflösen, indem du -16 auf die andere Seite bringst und die Wurzel ziehst. Die Wurzeln kann ein positives (+4) aber auch ein negatives Vorzeichen (-4) haben. Du bekommst also zwei Lösungen heraus:
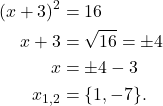
Die Nullstellen von deiner Funktion f(x) liegen also bei x1=1 und x2=-7.
Scheitelpunktform bestimmen
Auf die gleiche Weise kannst du quadratische Funktionen von Normalform (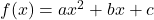 ) in Scheitelpunktform
(
) in Scheitelpunktform
(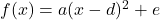 ) bringen. Das ist sehr praktisch, weil du die Koordinaten des Scheitels S(d|e) direkt aus der Formel ablesen kannst.
) bringen. Das ist sehr praktisch, weil du die Koordinaten des Scheitels S(d|e) direkt aus der Formel ablesen kannst.
Wo ist der Scheitelpunkt deiner Funktion f(x)=x2+2x-3?
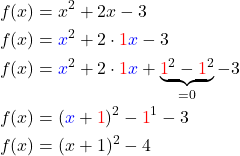
In der Scheitelpunktform (x+1)2-4 kannst du direkt ablesen, dass dein Scheitelpunkt bei (-1|-4) liegt. Du fragst dich warum dein Scheitelpunkt bei x=-1 und nicht bei x=+1 liegt? Das liegt daran, dass die Scheitelpunkfrom a(x-d)2+e mit eine Minus in der Klammer definiert ist. Hier muss d also -1 sein, damit in der Klammer ein Plus stehen kann.
Scheitelpunktform
Gut gemacht! Du weißt jetzt, wie du mit der quadratische Ergänzung quadratische Funktionen f(x) = ax² + bx + c in die Scheitelpunktform f(x) = a(x-d)+e umwandelst. Wir haben dir auch ein passendes Video zur Scheitelpunktform vorbereitet. Schaue gleich mal rein!
