Video

Quiz

Hier geht's zum Video „Schnittpunkt zweier Geraden“

Hier geht's zum Video „Mitternachtsformel“

Hier geht's zum Video „Nullstellen berechnen“

Schnittpunkt berechnen

Wichtige Inhalte in diesem Video

Schnittpunkt berechnen einfach erklärt

Schnittpunkt berechnen – lineare Funktionen

Schnittpunkt berechnen – lineare und quadratische Funktion

Du willst wissen, wie du den Schnittpunkt von Funktionen ganz leicht berechnen kannst? Dann bist du hier genau richtig. Wenn du dich lieber zurücklehnst anstatt lange Texte zu lesen, dann klick doch einfach auf unser Video hier.

Inhaltsübersicht

Schnittpunkt berechnen einfach erklärt

im Videozur Stelle im Video springen

Der Schnittpunkt ist die Stelle im Koordinatensystem, an der sich zwei Funktionsgraphen schneiden.

Schnittpunkt, Schnittpunkt berechnen, Schnittpunkte berechnen, Schnittpunkt lineare Funktionen, Was ist ein Schnittpunkt — Was ist ein Schnittpunkt?

Wenn du die Graphen vor dir hast, kannst du den Schnittpunkt natürlich einfach ablesen – hier wäre er S(1|2). Aber was, wenn du den Schnittpunkt berechnen sollst?

Da die Funktionen f(x) und g(x) an ihrem Schnittpunkt gleich sein sollen, musst du sie gleich setzen.

$\begin{align*}f(x) &= g(x) \\2x &= x+1\end{align*}$

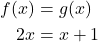
Dann kannst du nach x auflösen, um den x-Wert des Schnittpunktes zu bestimmen.

$\begin{align*}2x &= x+1 \qquad |-x \\x &= \textcolor{magenta}{1}\end{align*}$

Anschließend kannst du dein x in eine der beiden Funktionen einsetzen und kommst so zu dem y-Wert des Schnittpunktes.

f(1) = 2⋅1 = 2

Du siehst: du hast den Schnittpunkt S(1|2) jetzt auch rechnerisch bestimmen können!

Schnittpunktberechnung in 3 Schritten

Setze beide Funktionen gleich.
Löse nach x auf.
Setze x in eine der beiden Funktionen ein, um y zu berechnen.

Eine ausführlichere Erklärung und viele anschauliche Beispiele zur Schnittpunktberechnung bei verschiedenen Funktionen siehst du jetzt.

Schnittpunkt berechnen – lineare Funktionen

im Videozur Stelle im Video springen

Am einfachsten lassen sich die Schnittpunkte linearer Funktionen , also von Geraden, bestimmen. Ein kurzes Beispiel dazu hast du ja schon gesehen.

Probiere die Vorgehensweise jetzt gleich mal selber an diesem Beispiel aus und bestimme den Schnittpunkt:

f(x) = 2x-4 und g(x) = -x+5

Dazu gehst du wie beschrieben vor:

Zuerst setzt du die Funktionen gleich.
$\begin{align*}f(x) &= g(x) \\2x-4 &= -x+5\end{align*}$
Löse dann nach x auf .
$\begin{align*}2x-4 &= -x+5 &| +x \\3x-4 &= 5 &| +4 \\3x &= 9 &| :3 \\ x &= \textcolor{magenta}{3}\end{align*}$
Setze x in eine der beiden Funktionen ein. Dabei ist es egal, in welche der beiden Funktionen du x einsetzt, schließlich haben sie an der Stelle ja den gleichen Wert.

f(3) = 2⋅3-4 = 2

Das heißt: Der Schnittpunkt liegt bei S(3|2)! Das kannst du auch auf dem Bild sehen:

Schnittpunkt, Schnittpunkt berechnen, Schnittpunkte berechnen, lineare Funktionen Schnittpunkt berechnen, was ist ein Schnittpunkt, Funktionen gleichsetzen — Schnittpunkt linearer Funktionen

Schau dir jetzt noch ein Beispiel an. Hier sollst du den Schnittpunkt dieser Funktionen berechnen:

f(x) = -x+7 und g(x) = -x+5

Setze die Funktionen gleich.
$\[\]$

$\begin{align*}f(x) &= g(x) \\-x+7 &= -x+5\end{align*}$
Löse nach x auf.
$\begin{align*}-x+7 &= -x+5 \qquad |+x \\\textcolor{red}{7} &\textcolor{red}{= 5}\end{align*}$

Das ist offensichtlich falsch! Da du rechnerisch keinen Schnittpunkt bestimmen kannst, heißt das, dass es gar keinen Schnittpunkt gibt.

Das siehst du auch, wenn du dir die Graphen der Funktionen anschaust: Da die Geraden die selbe Steigung haben, schneiden sie sich nie. Stattdessen sind sie parallel.

Schnittpunkt, Schnittpunkt berechnen, Schnittpunkte berechnen, lineare Funktionen Schnittpunkt berechnen, Funktionen gleichsetzen, Schnittpunkt parallele Geraden — parallele Geraden haben keinen Schnittpunkt

Merke

Einen Schnittpunkt gibt es nur, wenn die Steigung der Funktionsgleichungen unterschiedlich ist:

z. B. f(x) = 2x + 1 und g(x) = 3x + 2.

Haben zwei Funktionen die gleiche Steigung, sind sie entweder echt parallel (keinSchnittpunkt):

z. B. f(x) = 2x + 2 und g(x) = 2x + 5

oder identisch (unendlich viele Schnittpunkte):

z.B. f(x) = 3x – 4 und g(x) = 3x – 4

Wenn du also bei zwei linearen Funktionen die gleiche Steigung entdeckst, kannst du dir die Schnittpunktberechnung auch sparen!

Super, jetzt weißt du, wie man die Schnittpunkte linearer Funktionen bestimmt. Aber wie sieht die Schnittpunktberechnung bei quadratischen Funktionen aus?

Schnittpunkt berechnen – lineare und quadratische Funktion

im Videozur Stelle im Video springen

Wenn du den Schnittpunkt einer linearen und quadratischen Funktion bestimmen möchtest, gehst du wie gewohnt vor. Nur die Auflösung nach x kann noch einen Schritt mehr erfordern.

Schau dir dazu direkt folgende Funktionsgleichungen an:

f(x) = x und g(x) = x²-4x+4

Setze die Funktionen gleich.
$\begin{align*}f(x) &= g(x) \\x &= x^2-4x+4\end{align*}$
Löse nach x auf. Da hier ein x²und ein x dabei sind, kannst du die Gleichung nicht mehr so leicht durch Umformungen nach x auflösen. Stattdessen musst du hier die Mitternachtsformel verwenden. Dazu brauchst du die Form $0 = \textcolor{red}{a}x^2+\textcolor{blue}{b}x+\textcolor{teal}{c}$ .
$\[\]$

$\begin{align*}x &= x^2-4x+4 \qquad |-x \\0 &= \textcolor{red}{1}x^2\textcolor{blue}{-5}x+\textcolor{teal}{4}\end{align*}$
Jetzt kannst die Mitternachtsformel anwenden:
$x_{1,2} = \frac{-\textcolor{blue}{b}\pm\sqrt{\textcolor{blue}{b}^2-4 \textcolor{red}{a} \textcolor{teal}{c}}}{2 \textcolor{red}{a}} = \frac{- \textcolor{blue}{(-5)}\pm\sqrt{\textcolor{blue}{(-5)}^2-4\cdot \textcolor{red}{1} \cdot \textcolor{teal}{4}}}{2\cdot \textcolor{red}{1}} =\frac{5\pm3}{2}$

$\rightarrow x_1 = 1,\qquad x_2 = 4$
Du siehst, dass du hier zwei mögliche Lösungen für x hast! Das bedeutet, die Funktionen schneiden sich auch zwei mal.
$\[\]$
Setze deine zwei Ergebnisse für x in eine der beiden Funktionen ein.

f(1) = 1 f(4) = 4

Das bedeutet: Deine zwei Schnittpunkte sind S₁(1|1) und S₂(4|4).

Genau das kannst du auch an den Graphen sehen:

Schnittpunkt, Schnittpunkt berechnen, Schnittpunkte berechnen, Funktionen gleichsetzen, Schnittpunkt lineare und quadratische Funktion — Schnittpunkt berechnen lineare und quadratische Funktion

Schnittpunkt zweier quadratischer Funktionen

Wie du die Schnittpunkte von einer linearen und einer quadratischen Funktion bestimmen kannst, weißt du jetzt. Die Schnittpunktberechnung von zwei quadratischen Funktionen stellt dann auch kein Problem mehr für dich dar!

Probier das doch gleich mal an diesen quadratischen Funktionen aus und berechne den Schnittpunkt:

f(x) = x²+1 und g(x) = 2x²

Setze die Funktionen gleich.
$\begin{align*}f(x) &= g(x) \\x^2+1 &= 2x^2\end{align*}$
Löse nach x auf. Da du hier kein x dabei hast, kannst diese Gleichung auch ohne Mitternachtsformel und nur mit Umformungen lösen.
$\[\]$

$\begin{align*}x^2+1 &= 2x^2 \qquad |-x^2 \\1 &= x^2 \qquad | \sqrt{...} \\ \rightarrow x_1 &= \textcolor{magenta}{-1} \qquad x_2 = \textcolor{orange}{1}\end{align*}$
Setze die 2 Punkte in eine der beiden Funktionen ein.

f(-1) = (-1)²+1 = 2 f(1) = 1²+1 = 2

Laut der Schnittpunktberechnung hast du also Schnittpunkte bei S₁(-1|2) und S₂(1|2). Das kannst du auch am Graphen sehen:

Schnittpunkt, Schnittpunkt berechnen, Schnittpunkte berechnen, Funktionen gleichsetzen, Schnittpunkt berechnen quadratische Funktion — Schnittpunkt berechnen quadratische Funktion

Schnittpunkt berechnen Vektoren

Geraden kannst du auch im dreidimensionalen Raum mithilfe von Vektoren darstellen. Zwei Geraden werden dort so dargestellt:

$f:\vec{x}=\vec{A} + \lambda \cdot \vec{u} \qquad \qquad g:\vec{x} = \vec{B} + \mu \cdot \vec{v}$

Dabei sind $\vec{A}$ und $\vec{B}$ Ortsvektoren und $\vec{u}$ und $\vec{v}$ die Richtungsvektoren .

Für die Schnittpunktberechnung der Geraden f und g im dreidimensionalen Raum gehst du am besten so vor:

Überprüfe, ob die Richtungsvektoren $\vec{u}$ und $\vec{v}$ Vielfache voneinander sind.
$\[\]$
Falls ja: Die Richtungsvektoren sind dann linear abhängig . Das bedeutet, die Vektoren zeigen in die gleiche Richtung. Die Geraden sind also entweder identisch oder echt parallel.
$\[\]$
Um das zu überprüfen, kannst du den Ortsvektor von g mit f gleichsetzen und prüfen, ob du $\lambda$ eindeutig bestimmen kannst. Ist das der Fall, dann sind sie identisch.
$\[\]$
Falls nein: Die Geraden haben dann entweder einen Schnittpunkt oder keinen Schnittpunkt – solche Geraden nennt man dann windschief. Hier kannst du dann bei Schritt 2 weiter machen und versuchen, den Schnittpunkt zu berechnen.
$\[\]$
Setze die beiden Geradengleichungen gleich und löse das dazugehörige Gleichungssystem nach $\lambda$ und $\mu$ auf.
$\[\]$
Setze $\lambda$ in die Geradengleichung f ein und bestimme so den Schnittpunkt.

Beispiel:

Du sollst den Schnittpunkt dieser Geraden in Vektordarstellung bestimmen:

$\left( \begin{matrix}1 \\ 0\\0\end{matrix} \right)+ \lambda \cdot \left( \begin{matrix}2 \\ 0\\ 4 \end{matrix} \right) = \left( \begin{matrix}2\\ -1\\3 \end{matrix} \right)+ \mu \cdot \left( \begin{matrix}0 \\ 1\\ -1 \end{matrix} \right)$

Überprüfe zuerst, ob die Richtungsvektoren $\vec{u} = \left( \begin{matrix}2 \\ 0\\ 4 \end{matrix} \right)$ und $\vec{v} = \left( \begin{matrix}0 \\ 1\\ -1 \end{matrix} \right)$ Vielfache voneinander sind. Hier ist das nicht der Fall, denn du kannst keine Zahl finden, mit der du $\vec{v}$ so multiplizieren kannst, dass du $\vec{u}$ rausbekommst.
$\[\]$
Also sind die Geraden nicht parallel, sondern haben entweder einen Schnittpunkt oder sind windschief zueinander.
$\[\]$
Setze die beiden Geradengleichungen gleich
$\left( \begin{matrix}1 \\ 0\\0\end{matrix} \right)+ \lambda \cdot \left( \begin{matrix}2 \\ 0\\ 4 \end{matrix} \right) = \left( \begin{matrix}2\\ -1\\3 \end{matrix} \right)+ \mu \cdot \left( \begin{matrix}0 \\ 1\\ -1 \end{matrix} \right)$
und löse dann das dazugehörige Gleichungssystem nach $\lambda$ und $\mu$ auf.
$\begin{align*}1 + 2\cdot \lambda &= 2 \\0 &= -1 + \mu \\ 4\lambda &= 3-\mu\end{align*}$

$\[\]$
Aus der ersten Zeile folgt direkt, dass $\lambda = \frac{1}{2}$ . Aus der zweiten Zeile kannst du sofort ablesen, dass $\mu = 1$ gelten muss.
$\[\]$
Wenn du das in die dritte Zeile einsetzt, erhältst du 2 = 2. Das ist immer wahr! Also haben die Geraden einen Schnittpunkt und sind nicht windschief.
$\[\]$
Jetzt kannst du den Schnittpunkt ganz leicht berechnen, indem du $\lambda$ in die Geradengleichung f einsetzt. $\left( \begin{matrix}1 \\ 0\\0\end{matrix} \right)+ \frac{1}{2} \cdot \left( \begin{matrix}2 \\ 0\\ 4 \end{matrix} \right) = \left( \begin{matrix} 2 \\ 0 \\ 2 \end{matrix} \right).$

Dein Schnittpunkt liegt also bei 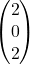$\left( \begin{matrix} 2 \\ 0 \\ 2 \end{matrix} \right)$ .

Schnittpunkt, Schnittpunkt berechnen, Schnittpunkte berechnen, Schnittpunkt berechnen Vektor — Schnittpunkt im dreidimensionalen Raum

Schnittpunkt berechnen — kurz & knapp

Um den Schnittpunkt von zwei Funktionen zu berechnen, setzt du ihre Funktionsterme gleich und formst die Gleichung nach x um. Für die Graphen f(x) = 2x und g(x) = x+3 sind die Koordinaten des Schnittpunkts S(x₀|f(x₀)) = S(2|4).

Quiz zum Thema Schnittpunkt berechnen

Nullstellen berechnen

Super, jetzt weißt du, wie du bei verschiedenen Funktionsarten den Schnittpunkt berechnen kannst. Oft sind aber nicht nur Schnittpunkte, sondern auch Nullstellen von Funktionen gefragt. Wie du die berechnest, siehst du in unserem Video dazu.

Zum Video: Nullstellen berechnen

zur Videoseite: Schnittpunkt berechnen

Beliebte Inhalte aus dem Bereich Funktionen

Schnittpunkte mit den Koordinatenachsen

Schnittpunkt zweier Geraden

Schnittpunkte zweier Funktionen

Schnittpunkt berechnen

Schnittwinkel berechnen

Steigungswinkel

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .