Was ist der Schnittwinkel zwischen zwei Geraden?

Der Schnittwinkel zwischen zwei Geraden ist der Winkel, der an ihrem Schnittpunkt entsteht. Wenn sich zwei Geraden schneiden, entstehen vier Winkel, wobei jeweils gegenüberliegende Winkel gleich groß sind. Meist ist mit dem Schnittwinkel α der kleinere Winkel gemeint, also der Winkel kleiner als 90°.

Wann schneiden sich zwei Geraden überhaupt in einem Punkt?

Zwei Geraden schneiden sich genau dann in einem Punkt, wenn sie unterschiedliche Steigungen haben. Haben beide Geraden die gleiche Steigung, sind sie parallel und es gibt keinen Schnittpunkt. Konkret sind und parallel, weil beide die Steigung 2 besitzen.

Wie setze ich die Steigungen in die Schnittwinkel-Formel richtig ein?

Du setzt die beiden Steigungen und in ein und berechnest dann mit . Steht vor dem keine Zahl, nimm 1, bei „“ ist die Steigung −1.

Warum brauche ich bei der Schnittwinkel-Formel den Betrag?

Den Betrag brauchst du, damit beim Rechnen kein negatives Ergebnis in der Klammer steht und dadurch kein negativer Winkel herauskommt. Der Betrag entfernt das Vorzeichen, zum Beispiel wird aus die positive Zahl 2. So erhältst du einen Winkel als positive Größe.

Was mache ich, wenn mein Taschenrechner bei der Formel „Error“ zeigt?

Wenn der Taschenrechner „Error“ zeigt, prüfe, ob gilt. Dann stehen die Geraden senkrecht aufeinander, der Schnittwinkel beträgt 90° und die Formel kann nicht angewendet werden. Außerdem muss der Taschenrechner für Grad auf DEG eingestellt sein.

Video

Quiz

Hier geht's zum Video „Winkelsumme“

Hier geht's zum Video „Steigungswinkel“

Schnittwinkel berechnen

Wichtige Inhalte in diesem Video

Schnittwinkel einfach erklärt

(00:13)

Schnittwinkel mit den Koordinatenachsen

(03:32)

Was genau ein Schnittwinkel ist und wie du ihn bei linearen und allgemeinen Funktionen bestimmen kannst, erfährst du hier und in unserem Video !

Inhaltsübersicht

Schnittwinkel einfach erklärt

im Videozur Stelle im Video springen

(00:13)

Ein Schnittwinkel ist ein Winkel zwischen zwei Funktionen, die sich schneiden. Du hast bestimmt schon einmal gesehen, wie sich zwei Geraden schneiden und vier Schnittwinkel entstehen. In diesem Fall sind die jeweils gegenüberliegenden Winkel gleich groß. Der für dich relevante Schnittwinkel α ist aber meist der kleinere Winkel (< 90°).

Alpha und Beta sind Nebenwinkel und ergeben zusammen 180 Grad: α + β = 180°.

Schnittwinkel berechnen, schnittwinkel bestimmen, schnittwinkelproblem, schnittwinkel zweier geraden, winkel zwischen zwei geraden — Schnittwinkel zwischen zwei Geraden

Damit aber erstmal ein Winkel zwischen zwei Geraden entstehen kann, brauchst du einen Schnittpunkt. Zwei Geraden schneiden sich, wenn sie eine unterschiedliche Steigung besitzen.

Die Geraden y = 2x-1 und y = 2x+4 haben zum Beispiel die gleiche Steigung m₁ = m₂. Sie sind parallel zueinander und erfüllen daher die Voraussetzung nicht.

Schnittwinkel berechnen — Formel

Wie kannst du den Schnittwinkel α nun berechnen? Du hast beispielsweise zwei Geraden gegeben. Relevant sind hier die beiden Steigungen m₁ und m₂, die du in die folgende Formel einsetzt. Das Ergebnis ist der gesuchte Schnittwinkel α.

$tan(\textcolor{blue}{\alpha})=\left|\frac{\textcolor{red}{m_{1}} - \textcolor{cyan}{m_{2}}}{1+\textcolor{red}{m_{1}}\cdot \textcolor{cyan}{m_{2}}}\right|$

Die Betragszeichen | brauchst du, damit das Vorzeichen der Zahl wegfällt und kein negativer Winkel herauskommt: |-2| = 2.

Damit du direkt los rechnen kannst, haben wir dir die Formel auch schon nach α umgestellt :

$\textcolor{blue}{\alpha}=tan^{-1} \left(\left| \frac{\textcolor{red}{m_{1}} - \textcolor{cyan}{m_{2}}}{1+\textcolor{red}{m_{1}}\cdot \textcolor{cyan}{m_{2}}} \right|\right)$

Vorsicht: Damit du dein Ergebnis in Grad rausbekommst, musst du den Taschenrechner auf Degree (DEG) stellen. Den Arcustangens selbst findest du auf deinem Taschenrechner meistens als tan^-1 oder arctan.

Studyflix vernetzt: Hier ein Video aus einem anderen Bereich

Schnittwinkel berechnen — Beispiele

Im Folgenden sind jeweils zwei Geraden gegeben, die sich schneiden. Sie haben also einen Schnittpunkt und erfüllen damit die Voraussetzung dafür, dass es einen Schnittwinkel α gibt.

Beispiel 1:

g: y = -0,5x – 1

h: y = 3x

Um den Schnittwinkel α zu bestimmen, setzt du die Steigungen der Funktionen in die Formel ein:

$\textcolor{blue}{\alpha}=tan^{-1} \left(\left| \frac{\textcolor{red}{(-0,5)} - \textcolor{cyan}{3}}{1+\textcolor{red}{(-0,5)}\cdot \textcolor{cyan}{3}} \right|\right)=81,87^\circ$

Beispiel 2:

g: y = 2x + 4

h: y = –x + 3

Wenn vor dem x keine Zahl steht, dann denke dir eine 1 oder bei einem Minus eine -1 dazu.

Um den Schnittwinkel α zu bestimmen, setzt du die Steigungen der Funktionen in die Formel ein:

$\textcolor{blue}{\alpha}=tan^{-1} \left(\left| \frac{\textcolor{red}{2} - \textcolor{cyan}{(-1)}}{1+\textcolor{red}{2}\cdot \textcolor{cyan}{(-1)}} \right|\right)=71,57^\circ$

Ausnahme: 90 Grad Winkel

Wenn m₁· m₂= -1 ergibt, dann schneiden sich die Geraden in einem 90 Grad Winkel (rechter Winkel). Das bedeutet, dass sie senkrecht aufeinander stehen und die Formel nicht angewendet werden kann. Dein Taschenrechner wird dich aber mit einem „Error“ darauf hinweisen. In diesem Fall kannst du dann mit m₁ · m₂ = -1 überprüfen, ob der Fehler daher kommt. Du weißt dann direkt, dass der Schnittwinkel 90 Grad beträgt.

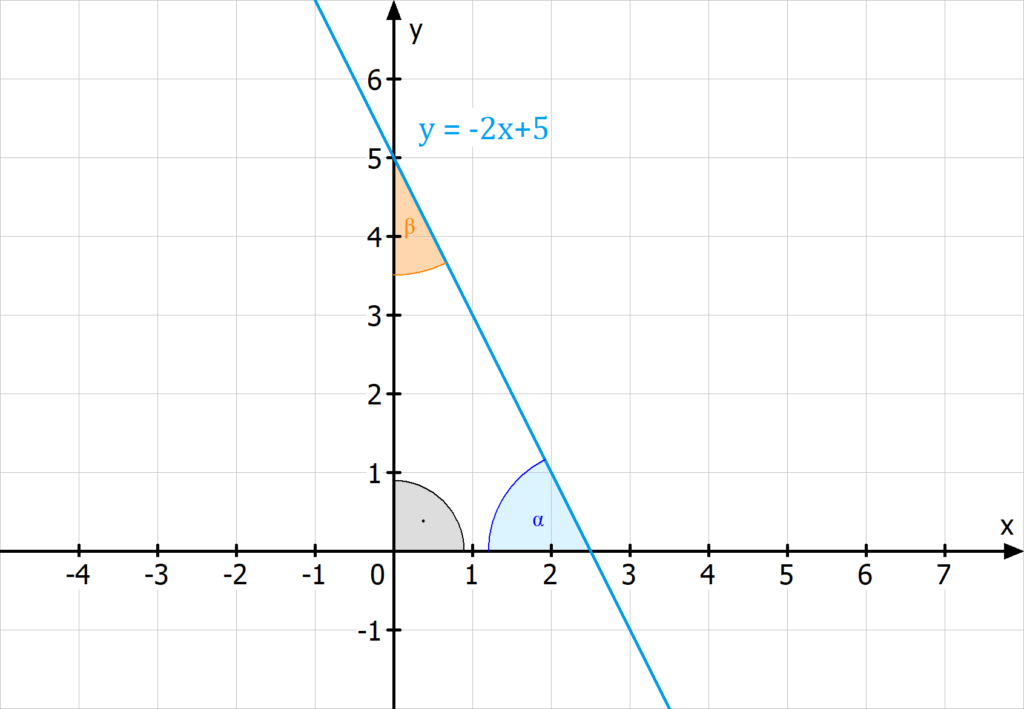
Schnittwinkel mit den Koordinatenachsen

im Videozur Stelle im Video springen

(03:32)

Ein Schnittwinkel kann nicht nur zwischen zwei Geraden, sondern auch zwischen einer Geraden und den Koordinatenachsen entstehen. Es bildet sich ein rechtwinkliges Dreieck.

Schnittwinkel mit koordinatenachsen, Schnittwinkel berechnen, schnittwinkel bestimmen, schnittwinkelproblem, schnittwinkel zweier geraden, winkel zwischen zwei geraden — Schnittwinkel mit den Koordinatenachsen

Um hier die Schnittwinkel zu berechnen, schau dir die folgenden Schritte an:

Schritt: Schnittwinkel α mit der x-Achse α = tan^-1 (|m|)

Der Schnittwinkel mit der x-Achse wird auch Steigungswinkel genannt.
Schritt: Schnittwinkel β mit der y-Achse β = 180° – 90° – α
Da ein Dreieck immer eine Winkelsumme von 180° hat, kannst du den rechten Winkel (90°) sowie den Winkel α davon abziehen. So erhältst du den Winkel β.

Beispiel: y = -2x + 5

1. Schritt: α = tan^-1 (|-2|) = tan^-1 (2) = 63,43°

2. Schritt: β = 180° – 90° – 63,43° = 26,57°

Schnittwinkel von Funktionen

Andere Funktionen wie Parabeln können auch mit Geraden einen Schnittwinkel bilden. Zur Berechnung der Schnittwinkel brauchst du die Steigungen beider Funktionen. Bei einer Parabel kannst du die Steigung aber nicht direkt ablesen. In diesem Fall bildest du zuerst die Ableitung . Vielleicht hast du schonmal gehört, dass die Ableitung die Steigung der Tangente an einem bestimmten Punkt darstellt. Hier schaust du dir die Steigung in dem Schnittpunkt an. Der Schnittwinkel entsteht dann zwischen der Tangenten in dem Schnittpunkt und der Geraden.

Schnittwinkel einer Geraden und Parabel, Schnittwinkel berechnen, schnittwinkel bestimmen, schnittwinkelproblem, schnittwinkel zweier geraden, winkel zwischen zwei geraden — Schnittwinkel einer Parabel und einer Geraden

Schneiden sich die Gerade g und die Parabel f im Punkt P (a|f(a)) kannst du folgende Formel anwenden:

$\textcolor{blue}{\alpha}= | tan^{-1} (\textcolor{red}{f'(a)}) - tan^{-1} (\textcolor{cyan}{g'(a)}) |$

Beispielrechnung für den Schnittwinkel

g: g(x) = 2x + 5

f: f(x) = x²+ 2

Die Gerade g und die Parabel f schneiden sich in den Punkten P (-1|3) und Q (3|11). Du kannst nun für beide Punkte einen Schnittwinkel berechnen. Im Beispiel arbeitest du mit dem Punkt P.

Zuerst leitest du die Parabel f und die Gerade g ab:

f'(x) = 2x

g'(x) = 2

Dann setzt du die x-Koordinate des Schnittpunktes P (-1|3) ein:

f'(-1) = 2 · (-1) = -2

g'(-1) = 2

Nun hast du alle Komponenten, um die oben genannte Formel anzuwenden:

$\textcolor{blue}{\alpha}= |tan^{-1} (\textcolor{red}{(-2)}) - tan^{-1} (\textcolor{cyan}{2})|=126,87^\circ$

Wie du im ersten Kapitel bereits gelernt hast, ist der kleinere Winkel der gesuchte Schnittwinkel. Deswegen musst du von 180° noch die 126,87° abziehen.

180° – 126,87° = 53,13°

Schnittwinkel berechnen — häufigste Fragen

(ausklappen)

Was ist der Schnittwinkel zwischen zwei Geraden?

Der Schnittwinkel zwischen zwei Geraden ist der Winkel, der an ihrem Schnittpunkt entsteht. Wenn sich zwei Geraden schneiden, entstehen vier Winkel, wobei jeweils gegenüberliegende Winkel gleich groß sind. Meist ist mit dem Schnittwinkel α der kleinere Winkel gemeint, also der Winkel kleiner als 90°.
Wann schneiden sich zwei Geraden überhaupt in einem Punkt?

Zwei Geraden schneiden sich genau dann in einem Punkt, wenn sie unterschiedliche Steigungen haben. Haben beide Geraden die gleiche Steigung, sind sie parallel und es gibt keinen Schnittpunkt. Konkret sind und parallel, weil beide die Steigung 2 besitzen.
Wie setze ich die Steigungen in die Schnittwinkel-Formel richtig ein?

Du setzt die beiden Steigungen und in $\tan(\alpha)=\left|\frac{m_1-m_2}{1+m_1\cdot m_2}\right|$ ein und berechnest dann $\alpha$ mit $\alpha=\tan^{-1}(\dots)$ . Steht vor dem keine Zahl, nimm 1, bei
„“ ist die Steigung −1.
Warum brauche ich bei der Schnittwinkel-Formel den Betrag?

Den Betrag brauchst du, damit beim Rechnen kein negatives Ergebnis in der Klammer steht und dadurch kein negativer Winkel herauskommt. Der Betrag entfernt das Vorzeichen, zum Beispiel wird aus die positive Zahl 2. So erhältst du einen Winkel als positive Größe.
Was mache ich, wenn mein Taschenrechner bei der Formel „Error“ zeigt?

Wenn der Taschenrechner „Error“ zeigt, prüfe, ob $m_1\cdot m_2=-1$ gilt. Dann stehen die Geraden senkrecht aufeinander, der Schnittwinkel beträgt 90° und die Formel kann nicht angewendet werden. Außerdem muss der Taschenrechner für Grad auf DEG eingestellt sein.

Steigungswinkel

Nachdem du das Schnittwinkelproblem gelöst hast und nun weißt, wie du den Schnittpunkt zweier Geraden oder einer Geraden und einer Parabel bestimmst, kannst du dir auch anschauen, wie ein Steigungswinkel entsteht. Hier geht’s zum Video !