Ganze Zahlen
Hier erfährst du alles, was du über die Menge der ganzen Zahlen wissen musst. Schau dir auch unser passendes Video an!
Inhaltsübersicht
Was sind ganze Zahlen?
Zu den ganzen Zahlen gehören die natürlichen Zahlen
, die Null und die negativen Zahlen. Das sind zum Beispiel 13, 0 und -4. Sie müssen immer „ganz“ sein: Zahlen mit einem Komma und Nachkommastellen — wie zum Beispiel 1,5 — zählst du deshalb nicht dazu.
Die Zahlen haben immer ein Vorzeichen, entweder ein „+“ oder ein „–„. Das „+“ lässt du aber meistens weg.
Du kannst die Menge der ganzen Zahlen mathematisch als Z mit Doppelstrich schreiben:
![Rendered by QuickLaTeX.com \[ \mathbb{Z} = \{\textcolor{red}{\dots, -3, -2, -1}, 0, \textcolor{teal}{1, 2, 3, \dots}\} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-9ce38d116132a83d4bb53bf5b981fa7a_l3.png)
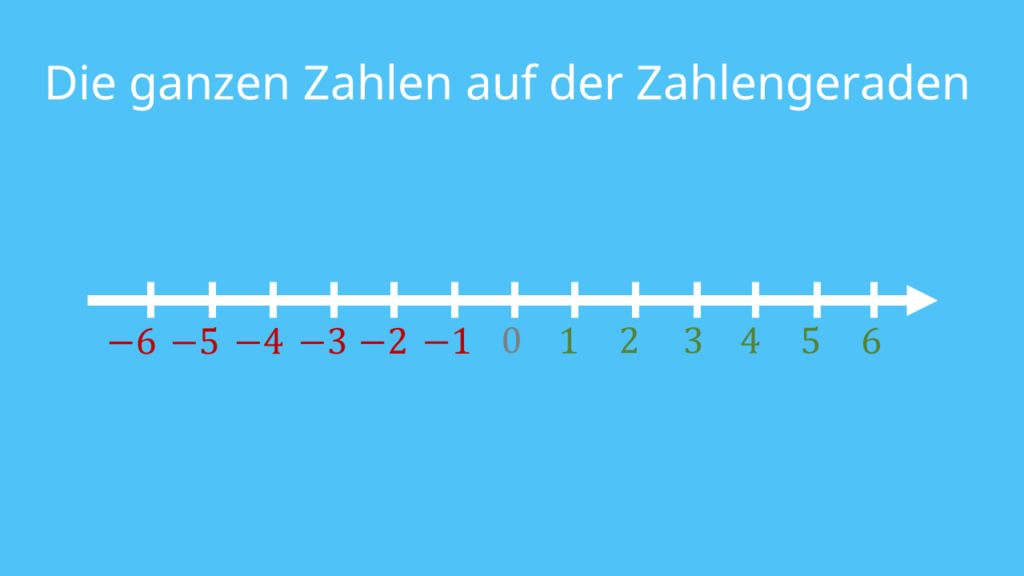
Ganze Zahlen auf der Zahlengeraden
Du kannst positive und negative Zahlen auf einer Zahlengeraden von klein nach groß anordnen. Die negativen Zahlen stehen dabei links von der 0 und die positiven rechts. Alle Zahlen haben immer den gleichen Abstand voneinander.
Je weiter rechts eine Zahl ist, desto größer ist sie. Die -2 ist also größer als die -5. Du kannst dir das mithilfe der Temperatur merken: Wenn es draußen -2 Grad hat, ist das wärmer, als wenn es -5 Grad hat — die Temperatur ist also größer.
Übrigens: Die Zahlen mit dem jeweils anderen Vorzeichen, also zum Beispiel die 5 und die -5, nennst du auch Gegenzahlen. Die Menge  enthält also die natürlichen Zahlen, ihre Gegenzahlen und die 0. Manchmal bezeichnest du die Gegenzahl einer natürlichen Zahl auch als unnatürliche Zahl.
enthält also die natürlichen Zahlen, ihre Gegenzahlen und die 0. Manchmal bezeichnest du die Gegenzahl einer natürlichen Zahl auch als unnatürliche Zahl.
Aber wie kannst du mit diesen Zahlen rechnen? Das erfährst du jetzt!
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Rechnen mit ganzen Zahlen
Du kannst positive Zahlen und ihre Gegenzahlen multiplizieren, dividieren, subtrahieren und addieren. Schau dir dazu ein paar Beispiele mit den Grundrechenarten an.
Plus und Minus Rechnen
Löse die Aufgaben durch Addition und Subtraktion!

Schaue dir zuerst  an. Du startest auf deinem Zahlenstrahl bei -5 und gehst 2 Schritte nach rechts. Du kommst bei -5+2=-3 heraus.
an. Du startest auf deinem Zahlenstrahl bei -5 und gehst 2 Schritte nach rechts. Du kommst bei -5+2=-3 heraus.
Wie rechnest du  ? Du beginnst auf dem Zahlenstrahl bei -1. Danach gehst du 1 Schritt nach links. Dein Ergebnis ist also -1-1=-2.
? Du beginnst auf dem Zahlenstrahl bei -1. Danach gehst du 1 Schritt nach links. Dein Ergebnis ist also -1-1=-2.
Zuletzt rechnest du noch  . Du fängst auf deinem Zahlenstrahl bei +7 an. Jetzt gehst du 4 Schritte nach links und kommst bei +7-4=+3 an.
. Du fängst auf deinem Zahlenstrahl bei +7 an. Jetzt gehst du 4 Schritte nach links und kommst bei +7-4=+3 an.
Mal Rechnen
Wie sieht es mit der Multiplikation mit negativen Zahlen aus? Beim Multiplizieren musst du auf das Vorzeichen aufpassen!
Passe beim Multiplizieren auf die Vorzeichen auf!
- Plus mal Plus ist Plus.
- Plus und Minus ergibt Minus. / Minus und Plus ergibt Minus.
- Minus mal Minus ergibt Plus.
Wir haben dir noch ein paar Beispiele mit Minus mal Plus und Minus mal Minus herausgesucht:

Geteilt Rechnen
Beim Dividieren musst du aufpassen: Du kannst ganze Zahlen nur durcheinander teilen, wenn der Divisor ein Teiler des Dividenden ist.
Auch bei der Division ist das Vorzeichen entscheidend:
- Plus geteilt durch Plus ist Plus.
- Plus und Minus ergibt Minus. / Minus und Plus ergibt Minus.
- Minus geteilt durch Minus ergibt Plus.
Hier kannst du dein Wissen in ein paar Beispielen testen:

Expertenwissen: Teilmengen der ganzen Zahlen
Du kennst schon die Schreibweise mit dem Z-Zeichen:
![Rendered by QuickLaTeX.com \[ \textcolor{olive}{\mathbb{Z}} = \{\dots; -3, -2, -1, 0, 1, 2, 3, \dots\} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-96f397d2422319fb99c5929e9da31b9a_l3.png)
 beinhaltet also alle natürlichen Zahlen
1, 2, 3, … Die kannst du mathematisch mit einem N mit Doppelstrich bezeichnen:
beinhaltet also alle natürlichen Zahlen
1, 2, 3, … Die kannst du mathematisch mit einem N mit Doppelstrich bezeichnen:
![Rendered by QuickLaTeX.com \[ \textcolor{blue}{\mathbb{N}} = \{1, 2, 3, \dots\} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-b74b1a80149e9870ba41e23456172f1a_l3.png)
Möchtest du die 0 noch mit dazunehmen, ergibt sich die Menge:
![Rendered by QuickLaTeX.com \[ \textcolor{teal}{\mathbb{N}_0} = \{0, 1; 2, 3, \dots\} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-cccd0345205961e8835cb1d4a98c1d46_l3.png)
Weil die Menge der natürlichen Zahlen und die 0 komplett in den ganzen Zahlen enthalten sind, kannst du schreiben:
![Rendered by QuickLaTeX.com \[ \textcolor{blue}{\mathbb{N}} \subset \textcolor{olive}{\mathbb{Z}} \, \text{und} \, \textcolor{teal}{\mathbb{N}_0} \subset \textcolor{olive}{\mathbb{Z}} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-638ca17d5a6548d14d80cab587e6a91a_l3.png)
Sprich:  ist eine Teilmenge von
ist eine Teilmenge von 
Es gibt aber noch weitere Teilmengen von  . Du siehst sie in der Tabelle:
. Du siehst sie in der Tabelle:
| Zeichen | Beschreibung der Menge | enthaltene Zahlen |
|
nur positive Zahlen | {1, 2, 3, …} |
|
nur negative Zahlen | {…, -3, -2, -1} |
|
ganze Zahlen ohne 0 | {…, -3, -2, -1, 1, 2, 3, …} |
|
positive Zahlen mit 0 | {0, 1, 2, 3, …} |
|
negative Zahlen mit 0 | {…, -3, -2, -1, 0} |
Rationale Zahlen
Mit rationalen Zahlen kannst du ganze Zahlen durcheinander dividieren, selbst wenn sie keinen gemeinsamen Teiler haben. Schaue dir gleich unser passendes Video an!


![Rendered by QuickLaTeX.com \[\mathbb{Z}^+\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-fa2a65470580dc048030116d3c01af17_l3.png)
![Rendered by QuickLaTeX.com \[\mathbb{Z}^-\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-70dedf31b891eb5e9f65c4601afb8761_l3.png)
![Rendered by QuickLaTeX.com \[\mathbb{Z}^*\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-09ecfbda246db36021f80f7e8eafbbc4_l3.png)
![Rendered by QuickLaTeX.com \[\mathbb{Z}_0^+\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-bd938d5d092434df4c3c0b2c0bca5a24_l3.png)
![Rendered by QuickLaTeX.com \[\mathbb{Z}_0^-\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-5d7f40829cbffac645bd424f2a18ac97_l3.png)