Nullstellen berechnen quadratische Funktion
Du willst wissen, wie du Nullstellen einer quadratischen Funktion berechnen kannst? Und was hat die Mitternachtsformel damit zu tun? Dann ist dieser Artikel und unser Video genau das Richtige für dich!
Inhaltsübersicht
Nullstellen berechnen quadratische Funktion — einfach erklärt
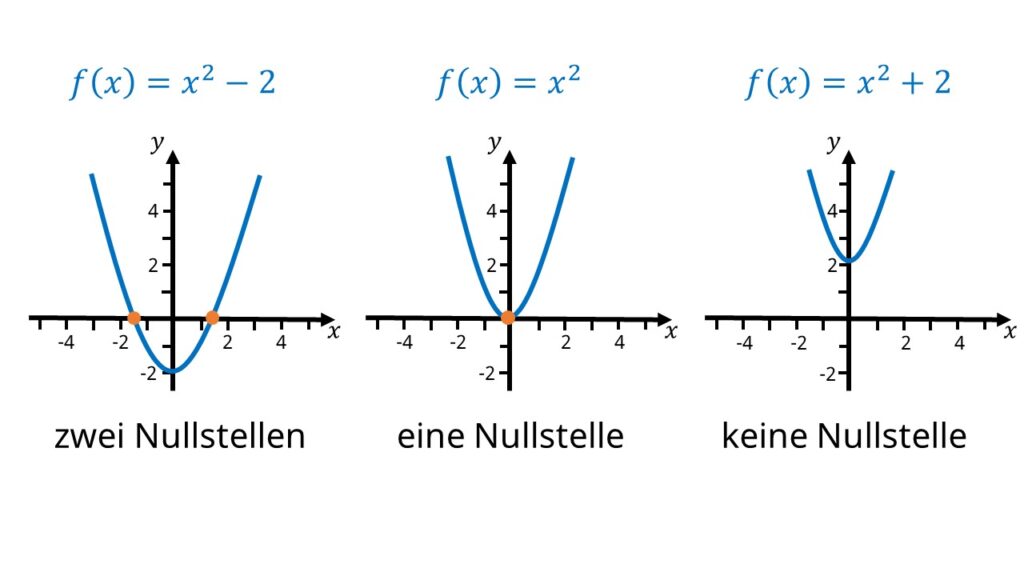
Die Nullstellen einer quadratischen Funktion sind die Punkte, an denen die Funktion die x-Achse schneidet. Eine quadratische Funktion kann zwei, eine oder keine Nullstelle haben.
Die Funktion f(x) = x2 – 2 hat zum Beispiel zwei Nullstellen. f(x) = x2 + 2 hat dagegen gar keine.
Aber wie sieht es mit anderen Parabeln aus, zum Beispiel f(x) = 2x2 + 4x – 6 oder f(x) = x2 + 3x? Um dann die Nullstellen der Parabel zu berechnen, kannst du immer die Mitternachtsformel verwenden. Schau dir gleich an, wie das funktioniert!
Nullstellen mit Mitternachtsformel berechnen
Du kannst die Nullstellen von quadratischen Funktionen f(x) = ax2 + bx – c immer mit der Mitternachtsformel berechnen. Dafür brauchst du nur die Zahl vor dem x2 (a), die Zahl vor dem x (b) und die Zahl ohne x (c).
Die Nullstellen x1 und x2 einer quadratischen Funktion sind:
![Rendered by QuickLaTeX.com \[x_{1/2} = \frac{-\textcolor{blue}{b}\pm\sqrt{\textcolor{blue}{b}^2-4\textcolor{red}{a}\textcolor{teal}{c}}}{2\textcolor{red}{a}}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-1ca07f6f7644a977a725ebd379722545_l3.png)
Schau dir das gleich an einem Beispiel an:
f(x) = 2x2 + 4x – 6
Hier ist a = 2 (Zahl vor dem x2), b = 4 (Zahl vor dem x) und c = -6.
Jetzt gehst du in 3 Schritten vor:
- Schritt 1: Setze die Funktion gleich 0:
2x2 + 4x – 6 = 0
-
Schritt 2: Setze a, b und c in die Mitternachtsformel ein. Achte dabei auf negative Vorzeichen! (hier: –6):
![Rendered by QuickLaTeX.com \[x_{1/2} = \frac{-\textcolor{blue}{4}\pm\sqrt{\textcolor{blue}{4}^2-4\cdot \textcolor{red}{2}\cdot \textcolor{teal}{(-6)}}}{2\cdot \textcolor{red}{a}}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-fd4d992ea16d369a7b5ccdd6374e9d6e_l3.png)
-
Schritt 3: Rechne die Mitternachtsformel einmal mit Plus und einmal mit Minus vor der Wurzel aus:
und![Rendered by QuickLaTeX.com \[x_{1} = \frac{-\textcolor{blue}{4}+\sqrt{\textcolor{blue}{4}^2-4\cdot \textcolor{red}{2}\cdot \textcolor{teal}{(-6)}}}{2\cdot \textcolor{red}{2}} = 1\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-47b6a098ff428d547509a7cc5c155e59_l3.png)
![Rendered by QuickLaTeX.com \[x_{2} = \frac{-\textcolor{blue}{4}-\sqrt{\textcolor{blue}{4}^2-4\cdot \textcolor{red}{2}\cdot \textcolor{teal}{(-6)}}}{2\cdot \textcolor{red}{2}} = -3\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-67377b94c879d8954337916370a43942_l3.png)
Deine beiden Nullstellen der quadratischen Funktion liegen bei x1 = 1 und x2 = -3. Du hast also zwei Nullstellen. Allgemein kannst du dir merken:
- 2 Nullstellen: Unter der Wurzel steht eine positive Zahl.
- 1 Nullstelle: Unter der Wurzel steht 0.
- Keine Nullstelle: Unter der Wurzel steht eine negative Zahl.
Die Zahl unter der Wurzel nennst du auch Diskriminante .
Übrigens: Wenn vor x2 keine Zahl steht, kannst du auch die pq-Formel verwenden, um Nullstellen quadratischer Funktionen zu berechnen. Schau dir gleich unser Video dazu an, um sie genauer kennenzulernen!
Die Mitternachtsformel kannst du bei jeder quadratischen Funktion anwenden. Manchmal gibt es aber einen leichteren Weg, die Nullstellen einer Parabel zu berechnen. Schau dir dazu das Ausklammern und das Wurzelziehen an.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Nullstellen durch Ausklammern (ax2 + bx)
Ausklammern kannst du immer dann, wenn deine Funktion keine Zahl ohne x (c) hat.
Beispiel: f(x) = 2x2 – 4x
Hier gehst du so vor:
- Schritt 1: Setze die Funktion gleich 0:
2x2 – 4x = 0
- Schritt 2: Klammere ein x aus:
x • (2x – 4) = 0
- Schritt 3: Setze die Klammer gleich 0 und löse nach x auf:
2x – 4 = 0 ⇒ x = 2
Die Nullstellen der Parabel sind dann x1 = 2 und x2 = 0. Merk dir, dass die zweite Nullstelle beim Ausklammern immer 0 ist!
Nullstellen durch Wurzelziehen (ax2 und ax2 + c)
Wurzelziehen kannst du dann anwenden, wenn deine Funktion kein x ohne Quadrat hat. Das ist bei diesen Funktionen der Fall:
- f(x) = 2x2 (nur x2, aber kein x ohne Quadrat)
- f(x) = 2x2 – 8 (nur x2 und Zahl ohne x, aber kein x ohne Quadrat)
Schau dir an, wie du die Nullstellen der beiden quadratischen Funktionen berechnen kannst!
Nullstellen der Parabel f(x) = 2x2 berechnen
- Schritt 1: Setze die Funktion gleich 0:
2x2 = 0
-
Schritt 2: Die einzige Nullstelle ist x = 0. Das ist immer so, wenn nur x2 in der Funktion vorkommt, aber kein x und keine Zahl ohne x!
Nullstellen der Parabel f(x) =2x2 – 8 berechnen
- Schritt 1: Setze die Funktion gleich 0:
2x2 – 8 = 0
- Schritt 2: Löse nach x2 auf. Dafür bringst du 8 auf die andere Seite und teilst durch 2.
2x2 – 8 = 0 ⇒ 2x2 = 8 ⇒ x2 = 4
- Schritt 3: Ziehe die Wurzel :
x2 = 4 ⇒ x =  = ± 2
= ± 2
Deine beiden Nullstellen der quadratischen Funktion sind also x1 = -2 und x2 = 2.
- An einer Nullstelle ist der Wert einer quadratischen Funktion gleich 0, also f(x) = 0.
- Eine quadratische Funktion hat keine, eine oder zwei Nullstellen. Sie sind die Lösungen der quadratischen Gleichung ax2 + bx + c = 0.
Um die Nullstellen zu berechnen, brauchst du deshalb die allgemeine Form einer quadratischen Funktion, also f(x) = ax2 + bx + c:
- Setze die Funktionsgleichung gleich 0: ax2 + bx + c = 0
- Du erhältst die Nullstellen x1 und x2 zum Beispiel mit der Mitternachtsformel:
![Rendered by QuickLaTeX.com \[x_{1/2} = \frac{-\textcolor{blue}{b}\pm\sqrt{\textcolor{blue}{b}^2-4\textcolor{red}{a}\textcolor{teal}{c}}}{2\textcolor{red}{a}}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-1ca07f6f7644a977a725ebd379722545_l3.png)
Schnittpunkte quadratischer Funktionen
Bei Nullstellen berechnest du die Schnittpunkte einer quadratischen Funktion mit der x-Achse. Aber was, wenn zwei quadratische Funktionen sich schneiden? Oder eine Parabel und eine Gerade?
Schau dir gleich an einem Beispiel an, wie du dann vorgehst. Du hast die quadratischen Funktionen f(x) = 4x2 + 8 und g(x) = x2 – 9x + 2
- Schritt 1: Setze die beiden Funktionen gleich:
4x2 + 8 = x2 – 9x + 2
- Schritt 2: Bring alles auf eine Seite. Auf der anderen Seite steht dann automatisch eine 0:
3x2 + 9x + 6 = 0
- Schritt 3: Löse die Gleichung wie bei den Nullstellen. Hier kannst du die Mitternachtsformel verwenden. Die beiden Schnittpunkte liegen bei x1 = -1 und x2 = -2.
- Schritt 4: Setze die x-Werte in eine der beiden Funktionen ein. Du erhältst die y-Werte f(x1) = 12 und f(x2) = 24.
Deine Schnittpunkte sind also S1(-1|12) und S2(-2|24).
Das ging dir zu schnell? Dann schau dir gleich unser Video zu Schnittpunkten von Funktionen an!