Video

Quiz

Hier geht's zum Video „Kettenregel“

Hier geht's zum Video „Potenzregel und Faktorregel“

Hier geht's zum Video „Produktregel“

Hier geht's zum Video „Bruch ableiten“

e Funktion

Wichtige Inhalte in diesem Video

e Funktion einfach erklärt

Eigenschaften der e Funktion

Umkehrfunktion der e Funktion

e Funktion ableiten

Integration der e Funktion

In diesem Artikel erklären wir dir alles Wichtige zur e Funktion, samt ihren Eigenschaften, Rechenregeln und vielen Beispielen. Eine tabellarische Zusammenfassung der wichtigsten Punkte findest du am Ende des Artikels.

Du willst direkt sehen, was es mit der e Funktion auf sich hat? Dann schau dir einfach unser Video an.

Inhaltsübersicht

e Funktion einfach erklärt

im Videozur Stelle im Video springen

Die e Funktion ist eine Exponentialfunktion zur Basis $e \approx 2,7182$ . Sie ist in der Mathematik so wichtig, dass sie auch als natürliche Exponentialfunktion bezeichnet wird. Ihre Funktionsgleichung lautet

e Funktion

f(x) = e^x

e Funktion, e^x, exp(x), Funktionsgraph der e Funktion — Funktionsgraph der e Funktion

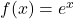
Achtung: Lass dich von dem e nicht verwirren! Dabei handelt es sich um eine ganz normale Zahl, ähnlich wie bei $\pi$ !

Die Zahl e

im Videozur Stelle im Video springen

Die Basis e der natürlichen Exponentialfunktion ist in vielerlei Hinsicht besonders. Entdeckt wurde sie 1748 von dem bedeutenden Mathematiker Leonard Euler, als er versuchte, den Grenzwert einer unendlichen Reihe zu berechnen:

$\sum\limits_{n=0}^\infty \cfrac{1}{n!} = \frac{1}{0!}+ \frac{1}{1!}+ \frac{1}{2!}+ \frac{1}{3!}+\ldots$

$=1+\frac{1}{1 }+\frac{1}{2\cdot 1}+\frac{1}{ 3 \cdot 2\cdot 1}+ \frac{1}{4 \cdot 3 \cdot 2\cdot 1} + \ldots= 2,7182\ldots = e$

Die Fakultät berechnet man immer als $n! = n(n-1)(n-2)(n-3)....\cdot 3\cdot 2 \cdot 1$ . Beispielsweise ist $5! = 5 \cdot 4 \cdot 3\cdot 2 \cdot 1= 120$ , aufpassen musst du lediglich bei 0! = 1

Merke: Die Zahl e hat unendlich viele Nachkommastellen, sie ist also keine rationale Zahl und du kannst sie nicht als Bruch darstellen.

Eigenschaften der e Funktion

im Videozur Stelle im Video springen

Dass die e-Funktion so besonders ist, liegt an verschiedenen Eigenschaften und Merkmalen, die wir dir hier kurz und knapp zusammengefasst vorstellen. Du kannst sie leicht am obigen Funktionsgraphen überprüfen.

In vielen Fällen betrachtest du natürliche Exponentialfunktionen, die aus verketteten Funktionen bestehen. Sie sind dann beispielsweise im Koordinatensystem verschoben oder gestaucht. Diese Fälle behandeln wir exemplarisch unter jedem einzelnen Abschnitt.

Definitions- und Wertebereich

Die e Funktion ist – wie alle Exponentialfunktionen – für alle reellen Zahlen definiert. Sie nimmt jedoch nur positive Werte an.

Definitionsbereich von f(x)=e^x : $\mathbb{D}=\mathbb{R}$

Wertebereich von f(x)=e^x : $\mathbb{W}=\mathbb{R}^+$

Wenn du eine verkettete Exponentialfunktion betrachtest, also beispielsweise

$f(x)=e^{\frac{1}{x^2}$ ,

musst du sowohl den Definitionsbereich als auch den Wertebereich natürlich anpassen. Da hier der Exponent eine Definitionslücke bei x=0 hat, ist auch $\mathbb{D}=\mathbb{R} \setminus \{0\}.$

e hoch 1 durch x quadrat, Exponentialfunktion, e hoch x — Abbildung einer verketteten Exponentialfunktion

Symmetrie

Der Graph der normalen Exponentialfunktion weist keinerlei Symmetrien auf, er ist weder achsensymmetrisch noch punktsymmetrisch!

Anders sieht die Sache wieder bei den komplizierteren Exponentialfunktionen aus. Im obigen Bild siehst du sofort, dass dieser Graph achsensymmetrisch zur y-Achse verläuft. In solchen Fällen musst du die Symmetrie explizit nachrechnen!

Achsensymmetrie: f(-x) = f(x)

Punktsymmetrie: f(-x) = -f(x) .

In obigem Beispiel ist $f(x)=e^{\frac{1}{x^2}$ achsensymmetrisch wegen

$f(-x)=e^{\frac{1}{-x^2}} = e^{\frac{1}{x^2}$ .

Monotonie

im Videozum Video springen

Die e-Funktion f(x)=e^x ist überall streng monoton steigend, das bedeutet für alle Werte x_1<x_2 ist immer auch f(x_1)<f(x_2) .

Für schwierigere Funktionen trifft dies aber nicht automatisch zu. So ist beispielsweise die Funktion

$f(x) = e^{-x^3+2x}$

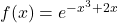
nicht überall streng monoton steigend. Wie du ihre Maxima und Minima berechnest, erklären wir dir im Artikel zu den Ableitungen .

Monotonie, e-Funktion Monotonie — Beispiel verkettete nicht-monotone Exponentialfunktion

Grenzverhalten

Für das Verhalten an den Rändern des Definitionsbereichs gilt:

$\lim\limits_{x\rightarrow \infty} e^x = \infty$

$\lim\limits_{x\rightarrow -\infty} e^x = 0$

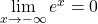
Damit ist die x-Achse eine waagrechte Asymptote von 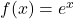f(x) = e^x .

Merke: Ist die Exponentialfunktion f(x)=e^x+d durch den Parameter nach oben oder nach unten verschoben, ändert dies natürlich auch die Asymptote!

Merke: Die Exponentialfunktion steigt schneller als jede Polynomfunktion. Ihr Verhalten dominiert bei der Grenzwertbetrachtung! Oft musst du hier aber die Regeln von l’Hospital zur Bestimmung des Grenzwertes verwenden.

Das gilt auch für das nächste Beispiel:

$\lim\limits_{x\rightarrow -\infty} e^x(x^2-2) = 0$

Grenzverhalten, Exponentialfunktion — Limes verketteter Exponentialfunktionen

Schnittpunkte mit den Achsen

Aufgrund des Grenzverhaltens und weil die x-Achse eine waagrechte Asymptote der e-Funktion ist, hat sie keine Nullstellen. Es gibt somit keinen Wert, für den e^x=0 erfüllt ist!

Dafür verläuft die e Funktion – wie alle Exponentialfunktionen der Form f(x) = b^x durch den Punkt (0|1) , was der einzige Schnittpunkt mit der y-Achse ist

e^0=1.

In obiger Grafik siehst du jedoch, dass beispielsweise die Funktion f(x)=e^x(x^2-2) Nullstellen bei x^2-2=0 hat. Den Schnittpunkt mit der y-Achse bei (-2|0) berechnest du auch hier, indem du x=0 einsetzt.

e-Funktion Rechenregeln

Wie bei allen Exponentialfunktionen gelten auch bei der e-Funktion bestimmte Rechenregeln, mit denen du die Terme gegebenenfalls vereinfachen kannst:

Rechenregeln für die Exponentialfunktion

$e^{x+y} = e^x \cdot e^y$

$e^{x-y} = \cfrac{e^x}{e^y}$

$e^{x \cdot y} = \left( e^x\right)^y$

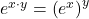
Umkehrfunktion der e Funktion

im Videozur Stelle im Video springen

Du weißt bereits, dass die Umkehrfunktion einer Exponentialfunktion die Logarithmus Funktion ist. Die Umkehrfunktion der e-Funktion ist somit auch eine Logarithmus-Funktion, sie wird als natürlicher Logarithmus oder als $\ln(x)$ bezeichnet.

Umkehrfunktion der e-Funktion:

$f^{-1}(x)=ln(x)$

Sprechweise: „l n x“

e hoch x, lnx, e Funktion, ln Funktion, e-Funktion, natürlicher logarithmus, umkehrfunktion — e-Funktion und ln-Funktion

Graphisch entspricht die Umkehrfunktion immer einer Spiegelung an der Winkelhalbierenden, weswegen du aus vielen Eigenschaften der natürlichen Exponentialfunktion direkt auf die ln Funktion schließen kannst.

Du brauchst die ln Funktion immer dann, wenn du eine Gleichung berechnen willst, die eine Exponentialfunktion enthält. Ein typisches Beispiel dafür ist die Berechnung der Nullstellen von $f(x) = e^{x^2-5x+4}-1$ :

$e^{x^2-5x+4}-1=0 \quad \quad \quad \quad \quad \bigg| +1$

$e^{x^2-5x+4}=1 \quad \quad \quad \quad \quad \bigg| \ln()$

$x^2-5x+4=\ln(1)=0$

$x_1=1 \quad x_2=4$

Ausführlich erklären wir dir die ln-Funktion aber in einem eigenen Video .

e Funktion ableiten

im Videozur Stelle im Video springen

Wie du die e Funktion ableiten kannst, erklären wir dir ebenfalls ausführlich in einem eigenen Video . Da die natürliche Exponentialfunktion die einzige Funktion ist, deren Steigung immer gleich ihrem Funktionswert ist, ist ihre Ableitung immer wieder die Funktion selbst.

Ableitung e Funktion

f'(x)= e^x

Für kompliziertere Ausdrücke benötigst du bei der Berechnung der Ableitung verschiedene Ableitungsregeln , wie beispielsweise hier die Kettenregel

$f(x)=e^{x^2-5x+4}-1$

$f'(x) = e^{x^2-5x+4} \cdot (2x-5)$ .

Integration der e Funktion

im Videozur Stelle im Video springen

Wenn die e Funktion ableiten so einfach ist, ist auch das uneigentliche Integral nicht schwer zu berechnen.

Stammfunktion e-Funktion

$\int e^x dx = e^x+c$

Für kompliziertere Ausdrücke kann es jedoch sein, dass du partiell integrieren oder substituieren musst.

e-Funktion zusammengefasst

Das Wichtigste zur e-Funktion siehst du hier:

Die e-Funktion hat die Gleichung f(x) = e^x (gesprochen: e hoch x). Ihre Basis ist die Eulersche Zahl e und ihr Exponent ist die Variable x. Die e-Funktion gehört zu den Exponentialfunktionen und wird auch natürliche Exponentialfunktion genannt.

Definitionsbereich : $\mathbb{D}=\mathbb{R}$

Wertebereich: $\mathbb{W}=\mathbb{R}^+$

Symmetrie: f(x)=e^x ist nicht symmetrisch

Monotonie: f(x)=e^x ist streng monoton steigend

Asymptote: f(x)=e^x hat eine waagrechte Asymptote bei x =0

y-Achsenabschnitt: 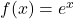f(x) = e^x verläuft immer durch den Punkt (0|1)

Umkehrfunktion: $f^{-1}(x)=\ln(x)$ , genannt ln Funktion

Ableitung: f'(x) = e^x

Stammfunktion: $F(x) = \int e^x dx = e^x+c$

Quiz zum Thema e Funktion

ln Funktion

Super! Nun weißt du alles Wichtige zur e Funktion. In einem weiteren Video erklären wir dir die ln Funktion und gehen noch einmal auf den Zusammenhang zwischen der e Funktion und der ln Funktion ein. Schau es dir unbedingt gleich an!

Zum Video: ln Funktion

zur Videoseite: e Funktion

Beliebte Inhalte aus dem Bereich Funktionen

Exponentialfunktion

E Funktion einfach erklärt

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .