Polynomdivision
Hier zeigen wir dir an einem ausführlichen Beispiel wie die Polynomdivision funktioniert. Mit unserem animierten Video verstehst du das Thema sofort.
Inhaltsübersicht
Polynomdivision einfach erklärt
Bei der Polynomdivision teilst du ein Polynom durch ein anderes. Polynome sind mehrgliedrige Terme, die Potenzen enthalten, wie diese hier:
f(x) = 5x2 + 3x – 12,
g(x) = x – 4.
Mit der Polynomdivision kannst du also zum Beispiel (5x2 + 3x – 12) : (x – 4) ausrechnen. Das funktioniert vom Prinzip her ähnlich wie das schriftliche Teilen in der Grundschule. In unserem Einsteiger-Artikel erklären wir dir das ausführlicher.
Wie genau du auf die unten stehende Lösung kommst, erklären wir dir gleich Schritt für Schritt.

Polynomdivision Schritt-für-Schritt Anleitung
Wir wollen nun  durch
durch  teilen:
teilen:
( 5x2 + 3x -12 ) : ( x – 4 ) = ?
Erster Durchgang
Schritt 1: Im ersten Schritt müssen wir uns überlegen, womit wir  multiplizieren müssen, um
multiplizieren müssen, um  zu erhalten. Die Antwort
zu erhalten. Die Antwort  schreiben wir als ersten Teil der Lösung rechts neben das
schreiben wir als ersten Teil der Lösung rechts neben das  -Zeichen.
-Zeichen.
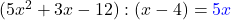
Schritt 2: Als nächstes multiplizieren wir die gefundenen  mit dem Divisor
mit dem Divisor  . Das Ergebnis
. Das Ergebnis  schreiben wir unter das erste Polynom. Wie bei der schriftlichen Division müssen wir davor aber noch ein Minus-Zeichen und einen Strich darunter setzen.
schreiben wir unter das erste Polynom. Wie bei der schriftlichen Division müssen wir davor aber noch ein Minus-Zeichen und einen Strich darunter setzen.

Schritt 3: Jetzt ziehen wir  vom Polynom darüber ab und schreiben das Ergebnis unter den Strich. Du siehst, das funktioniert wieder genauso wie beim schriftlichen Teilen normaler Zahlen.
vom Polynom darüber ab und schreiben das Ergebnis unter den Strich. Du siehst, das funktioniert wieder genauso wie beim schriftlichen Teilen normaler Zahlen.

Zweiter Durchgang
Schritt 4: Mit dem ersten Durchgang sind wir fertig. Die Schritte 1 bis 3 wiederholen wir anschließend mit dem Term, der noch übrig ist:  . Wir fragen uns wieder womit man
. Wir fragen uns wieder womit man  multiplizieren muss, um
multiplizieren muss, um  zu erhalten. Die Antwort
zu erhalten. Die Antwort  schreiben wir wieder auf die Ergebnisseite rechts:
schreiben wir wieder auf die Ergebnisseite rechts:

Schritt 5: Die  multiplizieren wir anschließend mit
multiplizieren wir anschließend mit  und schreiben das Ergebnis unter das Restpolynom. Zum Schluss setzen wir noch ein Minuszeichen davor und ziehen einen Strich darunter.
und schreiben das Ergebnis unter das Restpolynom. Zum Schluss setzen wir noch ein Minuszeichen davor und ziehen einen Strich darunter.

Schritt 6: Wieder ziehen wir nun die  vom Restpolynom ab und schreiben das Ergebnis 80 unter den Strich.
vom Restpolynom ab und schreiben das Ergebnis 80 unter den Strich.

Dritter Durchgang
Schritt 7: Auch den zweiten Durchgang haben wir damit geschafft. Wenn wir uns jetzt überlegen, womit wir  multiplizieren müssen, um auf
multiplizieren müssen, um auf  zu kommen, dann sehen wir, dass das nicht geht. Wir sind also fast am Ende der Polynomdivision angekommen. Wir müssen nur noch den Rest zum Ergebnis schreiben. Dafür schreiben wir einfach
zu kommen, dann sehen wir, dass das nicht geht. Wir sind also fast am Ende der Polynomdivision angekommen. Wir müssen nur noch den Rest zum Ergebnis schreiben. Dafür schreiben wir einfach  zur Lösung.
zur Lösung.

Übrigens, wir haben einen extra Beitrag mit Polynomdivision Aufgaben ! Dort erklären wir dir noch viele weitere Beispiele Schritt für Schritt.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Nullstellen finden mit der Polynomdivision
Musst du für ein Polynom dritten Grades die Nullstellen berechnen und kennst bereits eine Nullstelle, dann kannst du mit der Polynomdivision einfach die weiteren Nullstellen finden: Du teilst das Polynom einfach durch x Minus die gefundene Nullstelle. Das Ergebnis wird dann ein Polynom zweiten Grades sein für das du dann mit der Mitternachtsformel oder der abc-Formel die Nullstellen bestimmen kannst.
Aufgabe 1: Polynomdivision ohne Rest
Bestimme das Ergebnis der Division des Polynoms  durch das Polynom
durch das Polynom  .
.
Lösung Aufgabe 1
Der Term mit dem höchsten Exponenten von  ist
ist  . Wir müssen daher
. Wir müssen daher  im ersten Schritt mit
im ersten Schritt mit  multiplizieren. Das Ergebnis dieser Multiplikation ist das Polynom
multiplizieren. Das Ergebnis dieser Multiplikation ist das Polynom  . Dieses ziehen wir nun von
. Dieses ziehen wir nun von  ab und erhalten als Ergebnis
ab und erhalten als Ergebnis  .
.
Das Polynom  besitzt als Term mit dem höchsten Exponenten
besitzt als Term mit dem höchsten Exponenten  . Somit müssen wir
. Somit müssen wir  diesmal mit 4 multiplizieren und erhalten als Ergebnis
diesmal mit 4 multiplizieren und erhalten als Ergebnis  . Subtrahieren wir jetzt diese beiden Polynome
. Subtrahieren wir jetzt diese beiden Polynome  und
und  voneinander, erhalten wir als Ergebnis Null. Damit ist die Polynomdivision zu Ende. Das Gesamtergebnis sieht dann so aus:
voneinander, erhalten wir als Ergebnis Null. Damit ist die Polynomdivision zu Ende. Das Gesamtergebnis sieht dann so aus:

Aufgabe 2: Polynomdivision mit Rest
Du hast folgende Polynome gegeben
 und
und
 .
.
Bestimme das Ergebnis der Division von  durch
durch  .
.
Lösung Aufgabe 2
Das Polynom  besitzt als Term mit höchsten Exponent den Ausdruck
besitzt als Term mit höchsten Exponent den Ausdruck  . Wir müssen daher
. Wir müssen daher  mit
mit  multiplizieren und erhalten als Ergebnis das Polynom
multiplizieren und erhalten als Ergebnis das Polynom  . Dieses ziehen wir von
. Dieses ziehen wir von  ab und bekommen
ab und bekommen  (in der Polynomdivision wird immer nur der Term mit dem nächstgrößeren Exponenten verwendet; hier also nur
(in der Polynomdivision wird immer nur der Term mit dem nächstgrößeren Exponenten verwendet; hier also nur  ).
).
Um  zu eliminieren, müssen wir
zu eliminieren, müssen wir  mit
mit  multiplizieren. Das Ergebnis dieser Multiplikation ist
multiplizieren. Das Ergebnis dieser Multiplikation ist  und die Subtraktion der beiden Polynome
und die Subtraktion der beiden Polynome  und
und  führt zu
führt zu  (jetzt wird der Term mit dem nächstgrößeren Exponenten (hier die 9) zu diesem Polynom ergänzt).
(jetzt wird der Term mit dem nächstgrößeren Exponenten (hier die 9) zu diesem Polynom ergänzt).
Jetzt multiplizieren wir  mit 13 und ziehen das Ergebnis von
mit 13 und ziehen das Ergebnis von  ab. Wir erhalten daraus die Zahl 35, welche einen Exponenten von Null besitzt. Der höchste Exponent von
ab. Wir erhalten daraus die Zahl 35, welche einen Exponenten von Null besitzt. Der höchste Exponent von  ist aber 1 und damit ist die Polynomdivision zu Ende. Das Gesamtergebnis sieht dann so aus.
ist aber 1 und damit ist die Polynomdivision zu Ende. Das Gesamtergebnis sieht dann so aus.

Noch mehr Aufgaben zur Polynomdivision zeigen wir dir Schritt für Schritt in einem extra Video!
