Video anzeigen

Strahlensätze

Wichtige Inhalte in diesem Video

Strahlensätze einfach erklärt

1. Strahlensatz

Beispiel 1. Strahlensatz

2. Strahlensatz

Beispiel 2. Strahlensatz

Du willst wissen, was die Strahlensätze sind und wofür du sie brauchst? Hier und in unserem Video erfährst du es!

Inhaltsübersicht

Strahlensätze einfach erklärt

im Videozur Stelle im Video springen

(00:11)

Mit den Strahlensätzen kannst du die unbekannte Länge bestimmter Strecken bestimmen, wie zum Beispiel die Höhe eines Turms oder die Breite eines Flusses!

Dafür brauchst du:

zwei Strahlen bzw. Geraden, die sich in einem Zentrum Z treffen.
zwei Parallelen, die die Geraden schneiden. Die Parallelen können entweder auf der gleichen Seite des Schnittpunkts Z liegen oder auf zwei verschiedenen Seiten.

Strahlensätze, Strahlensätze Voraussetzungen, Strahlensätze Parallelen und Geraden, Strahlensatz, Zentrum, Parallel, Geradenn, A, B, Z — Strahlensätze

Sind diese Voraussetzungen erfüllt, kannst du verschiedene Streckenverhältnisse aufstellen. Du unterscheidest diese Verhältnisgleichungen:

1. Strahlensatz: Der erste Strahlensatz vergleicht nur die Abschnitte auf den beiden Strahlen.

$\frac{\textcolor{red}{\overline{ZA}}}{\textcolor{blue}{\overline{ZB}}} = \frac{\textcolor{orange}{\overline{ZA'}}}{\textcolor{purple}{\overline{ZB'}}}$

2. Strahlensatz: Der zweite Strahlensatz setzt Abschnitte auf den Parallelen ins Verhältnis zu den Abschnitten auf einem Strahl.

$\frac{\textcolor{olive}{\overline{AB}}}{\textcolor{red}{\overline{ZA}}} = \frac{\textcolor{olive}{\overline{A'B'}}}{\textcolor{orange}{\overline{ZA'}}}$

1. Strahlensatz

im Videozur Stelle im Video springen

(00:56)

Betrachte die zwei Strahlen, die sich im Punkt Z kreuzen. Der erste Strahlensatz beschreibt das Verhältnis zwischen den kurzen und langen Streckenabschnitten auf den zwei Strahlen.

1. Strahlensatz, Strahlensatz, Strahlensätze — 1. Strahlensatz

Für die Streckenverhältnisse gilt dann

$\frac{\textcolor{red}{\overline{ZA}}}{\textcolor{blue}{\overline{ZB}}} = \frac{\textcolor{orange}{\overline{ZA'}}}{\textcolor{purple}{\overline{ZB'}}}$ (1. Strahlensatz).

Auf der linken Seite werden also die Teilabschnitte des unteren Strahls ins Verhältnis gesetzt. Auf der rechten Seite der Gleichung die Teilabschnitte des oberen Strahls. Je nachdem, welche Strecken gegeben sind und welche Strecke gesucht ist, kannst du die Gleichung wie gewohnt umformen. Schauen wir es uns an!

Beispiel 1. Strahlensatz

im Videozur Stelle im Video springen

(01:23)

Gegeben: $\textcolor{red}{\overline{ZA} = 5\text{cm}}, \textcolor{blue}{\overline{ZB} = 3\text{cm}}, \textcolor{purple}{\overline{ZB'} = 7\text{cm}}$

Gesucht: $\textcolor{orange}{\overline{ZA'}}$

Die gesuchte Strecke kannst du mit Hilfe der Strahlensätze berechnen.

Verhältnisgleichung aufstellen

$\frac{\textcolor{red}{\overline{ZA}}}{\textcolor{blue}{\overline{ZB}}} = \frac{\textcolor{orange}{\overline{ZA'}}}{\textcolor{purple}{\overline{ZB'}}}$

Nach gesuchter Größe umstellen

$\frac{\textcolor{red}{\overline{ZA}}}{\textcolor{blue}{\overline{ZB}}} = \frac{\textcolor{orange}{\overline{ZA'}}}{\textcolor{purple}{\overline{ZB'}}} \quad \quad \big\vert \cdot \textcolor{purple}{\overline{ZB'}}$

$\textcolor{orange}{\overline{ZA'}}= \frac{\textcolor{red}{\overline{ZA}}}{\textcolor{blue}{\overline{ZB}}} \cdot \textcolor{purple}{\overline{ZB'}}$

Angaben einsetzen

$\textcolor{orange}{\overline{ZA'}}= \frac{\textcolor{red}{5\text{cm}}}{\textcolor{blue}{3\text{cm}}} \cdot \textcolor{purple}{7\text{cm}}$

Ergebnis berechnen

$\textcolor{orange}{\overline{ZA'}} = \frac{35}{3}\text{cm} \approx 11,7\text{cm}$

2. Strahlensatz

im Videozur Stelle im Video springen

(02:24)

Der 2. Strahlensatz setzt die Streckenabschnitte auf den Parallelen zu den Streckenabschnitten auf einem Strahl ins Verhältnis. Dabei können beide Strahlen zum Vergleich herangezogen werden. Manchmal werden die Parallelen auch als Geraden dargestellt, das heißt die Linien enden nicht an den Strahlen, sondern werden darüber hinaus verlängert. Solange die beiden Geraden aber weiterhin parallel sind, gilt der Strahlensatz weiterhin.

Zweiter Strahlensatz, Strahlensatz, 2 strahlensatz — Zweiter Strahlensatz

Mit der bekannten Schreibweise sieht das wie folgt aus.

$\frac{\textcolor{red}{\overline{AB}}}{\textcolor{blue}{\overline{ZA}}} = \frac{\textcolor{orange}{\overline{A'B'}}}{\textcolor{purple}{\overline{ZA'}}}$ (2. Strahlensatz)

Es ist auch möglich, den anderen Strahl als Vergleichsmaß zu nutzen.

$\frac{\textcolor{red}{\overline{AB}}}{\overline{ZB}} = \frac{\textcolor{orange}{\overline{A'B'}}}{\overline{ZB'}}$

Bei verschiedenen Aufgaben wählst du entsprechend den Strahl aus, für den du die Angaben besser nutzen kannst. Wichtig ist nur, dass du dich auf beiden Seiten der Gleichung auf denselben Strahl beziehst.

Beispiel 2. Strahlensatz

im Videozur Stelle im Video springen

(02:51)

Gegeben: $\textcolor{blue}{\overline{ZA} = 2\text{cm}}, \textcolor{orange}{\overline{A'B'} = 4\text{cm}}, \textcolor{purple}{\overline{ZA'} = 6\text{cm}}$

Gesucht: $\textcolor{red}{\overline{AB}}$

Die gesuchte Strecke kannst du mit dem zweiten Strahlensatz berechnen.

Verhältnisgleichung aufstellen

$\frac{\textcolor{red}{\overline{AB}}}{\textcolor{blue}{\overline{ZA}}} = \frac{\textcolor{orange}{\overline{A'B'}}}{\textcolor{purple}{\overline{ZA'}}}$

Nach gesuchter Größe umstellen

$\frac{\textcolor{red}{\overline{AB}}}{\textcolor{blue}{\overline{ZA}}} = \frac{\textcolor{orange}{\overline{A'B'}}}{\textcolor{purple}{\overline{ZA'}}} \quad \quad \big\vert \cdot \textcolor{blue}{\overline{ZA}}$

$\textcolor{red}{\overline{AB}}= \frac{\textcolor{orange}{\overline{A'B'}}}{\textcolor{purple}{\overline{ZA'}}} \cdot \textcolor{blue}{\overline{ZA}}$

Angaben einsetzen

$\textcolor{red}{\overline{AB}} = \frac{\textcolor{orange}{4\text{cm}}}{\textcolor{purple}{6\text{cm}}} \cdot \textcolor{blue}{2\text{cm}}$

Ergebnis berechnen

$\textcolor{red}{\overline{AB}} = \frac{4}{3}\text{cm} \approx 1,33 \text{cm}$

Strahlensatz Aufgaben

Sehen wir uns gleich noch einige Strahlensatz Aufgaben zum Üben an. Dabei gehst du immer gleich vor:

Verhältnisgleichung aufstellen
Nach gesuchter Größe umstellen
Angaben einsetzen
Ergebnis berechnen

Legen wir los!

Strahlensatz Aufgabe 1

Berechne die Länge der Strecke x.

Strahlensatz Aufgabe, Strahlensatz Aufgaben, Strahlensätze Aufgaben — Strahlensatz Aufgabe 1

Lösung Aufgabe 1

Zuerst musst du überlegen, welchen der Strahlensätze du anwenden kannst. Hier bietet sich der zweite Strahlensatz an.

Verhältnisgleichung aufstellen

$\frac{\overline{AB}}{\overline{ZA}} = \frac{x}{\overline{ZA'}}$

Nach gesuchter Größe umstellen

$\frac{\overline{AB}}{\overline{ZA}} = \frac{x}{\overline{ZA'}} \quad \quad \big \vert \cdot \overline{ZA'}$

$x = \frac{\overline{AB}}{\overline{ZA}} \cdot \overline{ZA'}$

Angaben einsetzen

Achtung, hier musst du zunächst die gesamte Streckenlänge $\overline{ZA'}$ berechnen.

$\overline{ZA'} = 10\text{m} + 5\text{m} = 15\text{m}$

Nun kannst du wie gewohnt die Angaben einsetzen.

$x = \frac{4\text{m}}{10\text{m}} \cdot 15\text{m}$

Ergebnis berechnen

$x = 6\text{m}$

Die gesuchte Strecke x ist also 6m lang.

Strahlensatz Aufgabe 2

Bestimme die Streckenlänge x.

Lösung Aufgabe 2

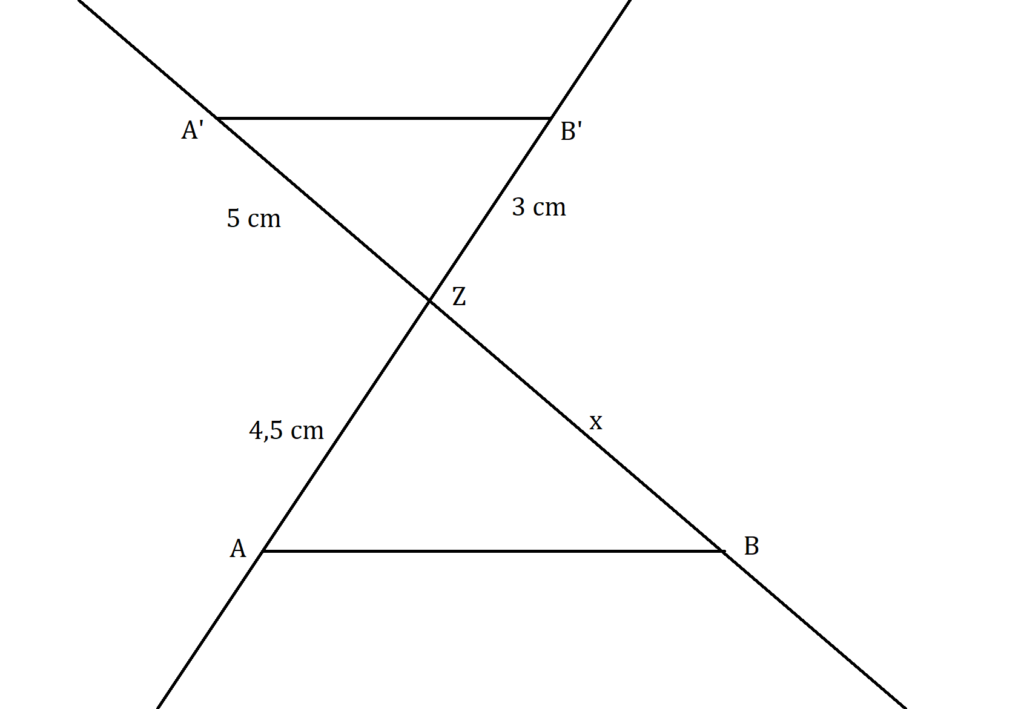
Auch hier brauchst du zur Lösung einen der Strahlensätze, diesmal den ersten. Lass dich nicht davon irritieren, dass die beiden parallelen Strecken in diesem Beispiel auf unterschiedlichen Seiten des Schnittpunkts Z liegen. Die Strahlensätze gelten trotzdem.

Verhältnisgleichung aufstellen

$\frac{\overline{ZA}}{\overline{x}} = \frac{\overline{ZA'}}{\overline{ZB'}}$

Nach gesuchter Größe umstellen

Diesmal steht die gesuchte Größe im Nenner. Deshalb notierst du dir lieber ein paar Umformungen mehr.

$\begin{align*} \frac{\overline{ZA}}{\overline{x}} &= \frac{\overline{ZA'}}{\overline{ZB'}} && | \cdot x \\ \overline{ZA} &= \frac{\overline{ZA'}}{\overline{ZB'}} \cdot x && | \cdot \frac{\overline{ZB'}}{\overline{ZA'}} \\ \overline{ZA} \cdot \frac{\overline{ZB'}}{\overline{ZA'}} &= x \\ x &= \overline{ZA} \cdot \frac{\overline{ZB'}}{\overline{ZA'}} \end{align*}$

Angaben einsetzen

$x = 4,5\text{cm} \cdot \frac{3\text{cm}}{5\text{cm}}$

Ergebnis berechnen

$x = \frac{27}{10}\text{cm} = 2,7 \text{cm}$

Strahlensatz Anwendung

Wie wir dir oben schon angekündigt haben, kannst du die Strahlensätze bei einer ganzen Reihe von Anwendungsaufgaben verwenden. Immer, wenn du die Länge von Streckenabschnitten suchst, solltest du deshalb Ausschau nach zwei Strahlen und Parallelen halten. Gehen wir mal zusammen eine Anwendungsaufgabe durch.

Du stehst 18 Meter von einem Turm entfernt und wir nehmen einmal an, dass du 1,70m groß bist. Wie hoch ist der Turm?

Strahlensatz Aufgabe 3, Strahlensatz Aufgaben, Strahlensätze Aufgaben — Strahlensatz Aufgabe 3

Auch dieses Problem kannst du mit den Strahlensätzen lösen. Dabei bildest du als Mensch eine Parallele zum Turm, so wie in der Skizze eingezeichnet. Der eine Strahl verläuft auf dem Boden und der andere verbindet deinen Kopf mit der Spitze des Turms.

Gegeben: $\overline{ZA} = 2\text{m}, \overline{AB} = 1,7\text{m}, \overline{AA'} = 18\text{m}$

Gesucht: h

Verhältnisgleichung aufstellen

Weil du hier eine der parallelen Strecken suchst, brauchst du den zweiten Strahlensatz.

$\frac{\overline{AB}}{\overline{ZA}} = \frac{h}{\overline{ZA'}}$

Nach gesuchter Größe umstellen

$h = \frac{\overline{AB}}{\overline{ZA}} \cdot \overline{ZA'}$

Angaben einsetzen

Auch in diesem Beispiel musst du zunächst die gesamte Streckenlänge $\overline{ZA'}$ berechnen.

$\overline{ZA'} = 2\text{m} + 18\text{m} = 20\text{m}$

Nun kannst du wieder die Angaben einsetzen.

$h = \frac{1,7\text{m}}{2\text{m}} \cdot 20\text{m}$

Ergebnis berechnen

$h = 17\text{m}$

Der Turm ist genau 17 Meter hoch.

Winkel berechnen

Weißt kannst du mit den Strahlensätze Strecken berechnen. Manchmal musst du aber auch Winkel bestimmen . Wie das geht, erfährst du in unserem Video!

Geometrie

Rechteck und Quadrat

Geometrie

Vierecke

Geometrie

Dreiecke Grundlagen

Geometrie

Dreiecke Sätze

Geometrie

Geometrische Grundlagen

Geometrie

Symmetrie

Geometrie

Kreis berechnen

Geometrie

Kreis

Geometrie

Geometrische Körper

Geometrie

Abstandsrechnung

Geometrie

Ebenen

Geometrie

Differentialgeometrie

Strahlensätze

Strahlensätze einfach erklärt