Gradmaß und Bogenmaß berechnen
Du musst einen Winkel von Grad in Bogenmaß oder von Bogenmaß in Grad umrechnen? Wir zeigen dir, wie das geht! Lehn dich zurück und schau einfach schnell unser Video .
Inhaltsübersicht
Gradmaß und Bogenmaß einfach erklärt
Gradmaß und Bogenmaß sind Winkelmaße, mit denen du die Größe eines Winkels darstellen kannst. Ein Winkel hat immer einen Wert im Bogenmaß und im Gradmaß. In der Grafik ist  der Winkel im Gradmaß und
der Winkel im Gradmaß und  ist derselbe Winkel im Bogenmaß.
ist derselbe Winkel im Bogenmaß.
Du siehst, dass  und
und  den gleichen Winkel beschreiben. Es gibt also einen Weg zur Umrechnung von Grad in Bogenmaß und umgekehrt. Die beiden Formeln für Grad in Bogenmaß bzw. Bogenmaß in Grad sehen wir folgt aus.
den gleichen Winkel beschreiben. Es gibt also einen Weg zur Umrechnung von Grad in Bogenmaß und umgekehrt. Die beiden Formeln für Grad in Bogenmaß bzw. Bogenmaß in Grad sehen wir folgt aus.
Einen Winkel kannst du mit der folgenden Formel vom Gradmaß ins Bogenmaß umrechnen.

Du kannst natürlich auch in die andere Richtung eine Umrechnung von Bogenmaß zu Grad durchführen.

Legen wir direkt mit Beispielen zur Umrechnung los.
Grad in Bogenmaß
Mithilfe der oberen Formel ist die Umrechnung eines Winkels von Grad in Bogemaß für dich kein Problem mehr.

Jetzt zeigen wir dir die Anwendung mit zwei Beispielen.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Beispiel
Forme  vom Gradmaß ins Bogenmaß um.
vom Gradmaß ins Bogenmaß um.
- 1. Formel aufstellen: Schreibe die Formel für die Umrechnung von Grad in Bogenmaß auf.

-
2. Gradmaß einsetzen: Setze den Wert
 in die Bogenmaß Formel ein.
in die Bogenmaß Formel ein.

- 3. Bogenmaß berechnen: Rechne das Grad zu Bogenmaß um.

Für einen Winkel mit 60° im Gradmaß kannst du das Bogenmaß berechnen und bekommst einen Winkel im Bogenmaß von ungefähr 1,047.
Bogenmaß in Grad
Mit der Bogenmaß Formel kannst du auch ganz leicht die Berechnung Bogenmaß zu Gradmaß durchführen.

Schau dir einfach das folgende Beispiel an, damit das Rechnen für dich wirklich kein Problem mehr ist.
Beispiel
Angenommen du sollst einen Winkel  vom Bogenmaß ins Gradmaß umrechnen, dann gehst du wie folgt vor:
vom Bogenmaß ins Gradmaß umrechnen, dann gehst du wie folgt vor:
- 1. Formel aufstellen: Schreibe die Formel für das Winkel umrechnen von Bogenmaß zu Grad auf.

-
2. Bogenmaß einsetzen: Setze den Winkel im Bogenmaß
 in die Gradmaß Formel ein.
in die Gradmaß Formel ein.

- 3. Gradmaß berechnen: Zuletzt musst du noch das Ergebnis berechnen.

Du siehst, dass ein Bogenmaß Winkel mit Wert 1 einem Winkel in Grad von ungefähr 57,3° entspricht.
Bogenmaß Tabelle
In der Tabelle siehst du auf einen Blick ein paar wichtige Werte von Grad in Bogenmaß umgerechnet.
Gradmaß 
|
Umrechnung | Bogenmaß 
|
| 0° |  |
 |
| 30° |  |
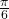 |
| 90° |  |
 |
| 180° |  |
 |
| 360° |  |
 |
Kommen wir als letztes noch zur Herleitung der beiden Formeln.
Bogenmaß berechnen
Anhand des linken Kreises siehst du, dass ein kompletter Innenwinkel im Gradmaß 360° entspricht. Das heißt, dass ein Winkel  im Gradmaß einen Anteil am Innenwinkel hat von
im Gradmaß einen Anteil am Innenwinkel hat von  .
.
Beim rechten Kreis kannst du erkennen, dass der Innenwinkel im Bogenmaß  entspricht. Daraus kannst du schließen, dass ein Winkel
entspricht. Daraus kannst du schließen, dass ein Winkel  im Bogenmaß einen Innenwinkel-Anteil von
im Bogenmaß einen Innenwinkel-Anteil von  hat.
hat.
Willst du das Gradmaß mit dem Bogenmaß vergleichen, musst du beide Verhältnisse gleichsetzen.
 =
= 
Für die Umrechnung von Grad in Bogenmaß hast du  gegeben und suchst
gegeben und suchst  . Du findest
. Du findest  , indem du danach auflöst.
, indem du danach auflöst.
 =
= 

Beim Umrechnen von Bogenmaß zu Grad hast du  gegeben und suchst
gegeben und suchst  . Löse die Gleichung nach
. Löse die Gleichung nach  auf.
auf.
 =
= 

Du kannst in beiden Gleichungen noch 360° mit 2 kürzen.


So bekommst du die Formeln für die Umrechnung Grad in Bogenmaß bzw. Bogenmaß in Grad, die du schon am Anfang gesehen hast. Ein Winkel im Bogenmaß hat eine Einheit, die man Radiant (rad) schreibt, aber meistens weglässt.
Einheitskreis und Bogenmaß
Du musst auch wissen, dass das Bogenmaß an einem Kreis mit einem Radius gleich eins definiert ist; so einen Kreis mit r = 1 nennt man auch Einheitskreis. Am Einheitskreis kann man natürlich mehr als nur das Bogenmaß definieren, also schau dir für den richtigen Durchblick unbedingt unser Video zum Einheitskreis an!




