Video
Quiz

Teste dein Wissen zum Thema Sinus Cosinus Tangens!

sin cos tan Tabelle

Übersicht sin cos tan Tabelle

Du suchst sin, cos und tan Tabellen und fragst dich: Was sind die Sinus, Kosinus und Tangens Werte von bestimmten Winkeln im Grad- oder Bogenmaß? In den folgenden Winkeltabellen findest du die passenden Werte auf einen Blick!

Quiz zum Thema Sinus Cosinus Tangens
5 Fragen beantworten
Inhaltsübersicht

sin cos tan Tabelle

Die folgenden drei Winkeltabellen zeigen dir jeweils die Werte von Sinus, Cosinus und Tangens in Schritten von 15° (bzw. π /12).

Sinus Tabelle

Winkel α im Gradmaß Winkel α im Bogenmaß sin(α) exakt sin(α) gerundet
0° (360°) 0 (2π) 0  0,0000
15° (-345°) 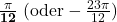\mathbf{\frac{\pi}{12}} \; (\text{oder}-\frac{23\pi}{12}) \frac{\sqrt{6}-\sqrt{2}}{4} 0,2588
30° (-330°) \mathbf{\frac{\pi}{6}}\; (\text{oder}-\frac{11\pi}{6}) \frac{1}{2} 0,5000
45° (-315°) \mathbf{\frac{\pi}{4}}\; (\text{oder}-\frac{7\pi}{4}) \frac{\sqrt{2}}{2} 0,7071
60° (-300°) \mathbf{\frac{\pi}{3}}\; (\text{oder}-\frac{5\pi}{3}) \frac{\sqrt{3}}{2} 0,8660
75° (-285°) \mathbf{\frac{5\pi}{12}} \; (\text{oder}-\frac{19\pi}{12}) \frac{\sqrt{6}+\sqrt{2}}{4} 0,9659
90° (-270°) \textcolor{red}{\mathbf{\frac{\pi}{2}}\; (\text{oder}-\frac{3\pi}{2})} 1 1,0000
105°(-255°) \mathbf{\frac{7\pi}{12}}\; (\text{oder}-\frac{17\pi}{12}) \frac{\sqrt{6}+\sqrt{2}}{4} 0,9659
120° (-240°) \mathbf{\frac{2\pi}{3}} \; (\text{oder}-\frac{4\pi}{3}) \frac{\sqrt{3}}{2} 0,8660
135° (-225°) \mathbf{\frac{3\pi}{4}} \; (\text{oder}-\frac{5\pi}{4}) \frac{\sqrt{2}}{2} 0,7071
150° (-210°) \mathbf{\frac{5\pi}{6}}\; (\text{oder}-\frac{7\pi}{6}) \frac{1}{2} 0,5000
165° (-195°) \mathbf{\frac{11\pi}{12}}\; (\text{oder}-\frac{13\pi}{12}) \frac{\sqrt{6}-\sqrt{2}}{4} 0,2588
180° (-180°) \textcolor{red}{\mathbf{\pi}\; (\text{oder}-\pi)} 0 0,0000
195° (-165°) \mathbf{\frac{13\pi}{12}} \; (\text{oder}-\frac{11\pi}{12}) \frac{-\sqrt{6}+\sqrt{2}}{4} -0,2588
210° (-150°) \mathbf{\frac{7\pi}{6}} \; (\text{oder}-\frac{5\pi}{6}) -\frac{1}{2} -0,5000
225° (-135°) \mathbf{\frac{5\pi}{4}}\; (\text{oder}-\frac{3\pi}{4}) -\frac{\sqrt{2}}{2} -0,7071
240° (-120°) \mathbf{\frac{4\pi}{3}}\; (\text{oder}-\frac{2\pi}{3}) -\frac{\sqrt{3}}{2} -0,8660
255° (-105°) \mathbf{\frac{17\pi}{12}}\; (\text{oder}-\frac{7\pi}{12}) \frac{-\sqrt{6}-\sqrt{2}}{4} -0,9659
270° (-90°) \textcolor{red}{\mathbf{\frac{3\pi}{2}} \; (\text{oder}-\frac{\pi}{2})} -1 -1,0000
285° (-75°) \mathbf{\frac{19\pi}{12}} \; (\text{oder}-\frac{5\pi}{12}) \frac{-\sqrt{6}-\sqrt{2}}{4} -0,9659
300° (-60°) \mathbf{\frac{5\pi}{3}}\; (\text{oder}-\frac{\pi}{3}) -\frac{\sqrt{3}}{2} -0,8660
315° (-45°) \mathbf{\frac{7\pi}{4}} \; (\text{oder}-\frac{\pi}{4}) -\frac{\sqrt{2}}{2} -0,7071
330° (-30°) \mathbf{\frac{11\pi}{6}}\; (\text{oder}-\frac{\pi}{6}) -\frac{1}{2} -0,5000
345° (-15°) \mathbf{\frac{23\pi}{6}} \; (\text{oder}-\frac{\pi}{12}) \frac{-\sqrt{6}+\sqrt{2}}{4} -0,2588
Negative Winkel in Sinus, Cosinus oder Tangens Tabellen

Manchmal hast du auch negative Winkel im Grad- oder Bogenmaß gegeben. Da Sinus, Cosinus und Tangens sich aber nach 360° (bzw. 2π) wiederholen, kannst du einfach den Winkel plus 360° rechnen und hast dann einen positiven Winkel. Den Sinus, Cosinus oder Tangens Wert davon kannst du dann in der entsprechenden Tabelle nachschauen.

Beispiel: sin(-345°) = sin(15°)

Cosinus Tabelle

Winkel α im Gradmaß Winkel α im Bogenmaß cos(α) exakt cos(α) gerundet
0° (360°) 0 (2π) 1 1,0000
15° (-345°) \mathbf{\frac{\pi}{12}}\; (\text{oder}-\frac{23\pi}{12}) \frac{\sqrt{6}+\sqrt{2}}{4} 0,9659
30° (-330°) \mathbf{\frac{\pi}{6}}\; (\text{oder}-\frac{11\pi}{6}) \frac{\sqrt{3}}{2} 0,8660
45° (-315°) \mathbf{\frac{\pi}{4}}\; (\text{oder}-\frac{7\pi}{4}) \frac{\sqrt{2}}{2} 0,7071
60° (-300°) \mathbf{\frac{\pi}{3}}\; (\text{oder}-\frac{5\pi}{3}) \frac{1}{2} 0,5000
75° (-285°) \mathbf{\frac{5\pi}{12}} \; (\text{oder}-\frac{19\pi}{12}) \frac{\sqrt{6}-\sqrt{2}}{4} 0,2588
90° (-270°) \textcolor{red}{\mathbf{\frac{\pi}{2}} \; (\text{oder}-\frac{3\pi}{2})} 0 0,0000
105° (-255°) \mathbf{\frac{7\pi}{12}} \; (\text{oder}-\frac{17\pi}{12}) \frac{-\sqrt{6}+\sqrt{2}}{4} -0,2588
120° (-240°) \mathbf{\frac{2\pi}{3}} \; (\text{oder}-\frac{4\pi}{3}) -\frac{1}{2} -0,5000
135° (-225°) \mathbf{\frac{3\pi}{4}} \; (\text{oder}-\frac{5\pi}{4}) -\frac{\sqrt{2}}{2} -0,7071
150° (-210°) \mathbf{\frac{5\pi}{6}}\; (\text{oder}-\frac{7\pi}{6}) -\frac{\sqrt{3}}{2} -0,8660
165° (-195°) \mathbf{\frac{11\pi}{12}} \; (\text{oder}-\frac{13\pi}{12}) \frac{-\sqrt{6}-\sqrt{2}}{4} -0,9659
180° (-180°) \textcolor{red}{\mathbf{\pi}\; (\text{oder}-\pi)} -1 -1,0000
195° (-165°) \mathbf{\frac{13\pi}{12}}\; (\text{oder}-\frac{11\pi}{12}) \frac{-\sqrt{6}-\sqrt{2}}{4} -0,9659
210° (-150°) \mathbf{\frac{7\pi}{6}} \; (\text{oder}-\frac{5\pi}{6}) -\frac{\sqrt{3}}{2} -0,8660
225° (-135°) \mathbf{\frac{5\pi}{4}} \; (\text{oder}-\frac{3\pi}{4}) -\frac{\sqrt{2}}{2} -0,7071
240° (-120°) \mathbf{\frac{4\pi}{3}}\; (\text{oder}-\frac{2\pi}{3}) -\frac{1}{2} -0,5000
255° (-105°) \mathbf{\frac{17\pi}{12}}\; (\text{oder}-\frac{7\pi}{12}) \frac{-\sqrt{6}+\sqrt{2}}{4} -0,2588
270° (-90°) \textcolor{red}{\mathbf{\frac{3\pi}{2}}\; (\text{oder}-\frac{\pi}{2})} 0 0,0000
285° (-75°) \mathbf{\frac{19\pi}{12}} \; (\text{oder}-\frac{5\pi}{12}) \frac{\sqrt{6}-\sqrt{2}}{4} 0,2588
300° (-60°) \mathbf{\frac{5\pi}{3}}\; (\text{oder}-\frac{\pi}{3}) \frac{1}{2} 0,5000
315° (-45°) \mathbf{\frac{7\pi}{4}} \; (\text{oder}-\frac{\pi}{4}) \frac{\sqrt{2}}{2} 0,7071
330° (-30°) \mathbf{\frac{11\pi}{6}}\; (\text{oder}-\frac{\pi}{6}) \frac{\sqrt{3}}{2} 0,8660
345° (-15°) \mathbf{\frac{23\pi}{6}} \; (\text{oder}-\frac{\pi}{12}) \frac{\sqrt{6}+\sqrt{2}}{4} 0,9659
Zusammenhang Sinustabelle und Kosinustabelle

Wenn du die Sinus Werte aus der Tabelle hast, kennst du damit auch schon die Kosinus Werte! Es sind nämlich dieselben, nur um 90° (bzw. π/2) verschoben. Also cos(α) = sin(α+90°).

Beispiel: cos(180°) = sin(270°) = -1

Tangens Tabelle

Winkel α im Gradmaß Winkel α im Bogenmaß tan(α) exakt tan(α) gerundet
0° (360°) 0 (2π) 0 0,0000
15° (-345°) 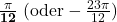\mathbf{\frac{\pi}{12}} \; (\text{oder}-\frac{23\pi}{12}) 2-\sqrt{3} 0,2679
30° (-330°) \mathbf{\frac{\pi}{6}}\; (\text{oder}-\frac{11\pi}{6}) \frac{\sqrt{3}}{3} 0,5774
45° (-315°) \mathbf{\frac{\pi}{4}} \;(\text{oder}-\frac{7\pi}{4}) 1 1,0000
60° (-300°) \mathbf{\frac{\pi}{3}} \;(\text{oder}-\frac{5\pi}{3}) \sqrt{3} 1,7321
75° (-285°) \mathbf{\frac{5\pi}{12}} \;(\text{oder}-\frac{19\pi}{12}) 2+\sqrt{3} 3,7321
90° (-270°) \textcolor{red}{\mathbf{\frac{\pi}{2}}\; (\text{oder}-\frac{3\pi}{2})} \textcolor{red}{\to \infty} –
105° (-255°) \mathbf{\frac{7\pi}{12}}\; (\text{oder}-\frac{17\pi}{12}) -2-\sqrt{3} -3,7321
120° (-240°) \mathbf{\frac{2\pi}{3}}\; (\text{oder}-\frac{4\pi}{3}) -\sqrt{3} -1,7321
135° (-225°) \mathbf{\frac{3\pi}{4}}\; (\text{oder}-\frac{5\pi}{4}) -1 -1,0000
150° (-210°) \mathbf{\frac{5\pi}{6}}\; (\text{oder}-\frac{7\pi}{6}) -\frac{\sqrt{3}}{3} -0,5774
165° (-195°) \mathbf{\frac{11\pi}{12}}\; (\text{oder}-\frac{13\pi}{12}) -2+\sqrt{3} -0,2679
180° (-180°) \textcolor{red}{\mathbf{\pi}\; (\text{oder}-\pi)} 0 0,0000
195° (-165°) \mathbf{\frac{13\pi}{12}} \;(\text{oder}-\frac{11\pi}{12}) 2-\sqrt{3} 0,2679
210° (-150°) \mathbf{\frac{7\pi}{6}}\; (\text{oder}-\frac{5\pi}{6}) \frac{\sqrt{3}}{3} 0,5774
225° (-135°) \mathbf{\frac{5\pi}{4}} \; (\text{oder}-\frac{3\pi}{4}) 1 1,0000
240° (-120°) \mathbf{\frac{4\pi}{3}} (\text{oder}-\frac{2\pi}{3}) \sqrt{3} 1,7321
255° (-105°) \mathbf{\frac{17\pi}{12}} \; (\text{oder}-\frac{7\pi}{12}) 2+\sqrt{3} 3,7321
270° (-90°) \textcolor{red}{\mathbf{\frac{3\pi}{2}}\; (\text{oder}-\frac{\pi}{2})} \textcolor{red}{\to -\infty} –
285° (-75°) \mathbf{\frac{19\pi}{12}}\; (\text{oder}-\frac{5\pi}{12}) -2-\sqrt{3} -3,7321
300° (-60°) \mathbf{\frac{5\pi}{3}}\; (\text{oder}-\frac{\pi}{3}) -\sqrt{3} -1,7321
315° (-45°) \mathbf{\frac{7\pi}{4}} \; (\text{oder}-\frac{\pi}{4}) -1 -1,0000
330° (-30°) \mathbf{\frac{11\pi}{6}}\; (\text{oder}-\frac{\pi}{6}) -\frac{\sqrt{3}}{3} -0,5774
345° (-15°) \mathbf{\frac{23\pi}{6}}\; (\text{oder}-\frac{\pi}{12}) -2+\sqrt{3} -0,2679

Tipp: Mit den Sinus und Cosinus Werten kannst du auch die Winkeltabelle für den Tangens ausfüllen. Es gilt nämlich: tan(α) = sin(α)/cos(α).

Quiz zum Thema Sinus Cosinus Tangens
5 Fragen beantworten

Winkelfunktionen

In diesen Bogenmaß- und Gradmaß Tabellen kannst du nun ganz einfach die Werte für Sinus, Kosinus und Tangens ablesen. Du willst wissen, was du noch alles mit den Winkelfunktionen machen kannst? Dann schau dir gleich unser Video dazu an!

Winkelfunktionen
Zum Video: Winkelfunktionen
  zur Videoseite: Sinus Cosinus Tangens

Beliebte Inhalte aus dem Bereich Funktionen

  zur Videoseite: Sinus Cosinus Tangens

Weitere Inhalte: Funktionen

Trigonometrie
Trigonometrie
Dauer: 04:00
Sinus
Dauer: 04:26
Cosinus
Dauer: 04:25
Tangens
Dauer: 04:41
Sinus Cosinus Tangens
Dauer: 03:57
Periodizität
Dauer: 04:20

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .