Video

Quiz

Hier geht's zum Video „Wurzeln addieren und subtrahieren“

Wurzeln multiplizieren und dividieren

Wichtige Inhalte in diesem Video

Wurzeln multiplizieren – einfach erklärt

Gleichnamige Wurzeln multiplizieren

Ungleichnamige Wurzeln multiplizieren

Gleichnamige Wurzeln dividieren

Ungleichnamige Wurzeln dividieren

Du fragst dich, wie du Wurzeln multiplizierst und dividierst? Hier und im Video erklären wir dir, wie das funktioniert und worauf genau du achten musst!

Inhaltsübersicht

Wurzeln multiplizieren – einfach erklärt

im Videozur Stelle im Video springen

Um Wurzeln zu multiplizieren, gibt es eine einfache Grundregel: Du multiplizierst die Zahlen unter den Wurzeln (Radikanden) miteinander und ziehst anschließend die Wurzel aus dem Ergebnis.

Beispiel

$\sqrt{\textcolor{red}4} \cdot \sqrt{\textcolor{red}9}$

Multipliziere die Radikanden:
$\textcolor{red}4 \cdot \textcolor{red}9 = \textcolor{blue}{36}$
Ziehe die Wurzel aus dem Ergebnis:
$\sqrt{\textcolor{blue}{36}}=6$

Das bedeutet, das Ergebnis ist:

$\sqrt{4} \cdot \sqrt{9} = 6$

Gleichnamige Wurzeln multiplizieren

im Videozur Stelle im Video springen

Gleichnamige Wurzeln sind Wurzeln, mit denselben Wurzelexponenten. Zum Beispiel haben $\sqrt[\textcolor{olive}2]{\textcolor{red}4}$ und $\sqrt[\textcolor{olive}2]{\textcolor{red}9}$ beide eine 2 im Exponenten. Daher sind sie gleichnamig.

Um gleichnamige Wurzeln zu multiplizieren, folge diesen Schritten:

Stelle sicher, dass die Wurzeln gleichnamig sind.
Multipliziere die Radikanden.
Ziehe die Wurzel aus dem Produkt.

Beispiel:

$\sqrt[\textcolor{olive}{2}]{\textcolor{red}2} \text{ und } \sqrt[\textcolor{olive}{2}]{\textcolor{red}8}$

Beides sind Quadratwurzeln. Also sind die Wurzeln gleichnamig.
Multipliziere die Radikanden: $\textcolor{red}2 \cdot \textcolor{red}8 = \textcolor{blue}{16}$
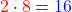
Ziehe die Wurzel aus dem Produkt: $\sqrt[\textcolor{olive}{2}]{\textcolor{red}{16}} = 4$

Das Ergebnis ist 4.

Ungleichnamige Wurzeln multiplizieren

im Videozur Stelle im Video springen

Ungleichnamige Wurzeln haben verschiedene Wurzelexponenten, zum Beispiel eine 2 und eine 3. Bevor du sie multiplizieren kannst, musst du sie auf eine gemeinsame Wurzel bringen. Das machst du mit den folgenden Schritten:

Finde einen gemeinsamen Wurzelexponenten.
Schreibe die Wurzeln mit dem gemeinsamen Exponenten um.
Multipliziere die Radikanden.
Ziehe die gemeinsame Wurzel aus dem Produkt.

Beispiel:

$\sqrt[\textcolor{olive}2]{\textcolor{red}5}\cdot\sqrt[\textcolor{olive}3]{\textcolor{red}9}$

Finde den gemeinsamen Exponenten. Dafür musst du die Exponenten der Wurzeln multiplizieren: $\textcolor{olive}2 \cdot \textcolor{olive}3 = 6$
Schreibe die Wurzeln um. Dafür erweiterst du die Wurzel auf den neuen Exponenten 6.
$\begin{align*} \sqrt[\textcolor{olive}{2}]{\textcolor{red}{5}} = \sqrt[\textcolor{olive}{6}]{\textcolor{red}{5^{\textcolor{olive}{3}}}} = \sqrt[\textcolor{olive}{6}]{\textcolor{red}{125}} \\ \sqrt[\textcolor{olive}{3}]{\textcolor{red}{9}} = \sqrt[\textcolor{olive}{6}]{\textcolor{red}{9^{\textcolor{olive}{2}}}} = \sqrt[\textcolor{olive}{6}]{\textcolor{red}{81}} \end{align*}$
Multipliziere die Radikanden: $\textcolor{red}{125} \cdot \textcolor{red}{81} = \textcolor{blue}{10125}$
Ziehe die Wurzel aus dem Ergebnis: $\sqrt[\textcolor{olive}6]{\textcolor{blue}{10125}}$

Das Endergebnis ist $\sqrt[6]{10125}$ .

Wurzeln dividieren — einfach erklärt

Um Wurzeln zu dividieren, benutzt du eine ähnliche Grundregel wie bei der Multiplikation: Du dividierst die Radikanden und ziehst anschließend die Wurzel aus dem Ergebnis.

Beispiel:

$\sqrt{\textcolor{red}{25}} \div \sqrt{\textcolor{red}{5}}$

Dividiere die Radikanden: $\textcolor{red}{25} \div \textcolor{red}{5} = \textcolor{blue}{5}$
Ziehe die Wurzel aus dem Ergebnis: $\sqrt{\textcolor{blue}{5}}$

Da du $\sqrt{5}$ nicht mehr vereinfachen kannst, ist das Ergebnis $\sqrt{25} \div \sqrt{5} = \sqrt{5}$ .

Gleichnamige Wurzeln dividieren

im Videozur Stelle im Video springen

Gleichnamige Wurzeln haben wieder den gleichen Wurzelexponenten. Du dividierst sie mit den folgenden Schritten:

Stelle sicher, dass die Wurzeln gleichnamig sind.
Dividiere die Radikanden.
Ziehe die Wurzel aus dem Ergebnis.

Beispiel:

$\sqrt[\textcolor{olive}2]{\textcolor{red}{8}}\div\sqrt[\textcolor{olive}2]{\textcolor{red}2}$

Die Wurzeln sind beides Quadratwurzeln. Also sind sie gleichnamig.
Dividiere die Radikanden $\textcolor{red}{8}\div\textcolor{red}{2}=\textcolor{blue}{4}$
Ziehe die Wurzel aus dem Ergebnis: $\sqrt[\textcolor{olive}{2}]{\textcolor{blue}{4}}=2$

Ungleichnamige Wurzeln dividieren

im Videozur Stelle im Video springen

Ungleichnamige Wurzeln haben verschiedene Wurzelexponenten. Auch beim Dividieren musst du sie erst und müssen auf eine gemeinsame Wurzel bringen. Das machst du so:

Finde einen gemeinsamen Wurzelexponenten.
Schreibe die Wurzeln mit dem gemeinsamen Exponenten um.
Dividiere die Radikanden.
Ziehe die gemeinsame Wurzel aus dem Ergebnis.

Beispiel:

$\sqrt[\textcolor{olive}{3}]{\textcolor{red}{27}}\div \sqrt[\textcolor{olive}{2}]{\textcolor{red}{3}}$

Finde den gemeinsamen Exponenten, indem du die Exponenten der Wurzeln multiplizierst: $\textcolor{olive}{3} \cdot\textcolor{olive}{2} = 6$
Schreibe die Wurzeln um:
$\begin{align*} \sqrt[\textcolor{olive}{3}]{\textcolor{red}{27}} = \sqrt[\textcolor{olive}{6}]{\textcolor{red}{27}^{\textcolor{olive}{2}}} = \sqrt[\textcolor{olive}{6}]{\textcolor{red}{729}} \\ \sqrt[\textcolor{olive}{2}]{\textcolor{red}{3}} = \sqrt[\textcolor{olive}{6}]{\textcolor{red}{3}^{\textcolor{olive}{3}}} = \sqrt[\textcolor{olive}{6}]{\textcolor{red}{27}} \end{align*}$
Dividiere die Radikanden: $\textcolor{red}{729} \div \textcolor{red}{27} = \textcolor{blue}{27}$
Ziehe die Wurzel aus dem Ergebnis: $\sqrt[\textcolor{olive}{6}]{\textcolor{blue}{27}}$

Das Endergebnis ist $\sqrt[6]{27}$ .

Wurzeln multiplizieren und dividieren — häufigste Fragen

Was mache ich, wenn die Wurzeln unterschiedliche Exponenten haben?
Du musst die Wurzeln gleichnamig machen. Multipliziere die Exponenten der Wurzeln, um einen gemeinsamen Exponenten zu finden. Schreibe die Wurzeln mit diesem Exponenten um. Beispiel: $\sqrt[2]{3}$ und $\sqrt[3]{9}$ werden beide zur sechsten Wurzel: $\sqrt[6]{27}$ und $\sqrt[6]{81}$ , bevor du sie multiplizierst oder dividierst.
Warum muss ich Wurzeln gleichnamig machen?
Nur gleichnamige Wurzeln lassen sich korrekt multiplizieren oder dividieren. Unterschiedliche Wurzelexponenten verhindern eine direkte Verrechnung der Radikanden. Gleichnamig machen stellt sicher, dass die Radikanden korrekt kombiniert werden können.

Wurzeln addieren und subtrahieren

Schau dir unser weiteres Video auf unserer Seite an, um zu erfahren, wie du Wurzeln addierst und subtrahierst.

Zum Video: Wurzeln addieren und subtrahieren

Beliebte Inhalte aus dem Bereich Mathematische Grundlagen

Wurzeln addieren und subtrahieren

Wurzeln multiplizieren und dividieren

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .