Punkt vor Strich
In diesem Beitrag zeigen wir Dir was es mit der Punkt-vor-Strich-Regel auf sich hat und wie die Klammerrechnung funktioniert. Keine Lust, zu lesen? Dann schau dir einfach unser Video dazu an!
Inhaltsübersicht
Was ist die Punkt-vor-Strich-Regel? — einfach erklärt
Du fragst dich: Wie rechnet man Punkt-vor-Strich? Die Punkt-vor-Strich-Regel besagt, dass du immer erst Multiplikation ( • ) und Division ( : ) rechnen musst, bevor du Addition ( + ) und Subtraktion ( – ) angehst.
Es gilt immer: Punktrechnung geht vor Strichrechnung!
Die Punkt-vor-Strichrechnung hilft dir, deine Aufgaben immer in der richtigen Reihenfolge auszurechnen. Häufig ist das sehr wichtig, um die richtige Lösung zu finden.
Punkt-vor-Strich richtig anwenden — so geht’s!
Die Punkt-vor-Strichrechnung ist besonders wichtig, wenn die Aufgaben schwieriger werden. Folgendes Beispiel zeigt dir, warum du auf Punkt-vor-Strich achten musst:
Beispiel: Wie komme ich auf  ?
?
- Als erstes multiplizierst du:
 .
.
- Als zweites addierst du:
 .
.
- Vergisst du die Punkt-vor-Strich-Regel, erhältst du auch ein falsches Ergebnis!
Wenn du dir noch unsicher bist, schau dir unser Video und die Beispiele im nächsten Abschnitt an!
Addition (Plus-Zeichen) und Subtraktion (Minus-Zeichen) heißen Strichrechnung.
Multiplikation (Mal-Zeichen) und Division (Geteilt-Zeichen) heißen Punktrechnung.
Es gilt immer: Punktrechnung geht vor Strichrechnung!
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Beispiele für Punkt-vor-Strich
Du musst Strichrechnung (Addition, Subtraktion) und Punktrechnung (Multiplikation, Division) auseinander halten. Fange immer mit den Punktrechnungen an und rechne sie von links nach rechts aus. Danach kümmerst du dich um alle Strichrechnungen und rechnest auch diese von links nach rechts aus. Wie gesagt: Punkt- vor Strichrechnung! Probiere es gleich mit diesen Beispielen aus:
Beispiel 1: Hier rechnest du zuerst die Multiplikation und dann die Addition.
Beispiel 2: In diesem Beispiel fängst du mit der Division an und subtrahierst danach die 2.
Beispiel 3: Fange mit der Division an und mache mit der Multiplikation weiter. Zum Schluss subtrahierst du die 4 von der 6.
Beispiel 4: Hier multiplizierst und dividierst du zuerst. Ganz zum Schluss addierst du.
Die ersten drei Aufgaben ähneln unseren bisherigen Beispielen. In die letzten beiden Aufgaben haben wir zwei Multiplikationen. Diese Aufgaben kannst du aber wie die restlichen mit der Punkt-vor-Strich-Regel lösen: Rechne zuerst alle Multiplikationen (mal) und Divisionen (geteilt) nacheinander aus und danach die Additionen (plus) und Subtraktionen (minus).
So rechnest du mit Klammer-vor-Punkt-vor-Strich
Punkt- vor Strichrechnung hast du jetzt verstanden. Aber was machst du, wenn du zuerst addieren und danach teilen willst? Dafür gibt es die Klammerrechnung. Du schreibst das, was du zuerst berechnen möchtest zwischen Klammern. Du kannst deine Regel also so erweitern: Klammer vor Punkt vor Stich.
Beispiel: Warum ist  ?
?
- Zuerst rechnest du die Klammer aus:
 .
.
- Nachdem die Klammer ausgerechnet ist, machst du normal weiter:
 .
.
- Ohne Klammern würdest du so rechnen:
 .
.
In der Klammer benutzt du wie gewohnt deine Punkt-vor-Strich-Regel. Halte dich an folgenden Reihenfolge:
-
Zuerst rechnest Du Klammern aus.
-
Danach rechnest Du Multiplikation (mal) und Division (geteilt) aus.
-
Zuletzt kommt die Addition (plus) und Subtraktion (minus) dran.
Diese Beispiele helfen dir die Klammerrechnung zu verstehen:
Beispiel 1: Beginne mit der Klammer und multipliziere danach.
Beispiel 2: Beginne wieder in der Klammer und halte dich an die Punkt-vor-Strich-Regel.
Beipiel 3: Zuerst rechnest du die Klammer aus. Kümmer dich um die Addition zuletzt!
Beispiel 4: Denk daran: Klammer vor Punkt vor Strich!
Klammerrechnung mit mehreren Klammern
Wenn du über eine Aufgabe mit vielen Klammern stolpern solltest, lass dich nicht aus der Ruhe bringen! Halte dich einfach an Klammer-vor-Punkt-vor-Strich und arbeite dich von innen nach außen. Folgendes Beispiel zeigt dir, wie es geht.
Beispiel: Warum ist  ?
?
- Du fängst mit der innersten Klammer an und rechnest
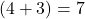 .
.
- Danach kümmerst du dich um die nächste Klammer:
![Rendered by QuickLaTeX.com [7 \cdot 2 -4] = [14 - 4] = 10](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-dddfb4e80e7c8a3945896c96336401d9_l3.png) .
.
- Zuletzt rechnest du
 .
.
- Egal wie viele Klammern es gibt, rechne eine nach der anderen von innen nach außen! Häufig siehst du auch eckige [ ] oder geschweifte Klammern { }. Die dienen nur der Lesbarkeit; behandele sie wie normale Klammern auch.
Rechne Klammern immer zuerst aus. Fange bei der innersten Klammer an und arbeite Dich von innen nach außen!
Schau dir am Besten diese Beispiele und unser Video an, damit Deine nächste Schulaufgabe läuft!
Einfache Aufgaben für Punkt- vor Strichrechnung
Damit bei deiner Schulaufgabe alles klappt, haben wir dir ein paar Übungsaufgaben zusammengestellt.
![Rendered by QuickLaTeX.com \[ \begin{array}{r ccc l} \textbf{Aufgabe:} & 5 &+& 2 \cdot 3 &= \;? \\[1ex] \textbf{Lösung:} & 5 &+& 2 \cdot 3 &= \\ & 5 &+& 6 &= 11 \\[2ex] % \textbf{Aufgabe:} & 20 & - &20 : 5 &= \; ? \\[1ex] \textbf{Lösung:} & 20 &-& 20 : 5 &= \\ & 20 &-& 4 &= 16 \\[2ex] % \textbf{Aufgabe:} & 14 : 2 &-& 2 \cdot 3 &= \;? \\[1ex] \textbf{Lösung:} & 14 : 2 &-& 2 \cdot 3 &= \\ & 7 &-& 2 \cdot 3 &= \\ & 7 &-& 6 &= 1 \\[2ex] % \textbf{Aufgabe:} & 2 \cdot 4 &+& 18 : 9 &= \; ? \\[1ex] \textbf{Lösung:} & 2 \cdot 4 &+& 18 : 9 &= \\ & 8 &+& 18 : 9 &= \\ & 8 & +& 2 &= 10 \end{array} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-a0b1058dc0fbbe469a7615dc915a6eca_l3.png)
Fortgeschrittene Aufgaben für Punkt- vor Strichrechnung
Da du jetzt die Punkt-vor-Strichrechnung auf dem Kasten hast, kannst du dich auch mal an etwas schwierigeren Aufgaben versuchen!
![Rendered by QuickLaTeX.com \[ \begin{array}{r ccccc l} \textbf{Aufgabe:}& \multicolumn{6}{l}{12 - 5 \cdot 4 : 2 =\;?} \\[1.5ex] \textbf{Hinweis:}& \multicolumn{6}{l}{ \text{Fange mit der Multiplikation an.} } \\[1.5ex] \textbf{Lösung:}& 12 &-& 5 \cdot 4 &:& 2 &= \\ & 12 &-& 20 &:& 2 &= \\ & 12 &-& & 10 & &= 2 \\[3ex] % \textbf{Aufgabe:}& \multicolumn{6}{l}{3 \cdot 3 - 9 : 3 \cdot 2 =\;?} \\[1.5ex] \textbf{Hinweis:} & \multicolumn{6}{l} {\text{Rechne Punkt vor Strich und von links nach rechts!} } \\[1.5ex] \textbf{Lösung:}& 3 \cdot 3 & - & 9 : 3 &\cdot & 2 &= \\ & 9 & - & 9 : 3 &\cdot & 2 &= \\ & 9 & - & 3 & \cdot & 2 &= \\ & 9 & - && 6 &&= 3 \\[3ex] % \textbf{Aufgabe:}& \multicolumn{6}{l}{13 \cdot ( 7 - 5 ) = \;?} \\[1.5ex] \textbf{Hinweis:}& \multicolumn{6}{l}{ \text{Klammer vor Punkt vor Strich!} } \\[1.5ex] \textbf{Lösung:}& 13 &\cdot& ( 7 - 5 ) &= \phantom{26} \\ &13 &\cdot& 2 &= 26 \\[3ex] % \textbf{Aufgabe:}& \multicolumn{6}{l}{ (16 - 4) : 3 \cdot 5 =\; ? } \\[1.5ex] \textbf{Hinweis:}& \multicolumn{6}{l}{ \text{Rechne von links nach rechts!} } \\[1.5ex] \textbf{Lösung:}& (16-4) &:& 3 &\cdot & 5 &= \\ & 12 &:& 3 &\cdot & 5 &= \\ & & 4 & & \cdot & 5 &= 20 \end{array} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-16a1a580138c783995eaf21388e31e83_l3.png)
Schwere Aufgaben für Punkt- vor Strichrechnung
Wenn du dich sicher fühlst, haben wir dir auch ein paar schwere Aufgaben vorbereitet.
![Rendered by QuickLaTeX.com \[ \begin{array}{r ccccccc l} \textbf{Aufgabe:}& \multicolumn{8}{l}{ ( 2 + 7) : (8-5) = \;? } \\[1.5ex] \textbf{Hinweis:}& \multicolumn{8}{l}{ \text{Rechne zuerst die Klammern eine nach der anderen aus.} } \\[1.5ex] \textbf{Lösung:}& ( 2 + 7) &:& (8-5) &= \phantom{3} \\ & 9 &:& (8-5) &= \phantom{3} \\ & 9 &:& 3 &= 3 \\[3ex] % \textbf{Aufgabe:}& \multicolumn{8}{l}{ (21 - 7) : (11 - 4) \cdot (3 + 8) = \;? } \\[1.5ex] \textbf{Hinweis:}& \multicolumn{8}{l}{ \text{Es gilt: Klammer vor Punkt vor Strich!} } \\[1.5ex] \textbf{Lösung:}& (21 - 7) &:& (11 - 4) &\cdot & (3 + 8) &= \phantom{22} \\ & 14 &:& 7 &\cdot & 11 &= \phantom{22} \\ & & 2 & &\cdot & 11 &= 22\\[3ex] % \textbf{Aufgabe:}& \multicolumn{8}{l}{ ( 2 \cdot (3 + 5) - 4 ) : 4 = \; ? } \\[1.5ex] \textbf{Hinweis:}& \multicolumn{8}{l}{ \text{Rechne Deine Klammern von innen nach außen.} } \\[1.5ex] \textbf{Lösung:}& ( 2 &\cdot& (3 + 5)& -& 4 )& :& 4 &= \\ & ( 2 &\cdot& 8 & -& 4 )& :& 4 &= \\ & &( 16 & & -& 4 )& :& 4 &= \\ & & & & 12 & & :& 4 &= 3 \\[3ex] % \textbf{Aufgabe:} & \multicolumn{8}{l}{ (2 + 3) \cdot [ 21 : (7-4) -4 ] = \; ? } \\[1.5ex] \textbf{Hinweis:}& \multicolumn{8}{l}{ \text{Alle Klammern nacheinander und von innen nach außen!} } \\[1.5ex] \textbf{Lösung:}& (2 + 3) & \cdot & [ 21 &:& (7-4)& -&4 ] &= \\ & 5 & \cdot & [ 21 &:& (7-4)& -&4 ] &= \\ & 5 & \cdot & [ 21 &:& 3 & -&4 ] &= \\ & 5 & \cdot & &[ 7& & -&4 ] &= \\ & 5 & \cdot & & & & 3 & &= 15 \end{array} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-5d2f62ba0a8cbca73a2ff3573be2719e_l3.png)
Terme vereinfachen
Die Punkt-vor-Strich-Regel brauchst du beispielsweise immer, wenn du Terme vereinfachen möchtest. Schau dir deshalb auch unbedingt noch unser Video dazu an – dann klappt auch sicher alles in der nächsten Prüfung!



















