Video anzeigen

Hier geht's zum Video „Negative Potenzen“

Potenzgesetze Wurzel

Wichtige Inhalte in diesem Video

Potenzgesetze Wurzel einfach erklärt

Wurzel multiplizieren

Wurzel dividieren

Wurzel in einer Wurzel

Du möchtest wissen, welche Potenzgesetze es für Wurzeln gibt und wie du sie anwendest? Hier im Beitrag und im Video findest du alles, was du dazu wissen musst!

Inhaltsübersicht

Potenzgesetze Wurzel einfach erklärt

im Videozur Stelle im Video springen

Wenn du Potenzgesetze bei Wurzeltermen anwenden möchtest, solltest du dir erst anschauen, wie eine Wurzel als Potenz dargestellt wird:

$\sqrt[n]{a} = a^{\frac{1}{n}}$

Anders als bei normalen Potenzen, setzt du bei Wurzeltermen für den Exponenten keine ganze Zahl wie 1 oder 2 ein, sondern rationale Zahlen wie ½ oder ¼. Auch wenn die Exponenten dabei Brüche sind, kannst du beim Rechnen die Potenzgesetze benutzen:

1. Potenzen mit gleicher Basis multiplizieren oder dividieren:

aⁿ • a^m = a^n+m oder $\frac{\textcolor{blue}{a}^{n}}{\textcolor{blue}{a}^{m}}$ = a^n-m

2^1/4 • 2^2/4 = 2^1/4+2/4= 2^3/4

$\frac{\textcolor{blue}{2}^{3/4}}{\textcolor{blue}{2}^{1/4}}$ = 2^3/4-1/4= 2^2/4

2. Potenzen mit gleichem Exponenten multiplizieren oder dividieren:

aⁿ • bⁿ = (a • b)ⁿ oder $\frac{a^{\textcolor{red}{n}}}{b^{\textcolor{red}{n}}}$ = $(\frac{a}{b})^{\textcolor{red}{n}}$

2^1/2 • 3^1/2 = (2 • 3)^1/2

$\frac{2^{\textcolor{red}{\frac{1}{2}}}}{3^{\textcolor{red}{\frac{1}{2}}}}$ = $(\frac{2}{3})^{\textcolor{red}{\frac{1}{2}}}$

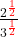3. Potenzen potenzieren:

(aⁿ)^m = aⁿ^•^m

(2^1/2)^4/5= 2^1/2^•^4/5

Wurzelgesetze

Das 2. und 3. Potenzgesetz kannst du allgemein auf Wurzeln übertragen. Dann gelten zusätzlich folgende Wurzelgesetze:

Die n-te Wurzel multiplizierst du, indem du die Radikanden multiplizierst:
$\sqrt[n]{a}\cdot\sqrt[n]{b} = \sqrt[n]{a\cdot b}$
Die n-te Wurzel dividierst du, indem du die Radikanden dividierst:
$\frac{\sqrt[n]{a}}{\sqrt[n]{b}} = \sqrt[n]{\frac{a}{b}}$
Die m-te Wurzel ziehst du aus einer n-ten Wurzel, indem du die Wurzelexponenten multiplizierst:
$\sqrt[m]{\sqrt[n]{a}} = \sqrt[m\cdot n]{a}$

Wurzel multiplizieren

im Videozur Stelle im Video springen

Mit den nächsten Beispielen zeigen wir dir, wie du von den Potenzgesetzen zu den Wurzelgesetzen kommst.

Beispiel: $\sqrt{\textcolor{red}{2}}\cdot\sqrt{\textcolor{red}{8}}$

Du kannst gleiche Wurzeln multiplizieren, indem du das 2. Potenzgesetz anwendest:

Schritt: Wandle die Wurzeln in Potenzen um:
$\sqrt{\textcolor{red}{2}}\cdot\sqrt{\textcolor{red}{8}} = \textcolor{red}{2}^{\frac{1}{2}}\cdot \textcolor{red}{8}^{\frac{1}{2}}$

Merke: Steht auf einer Wurzel keine Zahl $\sqrt{a}$ , kannst du dir eine 2 auf der Wurzel vorstellen $\sqrt[2]{a}$ . Du nennst sie auch Quadratwurzel. Die dazugehörige Potenz ist dann $a^{\frac{1}{2}}$ .
Schritt: Wende das 2. Potenzgesetz an:
$\textcolor{red}{2}^{\frac{1}{2}}\cdot \textcolor{red}{8}^{\frac{1}{2}} = (\textcolor{red}{2}\cdot \textcolor{red}{8})^{\frac{1}{2}} = \textcolor{red}{16}^{\frac{1}{2}}$
Schritt: Wandle die Potenz wieder in eine Wurzel um:
$\textcolor{red}{16}^{\frac{1}{2}} = \sqrt{\textcolor{red}{16}} = 4$

Du kommst schneller auf das gleiche Ergebnis, wenn du das 1. Wurzelgesetz anwendest: $\sqrt{\textcolor{red}{2}}\cdot\sqrt{\textcolor{red}{8}} = \sqrt{\textcolor{red}{2}\cdot \textcolor{red}{8}} = \sqrt{\textcolor{red}{16}} = 4$

1. Wurzelgesetz

Du kannst gleiche Wurzeln multiplizieren, indem du ihre Radikanden multiplizierst:

$\sqrt[n]{\textcolor{red}{a}}\cdot\sqrt[n]{\textcolor{red}{b}} = \sqrt[n]{\textcolor{red}{a}\cdot \textcolor{red}{b}}$

Wurzel dividieren

im Videozur Stelle im Video springen

Beispiel: $\frac{\sqrt[3]{\textcolor{red}{24}}}{\sqrt[3]{\textcolor{red}{3}}}$

Das Prinzip der Wurzeldivision ist gleich wie das der Wurzelmultiplikation. Du kannst gleiche Wurzeln dividieren, indem du das 2. Potenzgesetz anwendest:

Schritt: Wandle die Wurzeln in Potenzen um:
$\frac{\sqrt[3]{\textcolor{red}{24}}}{\sqrt[3]{\textcolor{red}{3}}} = \frac{\textcolor{red}{24}^{\frac{1}{3}}}{\textcolor{red}{3}^{\frac{1}{3}}}$
Schritt: Wende das 2. Potenzgesetz an:
$\frac{\textcolor{red}{24}^{\frac{1}{3}}}{\textcolor{red}{3}^{\frac{1}{3}}} = (\frac{\textcolor{red}{24}}{\textcolor{red}{3}})^{\frac{1}{3}} = \textcolor{red}{8}^{\frac{1}{3}}$
Schritt: Wandle die Potenz wieder in eine Wurzel um:
$\textcolor{red}{8}^{\frac{1}{3}} = \sqrt[3]{\textcolor{red}{8}} = 2$

Um auch hier schneller auf das Ergebnis zu kommen, wendest du das 2. Wurzelgesetz an: $\frac{\sqrt[3]{\textcolor{red}{24}}}{\sqrt[3]{\textcolor{red}{3}}} = \sqrt[3]{\frac{\textcolor{red}{24}}{\textcolor{red}{3}}} = \sqrt[3]{\textcolor{red}{8}} = 2$

2. Wurzelgesetz:

Du kannst gleiche Wurzeln dividieren, indem du ihre Radikanden dividierst:

$\frac{\sqrt[n]{\textcolor{red}{a}}}{\sqrt[n]{\textcolor{red}{b}}} = \sqrt[n]{\frac{\textcolor{red}{a}}{\textcolor{red}{b}}}$

Wurzel in einer Wurzel

im Videozur Stelle im Video springen

Beispiel: $\sqrt[\textcolor{orange}{3}]{\sqrt[\textcolor{orange}{4}]{5}}$

Wenn du eine Wurzel in einer Wurzel gegeben hast, dann kannst du für die Berechnung das 3. Potenzgesetz anwenden:

Schritt: Wandle die Wurzeln in Potenzen um:
$\sqrt[\textcolor{orange}{3}]{\sqrt[\textcolor{orange}{4}]{5}} = (5^{\frac{1}{\textcolor{orange}{4}}})^{\frac{1}{\textcolor{orange}{3}}}$
Schritt: Wende das 3. Potenzgesetz an:
$(5^{\frac{1}{\textcolor{orange}{4}}})^{\frac{1}{\textcolor{orange}{3}}} = 5^{\frac{1}{\textcolor{orange}{4}}}\cdot ^{\frac{1}{\textcolor{orange}{3}}} = 5^{\frac{1}{\textcolor{orange}{12}}}$
Schritt: Wandle die Potenz wieder in eine Wurzel um:
$5^{\frac{1}{\textcolor{orange}{12}}} = \sqrt[\textcolor{orange}{12}]{5} = 1,14$

Das 3. Wurzelgesetz erleichtert dir auch hier den Rechenweg: $\sqrt[\textcolor{orange}{3}]{\sqrt[\textcolor{orange}{4}]{5}} = \sqrt[\textcolor{orange}{3}\cdot \textcolor{orange}{4}]{5} = \sqrt[\textcolor{orange}{12}]{5} = 1,14$

3. Wurzelgesetz

Wenn du eine Wurzel in einer Wurzel gegeben hast, dann multiplizierst du die Wurzelexponenten:

$\sqrt[\textcolor{orange}{m}]{\sqrt[\textcolor{orange}{n}]{a}} = \sqrt[\textcolor{orange}{m\cdot n}]{a}$

Potenzgesetze Wurzel — häufigste Fragen

Was sind Potenzgesetze Wurzel?
Du kannst Potenzgesetze auch für Wurzeln anwenden. Dafür wandelst du die Wurzel in eine Potenz mit einem Bruch im Exponenten um. Nun kannst du mit den Potenzen weiterrechnen. Potenzgesetze werden in diesem Kontext oft auch Wurzelgesetze genannt.
Was bedeutet ein Bruch in einer Potenz?
Wenn du einen Bruch im Exponenten gegeben hast, dann ist das eine andere Darstellungsweise für eine Wurzel. Die Zahl, die im Nenner steht, ist der Grad deiner Wurzel und die Zahl, die im Zähler steht, ist die Hochzahl deines Radikanden.

Negative Potenzen

Jetzt weißt du, was es für Wurzelgesetze gibt und wie du sie anwendest. Du möchtest mehr über negative Potenzen erfahren? Dann schau in das Video rein!

Zum Video: Negative Potenzen

Beliebte Inhalte aus dem Bereich Mathematische Grundlagen

Potenzgesetze Wurzel

Potenzgesetze Aufgaben

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .