Video

Quiz

Hier geht's zum Video „Potenzgesetze“

Wurzelgesetze

Wichtige Inhalte in diesem Video

Wurzelgesetze einfach erklärt

Wurzelgesetz addieren

Wurzelgesetz subtrahieren

Wurzelgesetz multiplizieren

Wurzelgesetz dividieren

Wurzel als Potenz

Die Wurzelgesetze legen fest, wie du beim Rechnen mit Wurzeln vorgehst und was du beim Wurzelrechnen beachten musst. Schau dir unser Video an! Dort erklären wir dir die Wurzelregeln ausführlich mit vielen Beispielen.

Inhaltsübersicht

Wurzelgesetze einfach erklärt

im Videozur Stelle im Video springen

Die Wurzelgesetze brauchst du, um die Grundrechenarten (Plus, Minus, Mal, Geteilt) auf Wurzeln anwenden zu können. Schau dir dazu kurz an, wie eine Wurzel aufgebaut ist:

Sie besteht immer aus einem Wurzelzeichen, einem Wurzelexponenten und dem Radikand. Wenn der Wurzelexponent 2 ist, sprichst du von einer Quadratwurzel . Dann kannst du die 2 auch einfach weglassen. Ist der Exponent 3, hast du eine Kubikwurzel .

Wurzel, Wurzel Begriffe, Radikand, Wurzelexponent, Wurzelzeichen, Wurzel von x — Bezeichnungen einer Wurzel

Jetzt bist du bereit für die Wurzelregeln! Hier siehst du sie auf einen Blick:

Wurzelgesetz	Formel	Beispiel
Addition	$\textcolor{teal}{a}\sqrt[\textcolor{blue}{n}]{\textcolor{red}{x}} + \textcolor{teal}{b}\sqrt[\textcolor{blue}{n}]{\textcolor{red}{x}} = (\textcolor{teal}{a} + \textcolor{teal}{b}) \sqrt[\textcolor{blue}{n}]{\textcolor{red}{x}}$	$\textcolor{teal}{3}\sqrt{\textcolor{red}{2}} + \textcolor{teal}{5}\sqrt{\textcolor{red}{2}} = (\textcolor{teal}{3} + \textcolor{teal}{5}) \sqrt{\textcolor{red}{2}} = 8\sqrt{2}$
Subtraktion	$\textcolor{teal}{a}\sqrt[\textcolor{blue}{n}]{\textcolor{red}{x}} - \textcolor{teal}{b}\sqrt[\textcolor{blue}{n}]{\textcolor{red}{x}} = ( \textcolor{teal}{a} - \textcolor{teal}{b}) \sqrt[\textcolor{blue}{n}]{\textcolor{red}{x}}$	$\textcolor{teal}{5}\sqrt{\textcolor{red}{2}} - \textcolor{teal}{3}\sqrt{\textcolor{red}{2}} = ( \textcolor{teal}{5} - \textcolor{teal}{3}) \sqrt{\textcolor{red}{2}} = 2\sqrt{2}$
Multiplikation	$\sqrt[\textcolor{blue}{n}]{\textcolor{red}{x}} \cdot \sqrt[\textcolor{blue}{n}]{\textcolor{red}{y}} = \sqrt[\textcolor{blue}{n}]{\textcolor{red}{x\cdot y}}$	$\sqrt{\textcolor{red}{2}} \cdot \sqrt{\textcolor{red}{5}} = \sqrt{\textcolor{red}{2\cdot 5}} = \sqrt{10}$
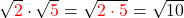Division	$\frac{\sqrt[\textcolor{blue}{n}]{\textcolor{red}{x}}}{\sqrt[\textcolor{blue}{n}]{\textcolor{red}{y}}} = \sqrt[\textcolor{blue}{n}]{\frac{\textcolor{red}{x}}{\textcolor{red}{y}}}$	$\frac{\sqrt{\textcolor{red}{10}}}{\sqrt{\textcolor{red}{5}}} = \sqrt{\frac{\textcolor{red}{10}}{\textcolor{red}{5}}} = \sqrt{2}$
Potenzieren	$(\sqrt[n]{x})^{\textcolor{blue}{m}} = \sqrt[n]{x^\textcolor{blue}{m}}$	$(\sqrt{2})^{\textcolor{blue}{3}} = \sqrt{2^\textcolor{blue}{3}}$
Radizieren	$\sqrt[\textcolor{blue}{m}]{\sqrt[\textcolor{blue}{n}]{\textcolor{red}{x}}} = \sqrt[\textcolor{blue}{m} \cdot \textcolor{blue}{n}]{\textcolor{red}{x}}$	$\sqrt[\textcolor{blue}{3}]{\sqrt[\textcolor{blue}{4}]{\textcolor{red}{2}}} = \sqrt[\textcolor{blue}{3} \cdot \textcolor{blue}{4}]{\textcolor{red}{2}} = \sqrt[12]{2}$

Das ging dir zu schnell? Dann schau dir jetzt die Wurzel Rechenregeln im Detail an!

Wurzelgesetz addieren

im Videozur Stelle im Video springen

Bei der Addition setzen die Wurzelregeln voraus, dass der Wert n auf der Wurzel (Wurzelexponent) und der Wert x unter der Wurzel (Radikand) gleich sind. Dazu addierst du die beiden Koeffizienten, also die Zahlen, die vor den Wurzeln stehen.

$\textcolor{teal}{a}\sqrt[\textcolor{blue}{n}]{\textcolor{red}{x}} + \textcolor{teal}{b}\sqrt[\textcolor{blue}{n}]{\textcolor{red}{x}} = (\textcolor{teal}{a} + \textcolor{teal}{b}) \sqrt[\textcolor{blue}{n}]{\textcolor{red}{x}}$

Beispiel

Du sollst folgende Wurzeln addieren

$\textcolor{teal}{5}\sqrt[\textcolor{blue}{3}]{\textcolor{red}{7}}+\textcolor{teal}{1}\sqrt[\textcolor{blue}{3}]{\textcolor{red}{7}}$ .

Da beide Summanden den gleichen Wurzelexponenten 3 und den Radikand 7 haben, kannst du die Wurzeln ganz einfach addieren, indem du die beiden Koeffizienten 5 und 1 zusammenzählst.

$(\textcolor{teal}{5} + \textcolor{teal}{1}) \sqrt[\textcolor{blue}{3}]{\textcolor{red}{7}} = \textcolor{teal}{6} \sqrt[\textcolor{blue}{3}]{\textcolor{red}{7}}$

Hinweis: Wenn vor der Wurzel x der Koeffizient 1 steht, wird er meist weggelassen. Zum Wurzeln addieren kannst du die 1 einfach wieder ergänzen.

$\sqrt[n]{x} = \textcolor{teal}{1}\cdot\sqrt[n]{x}$

Wurzelgesetz subtrahieren

im Videozur Stelle im Video springen

Das Wurzelgesetz zur Subtraktion funktioniert genauso wie bei der Addition, nur dass du anstelle von plus nun minus rechnest.

$\textcolor{teal}{a}\sqrt[\textcolor{blue}{n}]{\textcolor{red}{x}} - \textcolor{teal}{b}\sqrt[\textcolor{blue}{n}]{\textcolor{red}{x}} = (\textcolor{teal}{a} - \textcolor{teal}{b}) \sqrt[\textcolor{blue}{n}]{\textcolor{red}{x}}$

Beispiel

Subtrahiere die Wurzeln.

$\textcolor{teal}{7}\sqrt[\textcolor{blue}{4}]{\textcolor{red}{3}}-\textcolor{teal}{5}\sqrt[\textcolor{blue}{4}]{\textcolor{red}{3}}$

Beide Glieder haben unter der Wurzel die Zahl 3 und für n die Zahl 4. Du rechnest also einfach 7 minus 5 und ziehst es vor die Wurzel.

$(\textcolor{teal}{7}-\textcolor{teal}{5})\sqrt[\textcolor{blue}{4}]{\textcolor{red}{3}} = \textcolor{teal}{2}\sqrt[\textcolor{blue}{4}]{\textcolor{red}{3}}$

Wurzelgesetz multiplizieren

im Videozur Stelle im Video springen

Die Wurzelregeln bei der Multiplikation setzen voraus, dass Wurzeln den gleichen Exponenten n haben, damit du sie multiplizieren kannst. In dem Fall können die Radikanden einfach multipliziert werden, ohne dass sich das n ändert.

$\sqrt[\textcolor{blue}{n}]{\textcolor{red}{x}} \cdot \sqrt[\textcolor{blue}{n}]{\textcolor{red}{y}} = \sqrt[\textcolor{blue}{n}]{\textcolor{red}{x\cdot y}}$

Beispiel

Du sollst folgende Wurzeln mit den Wurzel Rechenregeln multiplizieren.

$\sqrt[\textcolor{blue}{3}]{\textcolor{red}{4}}\cdot\sqrt[\textcolor{blue}{3}]{\textcolor{red}{5}}$

Der Wert n ist bei beiden Wurzeln gleich 3. Du multiplizierst daher die Radikanden 4 und 5 und ziehst sie in eine Klammer unter die Wurzel.

$\sqrt[\textcolor{blue}{3}]{\textcolor{red}{4}}\cdot\sqrt[\textcolor{blue}{3}]{\textcolor{red}{5}}= \sqrt[\textcolor{blue}{3}]{\textcolor{red}{4\cdot5}} = \sqrt[\textcolor{blue}{3}]{\textcolor{red}{20}}$

Wurzelgesetz dividieren

im Videozur Stelle im Video springen

Schauen wir uns auch zum Wurzel teilen die Wurzel Rechenregeln an. Genauso, wie bei der Multiplikation müssen die Wurzeln auch bei der Division den gleichen Wurzelexponenten n haben.

$\frac{\sqrt[\textcolor{blue}{n}]{\textcolor{red}{x}}}{\sqrt[\textcolor{blue}{n}]{\textcolor{red}{y}}} = \sqrt[\textcolor{blue}{n}]{\frac{\textcolor{red}{x}}{\textcolor{red}{y}}}$

Beispiel

Berechne die Division.

$\frac{\sqrt{\textcolor{red}{9}}}{\sqrt{\textcolor{red}{3}}}$

Beide Wurzeln haben den Exponenten 2 $(\sqrt[2]{x} = \sqrt{x})$ . Du kannst also die Radikanden 9 und 3 durcheinander teilen und unter eine Wurzel schreiben.

$\frac{\sqrt{\textcolor{red}{9}}}{\sqrt{\textcolor{red}{3}}} = \sqrt{\frac{\textcolor{red}{9}}{\textcolor{red}{3}}} = \sqrt{3}$

Mit Wurzeln rechnen: Wurzeln potenzieren

Auch zum Potenzieren gibt es Wurzelrechengesetze. Eine Wurzel als Potenz hat zusätzlich zum Wurzelexponenten n einen weiteren Exponenten m außerhalb der Klammer. Dann kannst du den Exponenten m unter die Wurzel ziehen.

$(\sqrt[n]{x})^{\textcolor{blue}{m}} = \sqrt[n]{x^\textcolor{blue}{m}}$

Beispiel

Potenziere die Wurzel $(\sqrt[3]{5})^{\textcolor{blue}{2}}$ .

Ziehe die 2 in die Wurzel und lass die Klammer weg.

$(\sqrt[3]{5})^{\textcolor{blue}{2}} = \sqrt[3]{5^\textcolor{blue}{2}} = \sqrt[3]{25}$

Wurzelgesetze: Wurzeln radizieren/auflösen

Die Wurzelregeln zum Radizieren verwendest du bei doppelten Wurzeln. Dazu multiplizierst du die Wurzelexponenten m und n miteinander und schreibst sie auf ein Wurzelzeichen. Die Zahl x unter der Wurzel übernimmst du.

$\sqrt[\textcolor{blue}{m}]{\sqrt[\textcolor{blue}{n}]{\textcolor{red}{x}}} = \sqrt[\textcolor{blue}{m} \cdot \textcolor{blue}{n}]{\textcolor{red}{x}}$

Beispiel

Radiziere folgende Wurzel.

$\sqrt{\sqrt[\textcolor{blue}{4}]{\textcolor{red}{28}}}$

Da auf der ersten Wurzel kein Exponent steht, ist es eine Quadratwurzel. Der Wurzelexponent ist also 2. Du multiplizierst daher die 2 mit der 4. Den Wert unter der Wurzel übernimmst du.

$\sqrt{\sqrt[\textcolor{blue}{4}]{\textcolor{red}{28}}} = \sqrt[\textcolor{blue}{2}]{\sqrt[\textcolor{blue}{4}]{\textcolor{red}{28}}} = \sqrt[\textcolor{blue}{2}\cdot \textcolor{blue}{4}]{\textcolor{red}{28}} = \sqrt[\textcolor{blue}{8}]{\textcolor{red}{28}}$

Wurzel als Potenz

im Videozur Stelle im Video springen

Manchmal ist es leichter, mit Potenzen zu rechnen, als mit Wurzeln. Wurzeln und Potenzen kannst du laut den Rechenregeln einfach umschreiben. Dabei wird der Exponent der Wurzel als Bruch dargestellt. Eine Wurzel mit einem Exponenten wandelst du als Potenz um, indem du den Wurzelexponenten n als Nenner in die Potenz schreibst. Als Zähler nimmst du den Exponenten m des Radikanden x. Falls der Radikand keinen Exponenten hat, ist m eine 1.

$\sqrt[\textcolor{blue}{n}]{\textcolor{red}{x}^\textcolor{teal}{m}} = \textcolor{red}{x}^{\frac{\textcolor{teal}{m}}{\textcolor{blue}{n}}}$

Beispiele

$\sqrt[\textcolor{blue}{5}]{\textcolor{red}{6}^\textcolor{teal}{2}} = \textcolor{red}{6}^{\frac{\textcolor{teal}{2}}{\textcolor{blue}{5}}}$

$\sqrt{\textcolor{red}{14}^{\textcolor{teal}{3}}} = \sqrt[\textcolor{blue}{2}]{\textcolor{red}{14}^\textcolor{teal}{3}} = \textcolor{red}{14}^{\frac{\textcolor{teal}{3}}{\textcolor{blue}{2}}}$

Quiz zum Thema Wurzelgesetze

Wurzeln und Potenzen

Du weißt nun, wie die Wurzelgesetze lauten und wie du mit Wurzeln rechnen kannst. Damit du verstehst, wie Potenzen und Wurzeln genau zusammenhängen, musst du unbedingt unser Video zu den Potenzgesetzen anschauen.

Potenzgesetze, Potenzregeln — Zum Video: Potenzgesetze

zur Videoseite: Wurzelgesetze

Beliebte Inhalte aus dem Bereich Mathematische Grundlagen

Kubikwurzel

Dauer: 02:31

Wurzeln addieren und subtrahieren

Wurzeln multiplizieren und dividieren

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .