Überschlagsrechnung
Du fragst dich, was ein Überschlag in der Mathematik ist und wofür er nützlich ist? Dann bist du hier genau richtig! Wir erklären dir alles, was du in der Mathematik zum Überschlag wissen musst. Sieh dir auch unser Video dazu an!
Inhaltsübersicht
Was ist eine Überschlagsrechnung?
Unter dem Überschlag in Mathe verstehst du das schnelle Abschätzen einer Aufgabe mit gerundeten Zahlen. Damit kannst du komplexe Rechnungen schnell überprüfen (z.B.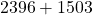 
).
Beim Überschlagen gehst du in zwei Schritten vor:
- Schritt: Du rundest
die Zahlen in der Aufgabe (z.B.
). - Schritt: Anschließend berechnest du die Aufgabe mit den gerundeten Zahlen (z.B.
).
Überschlag Addition
![\[\textcolor{red}{1296} + \textcolor{blue}{2343} =\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-4bfeb97e9769961e69c1f9a64080bf17_l3.png "Rendered by QuickLaTeX.com")
Die Aufgabe ist ganz schön kompliziert, um sie im Kopf zu berechnen, oder? Probiere es doch einmal mit der Überschlagsrechnung!
1. Schritt: Für das Rechnen mit Überschlag rundest zu zuerst beide Zahlen, die Summanden. Du entscheidest dich, auf Zehner zu runden.
![\[\textcolor{red}{1296} \approx \textcolor{red}{1300}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-c8012de870639f685163e29af638cafa_l3.png "Rendered by QuickLaTeX.com")
![\[\textcolor{blue}{2343} \approx \textcolor{blue}{2340}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-24b17c2cbf7b106dd5456967df6b09ad_l3.png "Rendered by QuickLaTeX.com")
Deine Aufgabe vom Anfang ist durch das Runden einfacher geworden:
![\[\textcolor{red}{1300} + \textcolor{blue}{2340} =\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-f6e50760ee7a35b3e8dd1474fb25e163_l3.png "Rendered by QuickLaTeX.com")
2. Schritt: Die gerundeten Zahlen kannst du jetzt einfach im Kopf addieren.
![\[\textcolor{red}{1300} + \textcolor{blue}{2340} = 3640\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-04c8476635cc1fa4a93dbae59f20d3b5_l3.png "Rendered by QuickLaTeX.com")
Überschlag Subtraktion
Überschlagen kannst du auch bei Minusaufgaben.
![\[\textcolor{red}{1441,1} - \textcolor{blue}{779,8} =\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-98b596659dcb24205a1c0983c16a3a9c_l3.png "Rendered by QuickLaTeX.com")
1. Schritt: Fürs Überschlagen in Mathe rundest du zuerst beide Zahlen. Dabei kommt es dir auf die Nachkommastellen und die Einerstelle nicht an.
![\[\textcolor{red}{1441,1} \approx 1440\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-9dccc0816ed123e2db88d3c4375da3ef_l3.png "Rendered by QuickLaTeX.com")
![\[\textcolor{blue}{779,8} \approx \textcolor{blue}{780} \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-3fe92241f4e49bae9271a88ae7c940d4_l3.png "Rendered by QuickLaTeX.com")
2. Schritt: Jetzt ist es viel einfacher, die Aufgabe zu lösen: Du ziehst von 1440 einfach 780 ab, das schaffst du im Kopf!
![\[\textcolor{red}{1440} - \textcolor{blue}{780} = 660\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-108772ed634d197957be8a6654f97229_l3.png "Rendered by QuickLaTeX.com")
Klasse, die komplizierte Minusaufgabe konntest du mit der Überschlagsrechnung schnell abschätzen!
Überschlag Multiplikation:
Der Überschlag in Mathe hilft dir auch bei der Multiplikation komplizierter Zahlen.
![\[\textcolor{red}{133.679} \cdot \textcolor{blue}{996}=\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-f6bf203a4e5b397c98a6dd7d375ab7c0_l3.png "Rendered by QuickLaTeX.com")
1. Schritt: Bei großen Zahlen kannst du auch auf die Hunderterstelle runden:
![\[\textcolor{red}{133.679} \approx \textcolor{red}{133.600} \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-45b75dcaacf8ebec1e571ae3263b3ba2_l3.png "Rendered by QuickLaTeX.com")
![\[\textcolor{blue}{996} \approx \textcolor{blue}{1000}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-3443edd3ef1db37e4a584a906ad8e9cd_l3.png "Rendered by QuickLaTeX.com")
2. Schritt: Und jetzt kannst du die Aufgabe berechnen, indem du im Kopf multiplizierst.
![\[\textcolor{red}{133.600} \cdot \textcolor{blue}{1000}= 133.600.000\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-04761b419a7c58c159139903de91a033_l3.png "Rendered by QuickLaTeX.com")
Du siehst, komplizierte Malaufgaben sind durch Überschlagen gut zu bewältigen!
Überschlagsrechnung Division:
Genau so gehst du bei Divisionsaufgaben vor.
![\[\textcolor{red}{754} : \textcolor{blue}{248}=\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-e8b104bfeb5f2b14072b77cfab296bd1_l3.png "Rendered by QuickLaTeX.com")
1. Schritt: Zuerst rundest du beide Zahlen auf Zehner.
![\[\textcolor{red}{754} \approx \textcolor{red}{750} \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-599e213cc488c5383a0c1aacf6d22ed3_l3.png "Rendered by QuickLaTeX.com")
![\[\textcolor{blue}{248} \approx \textcolor{blue}{250}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-7637a8fb56e00506db22b3130e26ffd4_l3.png "Rendered by QuickLaTeX.com")
2. Schritt: Nun kannst du ganz einfach dividieren:
![\[\textcolor{red}{750} : \textcolor{blue}{250}= 3\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-fb3181cef0cfc1cff7a7ea951c462a39_l3.png "Rendered by QuickLaTeX.com")
Spitze, die Überschlagsrechnung beherrscht du nun!
Überschlag zum Überprüfen von Rechnungen
Jetzt fragst du dich sicher: Wofür brauche ich den Überschlag in Mathe?
Es lohnt sich immer, komplizierte Rechnungen durch das Überschlag Rechnen zu überprüfen. Außerdem erlaubt die Überschlagsrechnung dir, schnell eine grobe Vorstellung vom Ergebnis zu bekommen. Sehen wir uns das an der Aufgabe von oben an:
Du kannst 754 : 248 mit dem Taschenrechner oder schriftliche Division rechnen und erhältst ein genaueres Ergebnis, nämlich 3,040322581. Aber das dauert viel länger! Und das Ergebnis der Überschlagsrechnung, 3, reicht häufig aus.
![\[\textcolor{red}{754} : \textcolor{blue}{248}= 3,0403...\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-2718d6398fa4ad3022b84dc709484149_l3.png "Rendered by QuickLaTeX.com")
![\[\textcolor{red}{750} : \textcolor{blue}{250}= 3 \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-2ae64e8e7bdeddeb5f81e87db4eb91a6_l3.png "Rendered by QuickLaTeX.com")
Du kannst dich im 1. Schritt entscheiden, auf welche Stelle du rundest. Rundest du auf die Einerstelle, wird dein Ergebnis ziemlich genau. Entscheidest du dich hingegen, auf die Hunderterstelle zu runden, ist dein Ergebnis weniger genau. Das siehst du gut an der folgenden Aufgabe:
![\[\textcolor{red}{3210,4} + \textcolor{blue}{1449}=4659,4\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-3a1e9f03727b91b53661e1449dd2e7b6_l3.png "Rendered by QuickLaTeX.com")
Auf die Einerstelle gerundet sieht die Aufgabe so aus:
![\[\textcolor{red}{3210} + \textcolor{blue}{144+}= 4659\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-a65b5dbf0417cb428ef81ddb83dbf7b6_l3.png "Rendered by QuickLaTeX.com")
Auf Hunderterstellen gerundet, hast du diese Zahlen:
![\[\textcolor{red}{3200} + \textcolor{blue}{1400} = 4600\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-e35c61d8a9333e70843cc69ca27b3d8d_l3.png "Rendered by QuickLaTeX.com")
Wenn du auf die Einerstelle rundest, ist dein Ergebnis genauer. Wenn du also möglichst genau sein willst, rundest du beim Überschlagen besser auf die Einerstelle. Soll es schneller gehen, rundest du auf größere Stellen.
An den Aufgaben hast du gesehen, dass das Überschlag rechnen in Mathe dir viel Zeit und Nerven spart!
Schriftliche Multiplikation
Manchmal reicht der Überschlag der Multiplikation aber nicht. Wenn du ein genaueres Ergebnis als beim Überschlagen haben willst, hilft dir nur die schriftliche Multiplikation . Schau gleich vorbei, um zu erfahren, wie du zwei Zahlen schriftlich multiplizierst.
