Du willst zum Thema Potenzgesetze Aufgaben mit Lösungen sehen? Dann bist du hier genau richtig! In unserem Video rechnen wir mit dir einige Aufgaben durch.
Potenzgesetze Aufgaben einfach erklärt
Um Potenzgesetze beim Lösen von Aufgaben anwenden zu können, solltest du die Regeln für das Rechnen mit Potenzen im Kopf haben.
Erinnerung:
xa · xb = x a + b an · bn = (a · b)n
xa : xb = xa – b an : bn = (a : b)n
(xa)b = xa · b ![x^{\frac{\textcolor{red}{m}}{\textcolor{blue}{n}}} = \sqrt[\textcolor{blue}{n}]{\textcolor{red}{m}}](https://blog.studyflix.de/wp-content/ql-cache/quicklatex.com-d4ecf85b4ad00e707007dc859a5ad645_l3.png "Rendered by QuickLaTeX.com")
Die Regeln erklären wir dir ausführlich in einem extra Video . Schau vorbei!
Potenzgesetze Aufgabe 1
Berechne mit Hilfe der Potenzgesetze:
a) 23 · 25
b) 32 · 32
c) 510 · 54
d) a3 · a5
Lösung Aufgabe 1
Bei diesen Aufgaben ist die Basis immer gleich. Weil die Potenzen multipliziert werden, kannst du die Exponenten einfach addieren.
a) 23 · 25 = 2(3 + 5) = 28 = 256
b) 32 · 32 = 3(2 + 2) = 34 = 81
c) 510 · 54 = 5(10 + 4) = 514 = 6 103 515 625
d) a3 · a5 = a(3 + 5) = a8
Potenzgesetze Aufgabe 2
Fasse zusammen.
a) 43 : 42
b) 
c) 
d) x7 : x2
Lösung Aufgabe 2
Wenn zwei Potenzen mit gleicher Basis dividiert werden, kannst du sie zusammenfassen und die Exponenten dabei voneinander abziehen.
a) 43 : 42 = 4(3-2) = 41 = 4
b) 
c) 
d) x7 : x2 = x(7 – 2) = x5
Potenzregeln Aufgabe 3
Fasse zusammen.
a) (23)4
b) (82)3
c) (45)2
d) (b2)7
Lösung Aufgabe 3
Die beiden Exponenten kannst du multiplizieren und so die Potenzen zusammenfassen.
a) (23)4 = 2(3 · 4) = 212 = 4 096
b) (82)3 = 8(2 · 3) = 86 = 262 144
c) (45)2 = 4(5 · 2) = 410 = 1 048 576
d) (b2)7 = b(2 · 7) = b14
Potenzgesetze Aufgabe 4
Fasse zusammen.
a) 23 · 53
b) 13 : 23
c) 72 · 102
d) 
e) a2 · b2
f) 
Lösung Aufgabe 4
In diesen Beispielen ist die Basis verschieden, aber die Exponenten sind jeweils gleich. Du kannst die entsprechenden Regeln anwenden und die Potenzen so zusammenfassen.
a) 23 · 53 = (2 · 5)3 = 103 = 1 000
b) 13 : 23 = (1 : 2)3 = 0,53 = 0,125
c) 72 · 102 = (7 · 10)2 = 702 = 4 900
d) 
e) a2 · b2 = (a · b)2
f) 
Potenzgesetze Aufgabe 5
Fasse zusammen, soweit möglich.
a) 
b) 
c) 
d) 
e) 
f) 
Lösung Aufgabe 5
In diesen Aufgaben brauchst du die Regeln für negative Exponenten und Brüche in Potenzen. So kommst du zu den folgenden Lösungen.
a) 
b) 
c) ![9^{\frac{1}{2}} = \sqrt[2]{9^1} = \sqrt{9} = 3](https://blog.studyflix.de/wp-content/ql-cache/quicklatex.com-263c5f198f0788f34e4bd25f9f262df3_l3.png "Rendered by QuickLaTeX.com")
d) ![4^{-\frac{2}{3}} = \frac{1}{\sqrt[3]{4^2}} = \frac{1}{\sqrt[3]{16}}](https://blog.studyflix.de/wp-content/ql-cache/quicklatex.com-cfa42da63e8ec5519fd91bf18182881c_l3.png "Rendered by QuickLaTeX.com")
e) 
f) ![y^{\frac{4}{5}} = \sqrt[5]{y^4}](https://blog.studyflix.de/wp-content/ql-cache/quicklatex.com-925b757813ce4a230702f2215364fb4b_l3.png "Rendered by QuickLaTeX.com")
Potenzregeln Aufgabe 6
Fasse zusammen soweit es geht.
a) 25 · 23 : 27
b)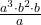 
c) 
d) 
Lösung Aufgabe 6
Bei diesen Aufgaben musst du verschiedene Regeln kombinieren.
a) 25 · 23 : 27 = 2(5 + 3 – 7) = 2(8 – 7) = 21 = 2
b) 
c) ![x^{-\frac{3}{2}} \cdot y^2:y = \frac{1}{\sqrt[2]{x^3}} \cdot y^{2 - 1} = \frac{1}{\sqrt{x^3}} \cdot y](https://blog.studyflix.de/wp-content/ql-cache/quicklatex.com-3f3c368b3275f46a1476627336e3d40f_l3.png "Rendered by QuickLaTeX.com")
d) 
Wurzelgesetze
Super! Du hast nun alle Aufgaben zu den Potenzgesetzen gelöst! Die Potenzgesetze hängen eng mit den Wurzelgesetzen zusammen. In unserem Video dazu erfährst du, welche Regeln es dazu gibt und wie du eine Wurzel in eine Potenz umrechnen kannst. Schau es dir gleich an!
