Brüche vergleichen und ordnen
Du willst Brüche vergleichen und ordnen? Hier findest du einfache Erklärungen, Beispiele und Übungsaufgaben. Schau dir auch unser Video dazu an!
Inhaltsübersicht
Gleichnamige Brüche vergleichen
Am einfachsten kannst du Brüche vergleichen, wenn sie den gleichen Nenner haben. Solche Brüche werden „gleichnamig“ genannt.
Um gleichnamige Brüche zu vergleichen, musst du nur auf den Zähler (die Zahl über dem Bruchstrich) schauen: Der Bruch mit dem größeren Zähler ist hier auch der größere Bruch.
![\[\frac{1}{4} < \frac{3}{4}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-35ec880b31dc9bd956f675dfdb4fe1b1_l3.png "Rendered by QuickLaTeX.com")
Beide Brüche haben den Nenner 4, daher musst du hier nur auf den Zähler achten: 3 ist größer als 1, also ist 
< 
.
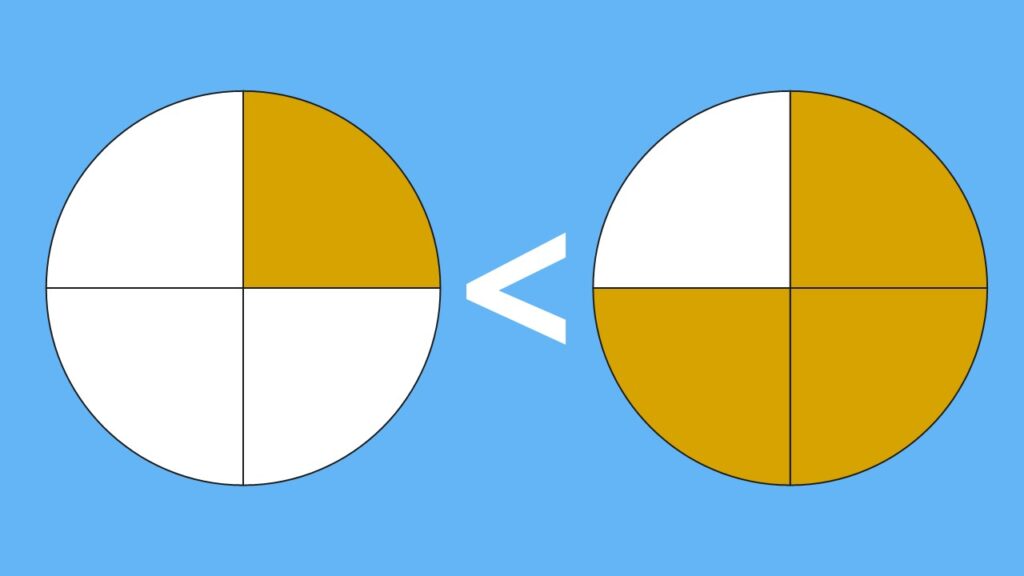
Das kannst du auch bei den Kreisdiagrammen sehen:
Bei sind mehr Felder ausgefüllt als bei .
Zählergleiche Brüche ordnen
Wenn Brüche den gleichen Zähler haben, bezeichnest du sie als zählergleich. Hier musst du zum Vergleichen auf den Nenner schauen: Der Bruch mit dem kleineren Nenner ist der größere Bruch.
![\[\frac{3}{8} < \frac{3}{6}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-38d54d49e429ba17fbb4c2c5baeeb8dc_l3.png "Rendered by QuickLaTeX.com")
Die beiden Brüche haben den gleichen Zähler, aber 8 ist größer als 6. Also ist 
< 
.
Das siehst du auch wieder in den Kreisdiagrammen:
Das erste Diagramm ist in acht Teile geteilt, das zweite in sechs. Bei dem ersten sind die Teile daher kleiner, als bei dem zweiten. Also ist dort weniger Fläche ausgefüllt.
Ungleichnamige Brüche vergleichen
Wenn Brüche nicht den gleichen Nenner haben, musst du sie zum Vergleichen auf den gleichen Nenner bringen. Dafür kannst du sie erweitern oder kürzen . Dann vergleichst du wieder die Zähler.
Vergleiche 
und 
.
- Zunächst musst du beide Brüche auf den gleichen Nenner bringen, in dem Fall 9. Das heißt, du erweiterst den ersten Bruch mit 3:
![\[\frac{2}{\textcolor{blue}{3}} \cdot \frac{\textcolor{teal}{3}}{\textcolor{teal}{3}} = \frac{2\cdot \textcolor{teal}{3}}{\textcolor{blue}{3} \cdot \textcolor{teal}{3}} = \frac{6}{\textcolor{red}{9}}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-d5d0c901dd1dfc0869c300f45196b488_l3.png "Rendered by QuickLaTeX.com")
- Jetzt haben beide Brüche den Nenner 9 und du kannst die Zähler vergleichen:
![\[\frac{6}{\textcolor{red}{9}} > \frac{4}{\textcolor{red}{9}} \quad\quad\rightarrow\quad\quad\frac{2}{3} > \frac{4}{9}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-434fe2bf81c2529648d3d3eb09f43d30_l3.png "Rendered by QuickLaTeX.com")
Sieh dir das wieder an den Kreisdiagrammen an:
Bei dem linken Kreis ist mehr Fläche ausgefüllt, als bei dem rechten.
Gemischte Brüche sortieren
Gemischte Brüche bestehen aus einer ganzen Zahl und einem echten Bruch. Bei so einem echten Bruch ist der Zähler kleiner als der Nenner.
Hier vergleichst du zunächst die ganzen Zahlen miteinander. Wenn eine von den ganzen Zahlen größer ist als die andere, kannst du sie sortieren. Auf den Bruch daneben musst du dabei nicht achten.
![\[2\frac{1}{4}< 4\frac{1}{10}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-a2dbd012b85b19b12830e35d8d60e439_l3.png "Rendered by QuickLaTeX.com")
Die beiden ganzen Zahlen vor den Brüchen sind unterschiedlich groß. Du schaust, welche davon größer ist und ordnest sie. 2 ist kleiner als 4. Deshalb ist 
.
Nur wenn die beiden ganzen Zahlen gleich groß sind, musst du die Brüche vergleichen.
![\[3\frac{1}{5} > 3\frac{1}{8}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-be83a14de0a2b8578a3a4cd118b7b059_l3.png "Rendered by QuickLaTeX.com")
Die beiden ganzen Zahlen vor den Brüchen sind gleich. Deshalb schaust du dir die Brüche an: 
und 
haben den gleichen Zähler, aber der Nenner von ist größer als der von . Deshalb ist 
und somit 3 
.
Brüche vergleichen — Übungen
- Vergleiche
und 
- Ordne
, 
und 
- Vergleiche und
- Sortiere 2 , 3 und 2
Lösungen:
-
< Beide Brüche haben den gleichen Nenner und 3 ist kleiner als 8.
-
< <Alle drei Brüche haben den gleichen Zähler und es gilt 6>5>3.
-
<Die Brüche musst du zunächst auf den gleichen Nenner bringen: 2/5 = 8/20 und 3/4=15/20. Es ist 8/20<15/20, also ist 2/5<3/4.
- 2 < 2 < 3 Du vergleichst die ganzen Zahlen: 3 ist größer als 2, deswegen ist 3 1/8 der größte von den drei gemischten Brüchen. Dann musst du 2 1/4 und 2 3/4 sortieren. Dazu vergleichst du die Brüche: 1/4 < 3/4 und damit 2 1/4 < 2 3/4.
Brüche vergleichen und ordnen — häufigste Fragen:
-
Wie vergleicht man Brüche?
Brüche mit demselben Nenner vergleicht man, indem man sich den Zähler anschaut: Der Bruch, mit dem größeren Zähler, ist hier auch der größere Bruch. Bei Brüchen mit demselben Zähler ist der Bruch mit dem kleineren Nenner der größere Bruch.
-
Wie findet man heraus, welcher Bruch größer und welcher kleiner ist?
Bei Brüchen mit dem gleichen Nenner ist der Bruch größer, der einen größeren Zähler hat. Bei Brüchen mit dem gleichen Zähler gilt: je kleiner der Nenner, desto größer der Bruch.
Bruch in Dezimalzahl
Jetzt weißt du, wie man Brüche miteinander vergleicht und ordnet. Du kannst Brüche auch vergleichen, in dem du sie in Dezimalzahlen umwandelst. Wie das geht, erfährst du hier.
