Video anzeigen

Hier geht's zum Video „Satz des Pythagoras“

Hier geht's zum Video „Satz des Pythagoras“

Satz des Pythagoras Aufgaben

Wichtige Inhalte in diesem Video

Hier haben wir zum Satz des Pythagoras Aufgaben mit Lösungen für dich zusammengetragen. Du möchtest Aufgaben Schritt für Schritt erklärt bekommen? Dann schau dir unser Video zum Satz des Pythagoras an!

Inhaltsübersicht

Aufgabe 1

im Videozur Stelle im Video springen

Formuliere den Satz des Pythagoras für die folgenden Dreiecke.

Satz des Pythagoras, Satz des Pythagoras Aufgabe, rechtwinkliges Dreieck, rechtwinklige Dreiecke — Aufgabe 1

Lösung Aufgabe 1

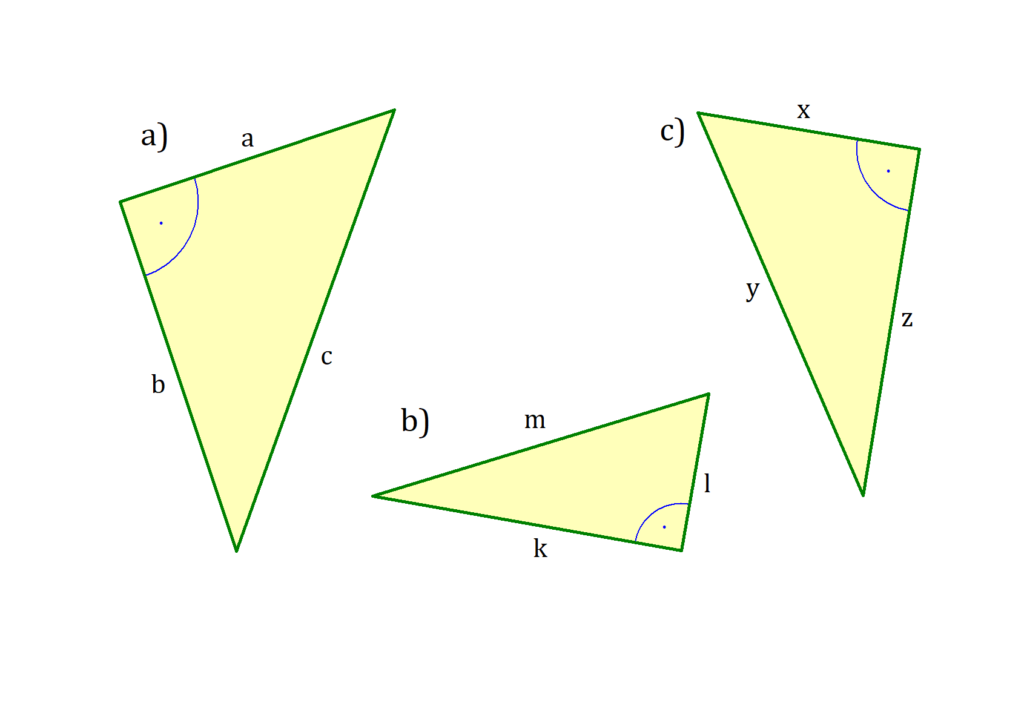
a) Der rechte Winkel liegt zwischen den Seiten a und b, deshalb sind diese die Katheten. Die Seite c liegt gegenüber vom rechten Winkel und ist deshalb die Hypotenuse des Dreiecks. Damit gilt a² + b² = c².

b) k²+ l² = m²

c) x²+ z² = y²

Aufgabe 2

im Videozur Stelle im Video springen

Berechne die fehlende Seitenlänge.

Satz des Pythagoras Aufgabe, Pythagoras Aufgabe, Aufgabe rechtwinkliges Dreieck — Aufgabe 2

Lösung Aufgabe 2

Mit der Formel von Pythagoras kannst du die gesuchten Seitenlängen berechnen, weil alle Dreiecke einen rechten Winkel haben.

Teilaufgabe a)

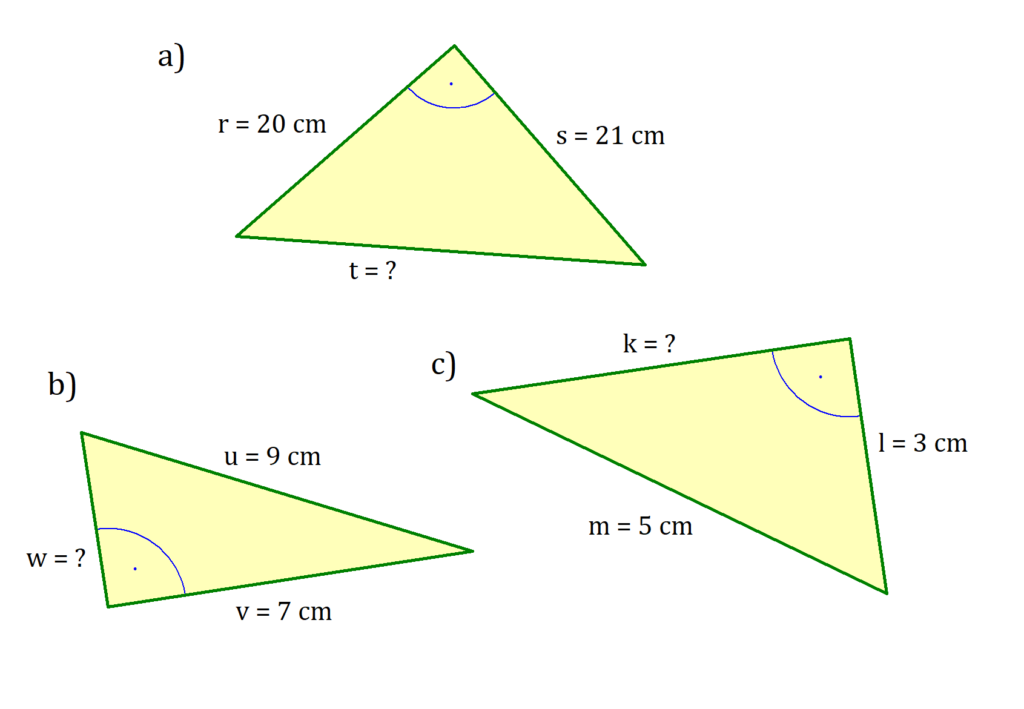
Die gesuchte Seite t ist die Hypotenuse des rechtwinkligen Dreiecks. Es gilt also

t² = r² + s²

Nun löst du die Formel nach t auf und setzt die Zahlen für r und s ein, um den gesuchten Wert für t zu berechnen.

$\begin{align*} t^2 &= r^2 + s^2 \\ t^2 &= (20\text{cm})^2 + (21\text{cm})^2 && | \sqrt{...} \\ t &= \sqrt{400\text{cm}^2 + 441 \text{cm}^2} \\ t &= \sqrt{841 \text{cm}^2} \\ t &= 29 \text{cm} \end{align*}$

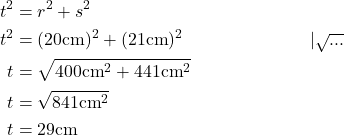
Teilaufgabe b)

Gesucht ist die Länge der Kathete w. Zuerst stellst du den Satz des Pythagoras auf und formst ihn um, sodass w auf einer Seite steht.

$\begin{align*} w^2+v^2 &= u^2 && | - v^2 \\ w^2 &= u^2 - v^2 && | \sqrt{...} \\ w &= \sqrt{u^2 - v^2} \end{align*}$

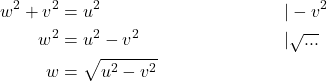
Jetzt setzt du nur noch die Werte ein und berechnest so die Länge von w.

$w = \sqrt{u^2-v^2} = \sqrt{(9\text{cm})^2 - (7\text{cm})^2} = \sqrt{81\text{cm}^2 - 49\text{cm}^2}$

$w = \sqrt{32 \text{cm}^2} = 4\sqrt{2} \text{cm} \approx 5,7 \text{cm}$

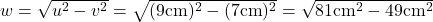
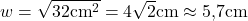
Teilaufgabe c)

Wieder wird nach einer Kathete gesucht. Durch Aufstellen und Umformen der Formel sowie das Einsetzen der Werte bekommst du die gesuchte Länge k.

$\begin{align*} k^2+l^2 &= m^2 && | - l^2 \\ k^2 &= m^2 - l^2 && | \sqrt{...} \\ k &= \sqrt{m^2 - l^2} \\ k&= \sqrt{(5\text{cm})^2 - (3\text{cm})^2} \\ k &= \sqrt{25\text{cm}^2-9\text{cm}^2} \\ k &= \sqrt{16\text{cm}^2} \\ k &= 4 \text{cm} \end{align*}$

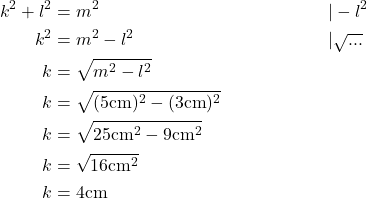
Aufgabe 3

im Videozur Stelle im Video springen

Häufig werden dir zum Satz des Pythagoras Textaufgaben gestellt. Schau dir mal eine dazu an:

In einem Flur mit einer Deckenhöhe von 2,40m sollen drei Meter lange Holzbalken möglichst senkrecht gelagert werden. Wie breit muss der Raum sein, damit die Holzbalken hinein passen?

Lösung Aufgabe 3

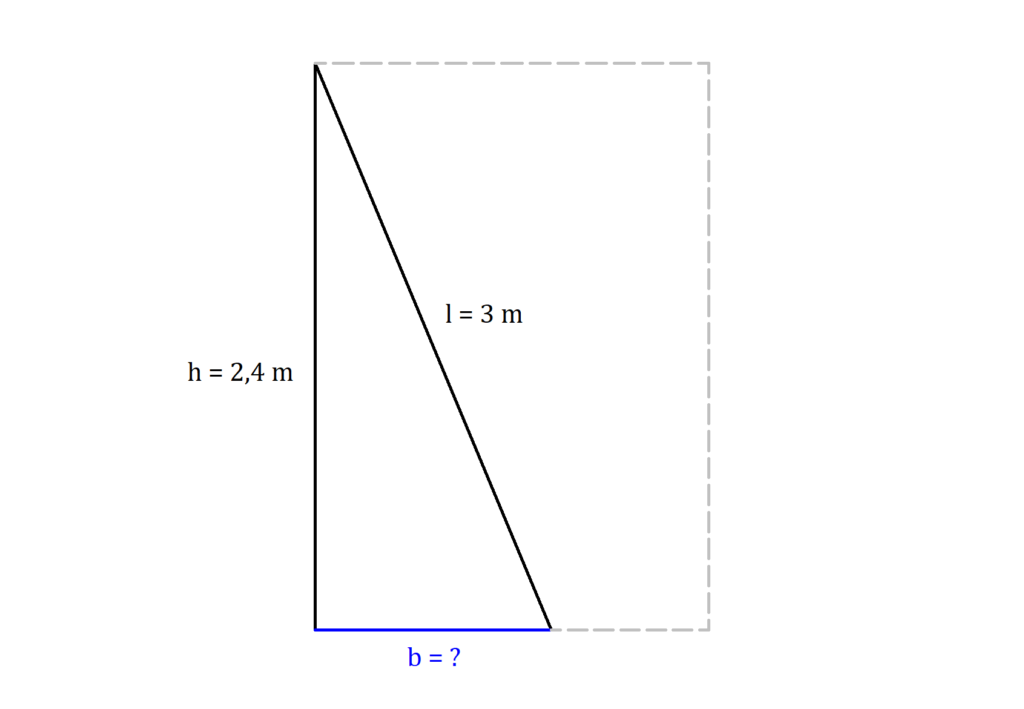
Am besten fertigst du dir bei Satz des Pythagoras Aufgaben zunächst einmal eine Skizze an und trägst gleich die Angaben ein, die du aus dem Text bekommen hast. Wichtig ist die Deckenhöhe von 2,40 m und die Länge der Holzbalken.

Satz des Pythagoras Aufgabe — Skizze Aufgabe 3

Gegeben: Deckenhöhe h = 2,4 m, Länge der Holzbalken l = 3 m, rechter Winkel zwischen h und b.

Gesucht: Mindestbreite b in Metern

Lösung:

Zunächst stellst du mit dem Pythagoras eine Formel auf.

h² + b² = l²

Diese löst du jetzt nach dem gesuchten b auf.

b^2 = l^2 - h^2

$b = \sqrt{l^2 - h^2}$

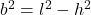
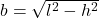
Nun musst du nur noch die Angaben einsetzen und kannst die gesuchte Breite so ausrechnen.

$b = \sqrt{ (3\text{m})^2 - (2,4\text{m})^2} = \sqrt{3,24} \text{m} = 1,8 \text{m}$

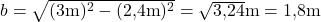
Antwort: Der Flur muss mindestens 1,8 m breit sein.

Aufgabe 4

Ganz oft gibt es zum Satz des Pythagoras Anwendungsaufgaben. Lass uns so eine Satz des Pythagoras Aufgabe gemeinsam durchgehen.

Ein Straßenschild zeigt an, dass auf den nächsten 800m eine Steigung von 10% herrscht. Wie groß ist der Höhenunterschied zwischen dem Beginn der Strecke und ihrem Endpunkt?

Lösung Aufgabe 4

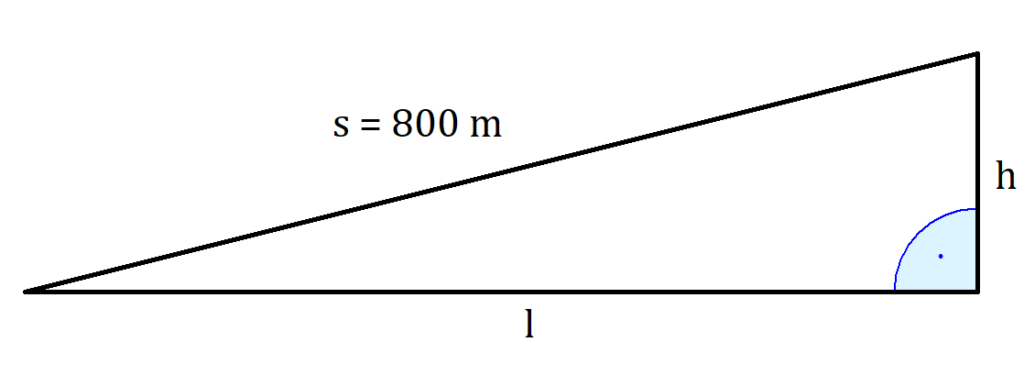
Auch hier hilft dir eine Skizze weiter, wie bei fast allen Satz des Pythagoras Aufgaben.

Satz des Pythagoras Aufgabe, Satz des Pythagoras Aufgaben, Aufgabe rechtwinkliges Dreieck — Skizze zu Aufgabe 4

Die Strecke s ist 800 m lang. Es herrscht eine Steigung von 10%. Das bedeutet

$\frac{h}{l} = \frac{10}{100}$ .

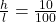Diese Gleichung kannst du nach dem gesuchten Höhenunterschied h auflösen.

$\begin{align*} \frac{h}{l} &= \frac{10}{100} && | \cdot l \\ h &= \frac{1}{10} \cdot l \end{align*}$

Außerdem gilt in diesem rechtwinkligen Dreieck

s^2 = h^2 + l^2 .

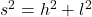Jetzt kannst du zunächst das h ersetzen und die Formel nach l auflösen.

$\begin{align*} s^2 &= h^2 + l^2 \\ s^2 &= \left({\frac{1}{10}}l\right)^2+l^2 \\ s^2 &= {\frac{1}{100}} l^2 + l^2 \\ s^2 &= 1,01 l^2 && | :1,01 \\ l^2 &= {\frac{s^2}{1,01}} && | \sqrt{...}\\ l &= \sqrt{\frac{s^2}{1,01}} \\ l &= \sqrt{\frac{(800\text{m})^2}{1,01}} \\ l &\approx 796 \text{m} \end{align*}$

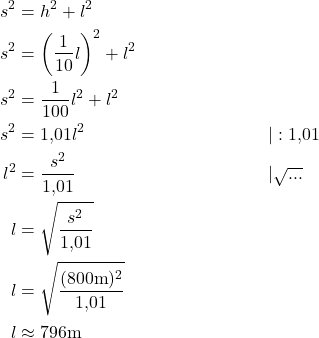
Diesen Wert für den horizontalen Weg l kannst du nun nutzen, um den Höhenunterschied h zu berechnen.

$h = \frac{1}{10} \cdot l = \frac{1}{10} \cdot 796 \text{m}$

$h \approx 79,6 \text{m}$

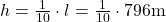
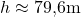
Antwort: Der Endpunkt der 800 Meter langen Strecke liegt also 79,6 m höher als der Startpunkt.

Aufgabe 5

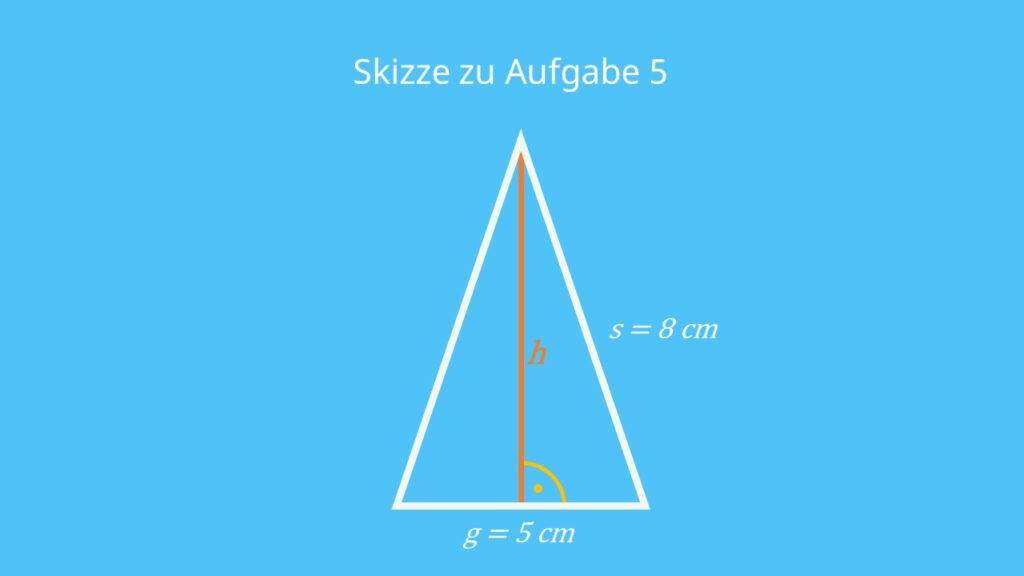
Ein gleichschenkliges Dreieck hat eine Grundseite g von 5 cm und Schenkel s von 8 cm. Berechne die Höhe des Dreiecks!

Lösung Aufgabe 5

Gegeben: Grundseite g = 5 cm, Schenkel s = 8 cm

Gesucht: Höhe h

In einem gleichschenkligen Dreieck steht die Höhe immer genau auf der Mitte der Grundseite. Die rechte Hälfte des gleichschenkligen Dreiecks ist also ein rechtwinkliges Dreieck mit

Hypotenuse s = 8 cm
Kathete h
Hälfte der Grundseite als andere Kathete, also (g : 2) = (5 cm : 2) = 2,5 cm

Satz des Pythagoras Aufgaben, pythagoras aufgaben, aufgaben satz des pythagoras, satz des pythagoras übungen, übungen satz des pythagoras, übungsaufgaben satz des pythagoras, satz des pythagoras textaufgaben, aufgaben pythagoras, satz des pythagoras aufgaben mit lösung, gleichschenkliges Dreieck, Höhe, Schenkel, rechtwinkliges Dreieck, rechter Winkel — Skizze zu Aufgabe 5

Der Satz des Pythagoras lautet also:

$\begin{align*} h^2 + (\frac{g}{2})^2&=s^2 \\ h^2 + (2,5\text{cm})^2&=(8\text{cm})^2 && | -(2,5\text{cm})^2 \\ h^2 &= (8\text{cm})^2 - (2,5\text{cm})^2&& | \sqrt{...} \\ h &= \sqrt{64\text{cm}^2 - 6,25\text{cm}^2} \\ h &= \sqrt{57,75\text{cm}^2} \approx 7,6\text{cm} \end{align*}$

Antwort: Die Höhe des Dreiecks beträgt ungefähr 7,6 cm.

Super! Schau dir jetzt noch drei weitere Übungen zum Satz des Pythagoras an!

Aufgabe 6

Überprüfe, ob folgende Dreiecke rechtwinklig sind:

a) a = 6 cm, b = 7 cm, c = 8,5 cm

b) u = 10 cm, v = 6 cm, w = 8 cm

Lösung Aufgabe 6

Teilaufgabe a)

Ein Dreieck ist dann rechtwinklig, wenn seine Seiten den Satz des Pythagoras erfüllen:

$\begin{align*} a^2 + b^2 &= c^2 \\ (6\text{cm})^2 + (7\text{cm})^2 &= (8,5\text{cm})^2 \\ 36\text{cm}^2 + 49\text{cm}^2 &= 72,25\text{cm}^2 \\ 85\text{cm}^2 &= 72,25\text{cm}^2 \implies FALSCH! \end{align*}$

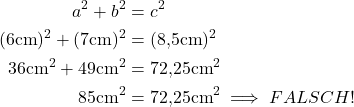
Antwort: Die letzte Gleichung stimmt nicht. Deshalb ist das Dreieck nicht rechtwinklig.

Teilaufgabe b)

Du setzt wieder in den Satz des Pythagoras ein. Die längste Seite, also hier u, ist dabei immer die Hypotenuse.

$\begin{align*} v^2 + w^2 &= u^2 \\ (6\text{cm})^2 + (8\text{cm})^2 &= (10\text{cm})^2 \\ 36\text{cm}^2 + 64\text{cm}^2 &= 100\text{cm}^2 \\ 100\text{cm}^2 &= 100\text{cm}^2 \implies RICHTIG! \end{align*}$

Antwort: Die letzte Gleichung stimmt. Deshalb ist das Dreieck rechtwinklig.

Prima! In Aufgabe 7 findest du nochmal zwei spannende Satz des Pythagoras Aufgaben mit Lösungen!

Aufgabe 7

Berechne die

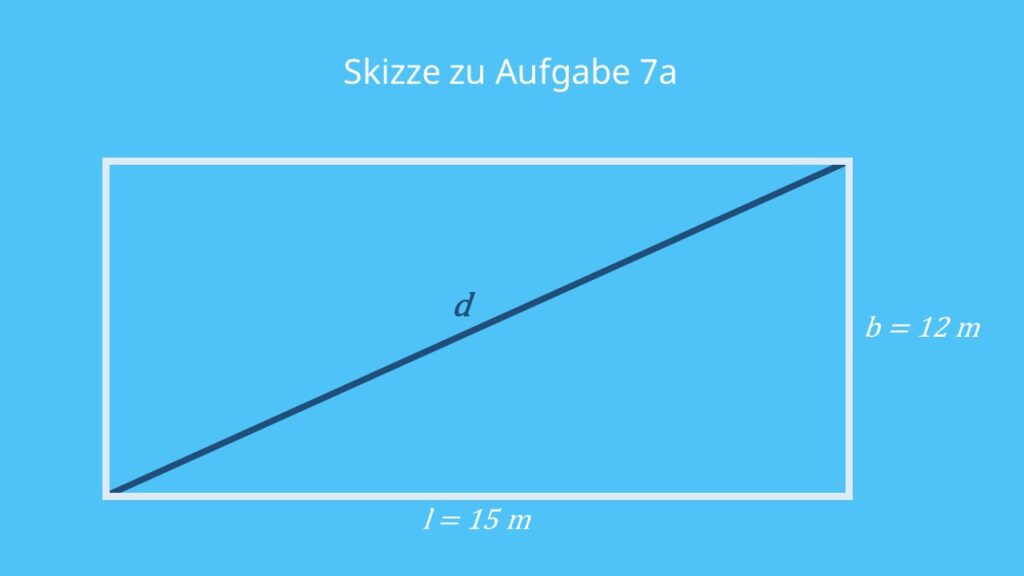
a) Diagonale eines Rechtecks mit den Seitenlängen l = 12 m und b = 15 m.

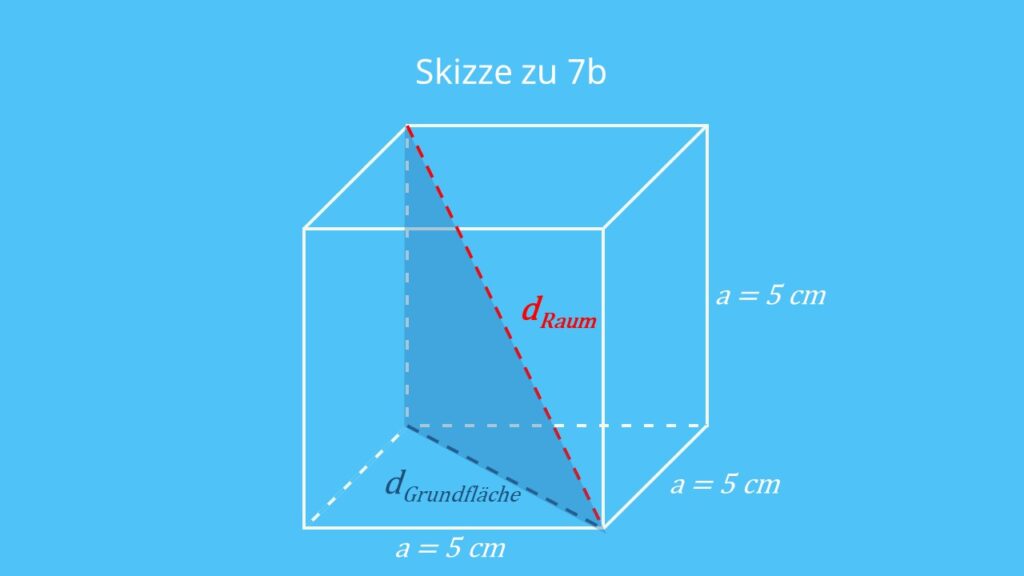
b) Raumdiagonale eines Würfels mit der Seitenlänge a = 5 cm.

Lösung Aufgabe 7

Teilaufgabe a)

Bei dieser Aufgabe hilft dir wieder eine Skizze.

Satz des Pythagoras Aufgaben, pythagoras aufgaben, aufgaben satz des pythagoras, satz des pythagoras übungen, übungen satz des pythagoras, übungsaufgaben satz des pythagoras, satz des pythagoras textaufgaben, aufgaben pythagoras, satz des pythagoras aufgaben mit lösung, Rechteck, Diagonale, Seiten, Länge, Breite — Skizze zu Aufgabe 7a

Du siehst ein rechtwinkliges Dreieck mit den Katheten l und b und der Hypotenuse d. Das setzt du in den Satz des Pythagoras ein:

$\begin{align*} l^2 + b^2 &= d^2 \\ (15\text{m})^2 + (12\text{m})^2 &= d^2 && |\sqrt{...} \\ \sqrt{(15\text{m})^2 + (12\text{m})^2} &= d \\ \sqrt{369\text{m}^2} &= d \\ d &\approx 19,2\text{m} \end{align*}$

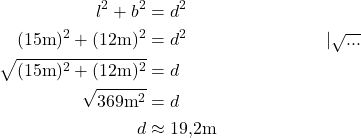
Antwort: Die Diagonale d ist ungefähr 19,2 m lang.

Teilaufgabe b)

Bei dieser Aufgabe gehst du am besten in zwei Schritten vor.

Schritt 1: Schau dir zunächst nur die Grundfläche des Würfels an. Die ist ein Quadrat mit 5 cm Seitenlänge. Du kannst also seine Diagonale berechnen wie in a):

$\begin{align*} a^2 + a^2 &= (d_{Grundfläche})^2 \\ (5\text{cm})^2 + (5\text{cm})^2 &= (d_{Grundfläche})^2 &&|\sqrt{...}\\ \sqrt{25\text{cm}^2 + 25\text{cm}^2} &= d_{Grundfläche} \\ \sqrt{50\text{cm}^2} &= d_{Grundfläche} \\ \end{align*}$

Satz des Pythagoras Aufgaben, pythagoras aufgaben, aufgaben satz des pythagoras, satz des pythagoras übungen, übungen satz des pythagoras, übungsaufgaben satz des pythagoras, satz des pythagoras textaufgaben, aufgaben pythagoras, satz des pythagoras aufgaben mit lösung, Würfel, Diagonale, Seite, Grundfläche, Raumdiagonale, Dreieck, rechtwinkliges Dreieck — Skizze zu Aufgabe 7b

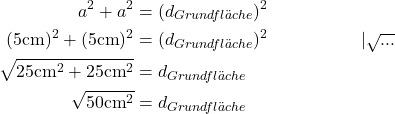
Schritt 2: Schau dir jetzt das markierte Dreieck im Raum an. Es ist rechtwinklig und eine Kathete ist die Diagonale der Grundfläche. Seine Hypotenuse ist die Raumdiagonale. Du kannst also den Satz des Pythagoras nochmal verwenden:

$\begin{align*} (d_{Grundfläche})^2 + a^2 &= (d_{Raum})^2 \\ (\sqrt{50\text{cm}^2})^2 + (5\text{cm})^2 &= (d_{Raum})^2 && |\sqrt{...} \\ \sqrt{50\text{cm}^2 + 25\text{cm}^2} &= d_{Raum} \\ \sqrt{75\text{cm}^2} &= d_{Raum} \\ 8,66\text{cm} &\approx d_{Raum} \end{align*}$

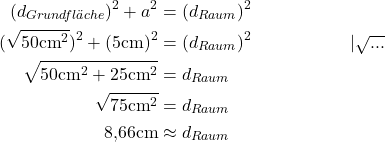
Antwort: Die Raumdiagonale des Würfels ist ungefähr 8,66 cm lang.

Kongruenzsätze

Super! Jetzt bist du fit in Übungsaufgaben und Textaufgaben zum Satz des Pythagoras! Mit dem Satz des Pythagoras kannst du nun ganz einfach fehlende Seitenlängen berechnen. Die brauchst du zum Beispiel, um herauszufinden, ob zwei Dreiecke genau aufeinander passen. Mithilfe der Kongruenzsätze kannst du überprüfen, ob zwei Dreiecke kongruent bzw. deckungsgleich sind. Wie das geht, zeigen wir dir im Video dazu. Schau es dir gleich an!

Kongruenzsätze, Kongruenz, kongruente Dreiecke, Kongruenzssatz SWS, SsW, SSWg, SSS, SSW, WSW, WWW, Kongruenzsatz SSW — Zum Video: Kongruenzsätze

Beliebte Inhalte aus dem Bereich Geometrie

Satz des Thales

Kongruenzsätze

Satz des Pythagoras

Satz des Pythagoras Aufgaben

Ankathete, Gegenkathete, Hypotenuse

Hypotenuse berechnen

Höhen- und Kathetensatz

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .