Video anzeigen

Hier geht's zum Video „Satz des Pythagoras“

Diagonale berechnen

Wichtige Inhalte in diesem Video

Was ist eine Diagonale?

Diagonale berechnen Rechteck

Diagonale Rechteck berechnen

Diagonale berechnen Quadrat

Du willst wissen, was eine Diagonale ist und wie du sie bei verschiedenen geometrischen Figuren berechnest? Hier und im Video erfährst du alles, was du wissen musst!

Inhaltsübersicht

Was ist eine Diagonale?

im Videozur Stelle im Video springen

Eine Diagonale verbindet zwei gegenüberliegende Ecken einer Figur. Dabei ist sie keine eigene Seite oder Kante, sondern führt durch die Form oder den Körper hindurch.

Diagonale, Flächendiagonale, Diagonale berechnen, Diagonale Rechteck, Diagonale Rechteck berechnen — Diagonale im Rechteck

In der Mathematik kürzt du die Diagonale mit einem d ab.

Diagonale berechnen Rechteck

im Videozur Stelle im Video springen

Ein Rechteck kannst du in zwei exakt gleich große, rechtwinklige Dreiecke teilen. Die längste Seite der Dreiecke nennst du auch Hypotenuse. Sie ist gleichzeitig die Diagonale d des Rechtecks.

Diagonale Rechteck Formel — Rechteck in zwei gleich große, rechtwinklige Dreiecke (weiß & türkis)

Um die Diagonale d zu berechnen, verwendest du den Satz des Pythagoras , denn er besagt:

(Länge a des Rechtecks)² + (Breite b des Rechtecks)² = (Diagonale)²
a² + b² = d²

Löst du die Gleichung nach der Diagonale d auf, indem du auf beiden Seiten die Wurzel ziehst, erhältst du die allgemeine Formel zum Diagonale berechnen:

a² + b² = d² | $\sqrt{\phantom{5}}$

→ $\textcolor{red}{d} = \sqrt{a^2 + b^2}$

Diagonale Rechteck berechnen

im Videozur Stelle im Video springen

Nun kennst du die Antwort auf die Frage: Was sind Diagonalen und wie berechne ich sie? Aber schauen wir uns zur Diagonale eines Rechtecks gleich mal ein Beispiel an. Denn mit der Formel ist die Berechnung der Diagonale wirklich einfach.

Beispielaufgabe

Gegeben ist ein Rechteck mit den Seitenlängen a = 4 cm und b = 3 cm. Nun sollst du die Diagonale des Rechtecks berechnen.

Diagonale Rechteck berechnen, Rechteck Diagonale berechnen, Diagonale berechnen Rechteck, Diagonale berechnen — Beispiel: Diagonale Rechteck berechnen

Gehe dabei wie folgt vor:

Formel aufstellen:

$\textcolor{red}{d} = \sqrt{a^2 + b^2}$

Angaben einsetzen:

$\textcolor{red}{d} = \sqrt{(4\text{cm})^2 + (3\text{cm})^2}$

Ergebnis berechnen:

$\textcolor{red}{d} = \sqrt{16\text{cm}^2 + 9\text{cm}^2} = \sqrt{25\text{cm}^2} = 5\text{cm}$

In diesem Rechteck ist die Diagonale insgesamt 5cm lang. Mit diesem Ablauf und der Formel kannst du in jedem beliebigen Rechteck die Diagonale berechnen.

Übrigens: In Rechtecken sind die Diagonalen immer gleich lang. Zudem halbieren sie sich gegenseitig.

Seitenlänge mit Diagonale berechnen

Du kannst aber auch aus einer gegebenen Diagonale eine fehlende Seitenlänge bestimmen. Dafür ist einerseits eine Seitenlänge a und andererseits die Länge der Diagonale d eines Rechtecks gegeben. Gesucht ist die Länge der Seite b.

Seitenlänge aus Diagonale berechnen, Rechteck Diagonale, Diagonale Rechteck — Seitenlänge aus Diagonale berechnen

Um diese Aufgabe zu lösen, stellst du die allgemeine Formel zum Diagonale berechnen nach der Seitenlänge b um:

$\textcolor{red}{d} = \sqrt{a^2+b^2}$

Formel umstellen:

$\begin{align*} \textcolor{red}{d} &= \sqrt{a^2 + b^2} && |...^2 \\ \textcolor{red}{d}^2 &= a^2 + b^2 && | - a^2 \\ \textcolor{red}{d}^2 - a^2 &= b^2 \\ b^2 &= \textcolor{red}{d}^2 - a^2 && |\sqrt{...} \\ b &= \sqrt{\textcolor{red}{d}^2 - a^2} \end{align*}$

Angaben einsetzen:

$b = \sqrt{(\textcolor{red}{9\text{cm}})^2 - (5\text{cm})^2}$

Ergebnis berechnen:

$b = \sqrt{81\text{cm}^2 - 25\text{cm}^2} = \sqrt{56\text{cm}^2} \approx 7,5\text{cm}$

Die Seitenlänge b ist circa 7,5 cm lang.

Diagonale berechnen Quadrat

im Videozur Stelle im Video springen

Ganz ähnlich funktioniert die Diagonale im Quadrat . Weil dort alle Seiten gleich lang sind (a=b), vereinfacht sich die Formel.

$\textcolor{red}{d} = \sqrt{a^2+a^2} = \sqrt{2 \cdot a^2} = \sqrt{2}\cdot a$

Diagonale Quadrat, Quadrat Diagonale, Diagonale eines Quadrats — Diagonale im Quadrat

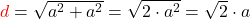
Damit kannst du nun ganz einfach die Diagonale im Quadrat berechnen.

Beispielaufgabe

Du sollst die Diagonale vom Quadrat mit der Seitenlänge a = 1 m berechnen.

Formel aufstellen:

$\textcolor{red}{d} = \sqrt{2} \cdot a$

Angabe einsetzen:

$\textcolor{red}{d} = \sqrt{2} \cdot 1\text{m}$

Ergebnis berechnen:

$\textcolor{red}{d}=\sqrt{2}\text{m}$

Diagonale berechnen – Raute

Eine Raute hat vier gleichlange Seiten a. Dabei sind jeweils die zwei gegenüberliegenden Seiten parallel und die jeweils gegenüberliegenden Winkel gleich groß.

Raute, Drachenviereck, Rhombus, Karo, Raute Diagonale berechnen — Raute

Achtung! Eine Raute kannst du zwar auch in zwei Dreiecke teilen, aber diese sind nicht rechtwinklig. Deshalb darfst du für die Berechnung der Diagonale auch nicht den Satz des Pythagoras verwenden!

Die Diagonalen einer Raute sind unterschiedlich lang und halbieren sich gegenseitig. Außerdem stehen sie rechtwinklig zueinander.

Teilst du die Raute aber in vier kleinere Dreiecke, wie die Diagonalen es dir vormachen, sind die Dreiecke rechtwinklig. Deshalb kannst du für die folgenden Rechnungen den Satz des Pythagoras verwenden.

Raute, Drachenviereck, Rhombus, Karo, Diagonalen Raute, Diagonale berechnen Raute, Diagonale e, Diagonale f — Raute mit Diagonalen

Da die zwei Diagonalen unterschiedlich lang sind, brauchst du zwei verschiedene Formeln. Die lange Diagonale nennst du e und die kürzere f.

Um die Länge der Diagonalen zu berechnen, wendest du den Satz des Pythagoras an einem der kleinen Dreiecke an. Die Hypotenuse des kleinen Dreiecks ist die Seite a. Die beiden anderen Seiten sind e/2 und f/2.

Setze deine Werte zuerst in die Formel für den Satz des Pythagoras ein:

$(\frac{e}{2})^{2}+(\frac{f}{2})^{2} = a^{2}$

Nun kannst die Formel nach den Diagonalen e und f umstellen. Wie das geht, zeigen wir dir in ausführlich in diesem Video .

$\textcolor{red}{\text{e}}=2\cdot \sqrt{a^{2}-(\frac{f}{2})^{2}}$

$\textcolor{blue}{\text{f}}=2\cdot \sqrt{a^{2}-(\frac{e}{2})^{2}}$

Um eine Diagonale auszurechnen, brauchst du immer die Länge einer Seite und der anderen Diagonale.

Beispielaufgabe

Eine Raute ist a = 9 cm und ihre Diagonale f ist 12 cm lang. Wie lang ist die Diagonale e?

Formel aufstellen:

$\textcolor{red}{\text{e}}=2\cdot \sqrt{a^{2}-(\frac{f}{2})^{2}}$

Angaben einsetzen:

$\textcolor{red}{\text{e}}=2\cdot \sqrt{9^{2}-(\frac{12}{2})^{2}}$

Ergebnis berechnen:

$\textcolor{red}{\text{e}}=2\cdot \sqrt{9^{2}-(\frac{12}{2})^{2}}$

$\textcolor{red}{\text{e}}=2\cdot \sqrt{81-6^{2}}$

$\textcolor{red}{\text{e}}=2\cdot \sqrt{81-36}$

$\textcolor{red}{\text{e}}=2\cdot \sqrt{45}$

$\textcolor{red}{\text{e}}=6 \sqrt{5}$

Die Diagonale e ist 6 $\sqrt{5}$ cm lang.

Diagonale berechnen – Parallelogramm

Ein Parallelogramm hat vier Seiten. Dabei sind nur die zwei gegenüberliegenden gleich lang und parallel. Auch hier gibt es eine lange Diagonale e und eine kurze f.

Parallelogramm, Parallelogramm Diagonalen berechnen, Diagonalen Parallelogramm berechnen — Parallelogramm mit Diagonalen

Schau dir als erstes die Berechnung der kurzen Diagonale f an:

Indem du im Parallelogramm links ein kleines Dreieck „abschneidest“, erhältst du ein rechtwinkliges Dreieck.

Parallelogramm, Parallelogramm Diagonalen berechnen, Diagonalen Parallelogramm berechnen — Parallelogramm Diagonale f berechnen

Jetzt brauchst du die Länge der Strecke m. Dazu wendest du bei deinem „abgeschnittenen“ Dreieck den Satz des Pythagoras an.

(Seite b)² = m² + (Höhe h)²

Wenn du nach m auflöst, erhältst du:

b² – h² = m²

→ m = $\sqrt{b^{2}-h^{2}}$

Mit diesem Wert kannst du nun das gelbe Dreieck betrachten und seine Hypotenuse berechnen, denn das ist gleichzeitig die Diagonale f, die du haben möchtest. Setze also a-m und h in den Satz des Pythagoras ein. Die Formel für die kurze Diagonale f in einem Parallelogramm ist somit:

f² = (a – m)² + h²

→ f = $\sqrt{(a - m)^{2}+h^{2}}$

Nun schauen wir uns an, wie du die lange Diagonale e berechnen kannst:

Für die Diagonale e schiebst du das kleine „abgeschnittene“ Dreieck von links auf die andere Seite und „klebst“ es an das Parallelogramm. Zusammengesetzt entsteht ein großes rechtwinkliges Dreieck. Seine längste Seite (Hypotenuse) ist gleichzeitig die Diagonale e.

Parallelogramm Diagonalen berechnen, Parallelogramm Diagonale e, Diagonale f, Parallelogramm Diagonalen berechnen — Parallelogramm Diagonale e berechnen

Rechne mit dem Satz des Pythagoras:

e² = (a + m)² + h²

→ e = $\sqrt{(a + m)^{2}+h^2}$

Beispielaufgabe

Ein Parallelogramm hat die Größen a = 10 cm, b = 7 cm und h = 5cm. Wie groß ist die kürzere Diagonale f?

Als erstes berechnest du m.

m = $\sqrt{b^{2}-h^{2}}$

m = $\sqrt{7^{2}-5^{2}}$

m = $\sqrt{49-25}$

m = $\sqrt{24}$

m ≈ 4,9

Jetzt verwendest du die Formel für die Diagonale f.

f = $\sqrt{(a-m)^{2}+h^{2}}$

f = $\sqrt{(10-4,9)^{2}+5^{2}}$

f = $\sqrt{26,01 + 25}$

f = $\sqrt{51,01}$

f ≈ 7,14

Die Diagonale f ist ungefähr 7,14 cm lang.

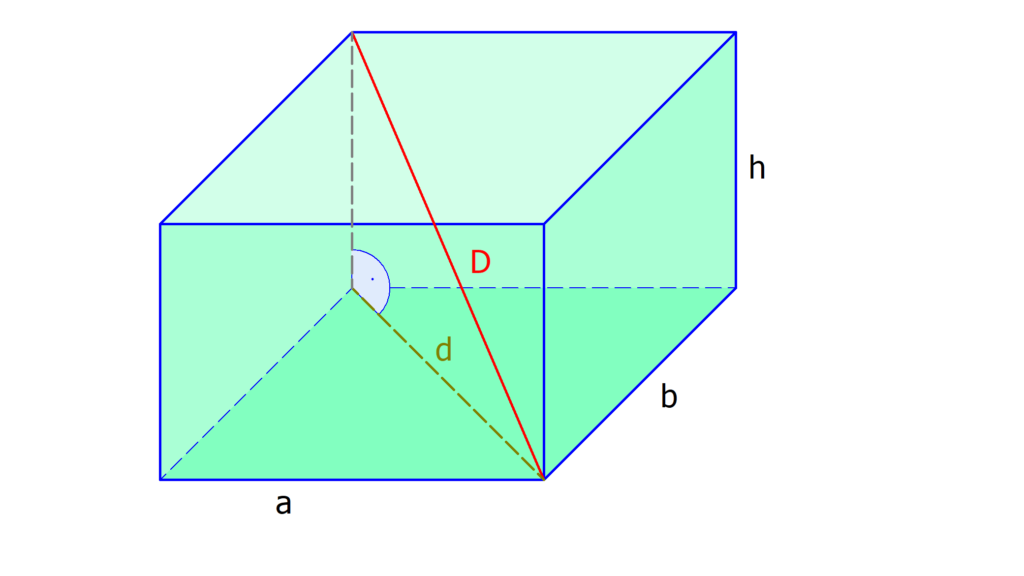
Diagonale berechnen – Quader

Ein Quader ist ein dreidimensionaler Körper . Er hat eine Länge a, eine Breite b und eine Höhe h und besteht aus sechs Seiten. Die gegenüberliegenden Seiten sind jeweils identisch.

Quader, Diagonalen Quader berechnen, Diagonale berechnen Quader — Quader mit Diagonale

Die vier Raumdiagonalen verbinden immer zwei Ecken miteinander und führen durch den Quader hindurch.

Um die Diagonale eines Quaders zu berechnen, verwendest du wieder den Satz des Pythagoras. Es reicht, wenn du eine Diagonale berechnest, denn im Quader sind sie alle gleich lang.

So gehst du dabei vor:

Stell dir vor, in deinem Quader steht aufrecht ein rechtwinkliges Dreieck. Du willst seine Hypotenuse berechnen, denn sie ist gleichzeitig die Raumdiagonale D des Quaders.

Quader, Diagonalen Quader berechnen, Diagonale berechnen Quader — Quader Diagonale berechnen

Für den Satz des Pythagoras brauchst du zum einen die Diagonale d der Grundfläche und zum anderen die Höhe des Quaders.

Da die Grundfläche ein Rechteck ist, berechnest du seine Diagonale d mit der Formel d = $\sqrt{a^{2}+b^{2}$

Nun kannst du ganz einfach die Diagonale D berechnen:

D² = d² + h²

D² = a² + b² + h²

D = $\sqrt{a^{2}+b^{2}+h^{2}$

Beispielaufgabe

Ein Quader hat die Größen a = 5 cm, b =4 cm und h = 3 cm. Wie groß ist seine Raumdiagonale D?

Formel aufstellen:

D = $\sqrt{a^{2}+b^{2}+h^{2}$

Eingaben einsetzen:

D = $\sqrt{5^{2}+4^{2}+3^{2}$

Ergebnis berechnen:

D = 5 $\sqrt{2}$

Die Raumdiagonale D ist 5 $\sqrt{2}$ cm lang.

Trapez – Flächeninhalt und Umfang

im Videozum Video springen

Jetzt kannst du die Diagonalen der verschiedensten geometrischen Figuren berechnen. Schau dir nun auch das Trapez an und wie du seinen Flächeninhalt und Umfang berechnest!

Zum Video: Trapez - Flächeninhalt und Umfang — Zum Video: Trapez – Flächeninhalt und Umfang

Beliebte Inhalte aus dem Bereich Geometrie

Diagonale berechnen

Parallelogramm - Flächeninhalt und Umfang

Haus der Vierecke

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .