Trapez – Flächeninhalt und Umfang

In diesem Beitrag erklären wir dir, was der Flächeninhalt beim Trapez ist und wie du die Trapez Fläche und den Umfang berechnen kannst. Du möchtest dir das lieber ansehen? In unserem Video erklären wir dir die Flächenberechnung im Trapez nochmal anschaulich und mit vielen Beispielen!

Inhaltsübersicht

Wie berechnet man den Flächeninhalt eines Trapez?
im Text
im Video
Trapez Flächeninhalt
im Text
im Video
Umfang Trapez
im Text
im Video
Flächeninhalt gleichschenkliges Trapez
im Text
Andere Formel Flächeninhalt Trapez berechnen
im Text
im Video
Andere Vierecke
im Text

Wie berechnet man den Flächeninhalt eines Trapez?

zur Stelle im Video springen

(00:12)

Bei einem Trapez können alle vier Seiten unterschiedlich lang sein. Allerdings gibt es immer zwei Seiten, die parallel zueinander sind.

Trapez, Flächeninhalt Trapez, Trapezfläche — Trapez

Hier sind die beiden Seiten a und c parallel zueinander. Außerdem brauchst du für die Flächenberechnung im Trapez die Höhe h. Du kannst dann den Flächeninhalt vom Trapez mit einer Formel berechnen.

$A = \frac{1}{2} \cdot (\textcolor{red}{a} + \textcolor{orange}{c}) \cdot \textcolor{blue}{h}$

Auch den Umfang vom Trapez kannst du mit einer Formel bestimmen.

$U=\textcolor{red}{a}+b+ \textcolor{orange}{c}+d$

Du musst also einfach alle Seiten zusammenzählen.

Trapez Flächeninhalt

zur Stelle im Video springen

(00:51)

Schauen wir uns am besten gleich mal ein paar Beispiele zum Trapez Flächeninhalt an.

Beispiel 1

Gegeben ist zur Berechnung vom Flächeninhalt ein Trapez mit den Seitenlängen $\textcolor{red}{a=10\text{cm}}$ und $\textcolor{orange}{c=4\text{cm}}$ sowie die Höhe $\textcolor{blue}{h=7\text{cm}}$ . Mit der Trapez Formel kannst du die Fläche von diesem Trapez schnell berechnen.

Flächeninhalt Trapez, Trapez Flächeninhalt, Trapezfläche Aufgabe — Trapez Beispiel 1

Formel aufstellen: Zuerst brauchst du die Formel für den Flächeninhalt vom Trapez.

$A = \frac{1}{2} \cdot (\textcolor{red}{a} + \textcolor{orange}{c}) \cdot \textcolor{blue}{h}$

Angaben einsetzen: Dann kannst du die gegebenen Werte für die Flächenberechnung im Trapez einfach einsetzen.

$A = \frac{1}{2} \cdot (\textcolor{red}{10\text{cm}} + \textcolor{orange}{4\text{cm}}) \cdot \textcolor{blue}{7\text{cm}}$

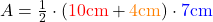
Ergebnis berechnen: Um abschließend die Trapezfläche zu bestimmen, musst du die Werte nur noch zusammenrechnen.

$A=\frac{1}{2} \cdot 14\text{cm} \cdot 7\text{cm} = 49\text{cm}^2$

Beispiel 2

Berechne den Flächeninhalt vom Trapez mit Seitenlänge $a=12\text{m}$ , $c=3\text{m}$ und Höhe $h=4\text{m}$ . Dafür nutzt du die Formel für die Trapezfläche.

Formel aufstellen:

$A=\frac{1}{2} \cdot (a+c) \cdot h$

Angaben einsetzen:

$A = \frac{1}{2} \cdot (12\text{m}+3\text{m}) \cdot 4\text{m}$

Ergebnis berechnen:

$A=\frac{1}{2} \cdot 15\text{m} \cdot 4\text{m} = 30\text{m}^2$

Die Grundfläche vom Trapez beträgt damit $30\text{m}^2$ .

Herleitung

Die Formel für die Fläche im Trapez kannst du dir auch selbst herleiten. Dazu startest du mit einem Trapez, das du gleich mal verdoppelst und umgedreht an das ursprüngliche Trapez anlegst.

So entsteht als Figur ein Parallelogramm . Die Grundseite dieser Figur ist $\textcolor{red}{a} + \textcolor{orange}{c}$ . Als nächstes zeichnest du die Höhe ein.

Flächeninhalt Trapez, Trapezfläche Herleitung, Flächeninhalt Trapez Herleitung — Herleitung Schritt 2

Auf diese Weise entsteht links das gelb eingefärbte Dreieck. Dieses kannst du nun gedanklich abschneiden und rechts an die Figur anlegen.

So bildest du ein Rechteck, das genauso groß ist wie zweimal das ursprüngliche Trapez. Diesen Flächeninhalt eines Rechtecks kannst du leicht berechnen.

$A_{Rechteck} = (\textcolor{red}{a} + \textcolor{orange}{c}) \cdot \textcolor{blue}{h}$

Um daraus die Formel für den Flächeninhalt vom Trapez zu gewinnen, musst du die Gleichung nur noch durch zwei teilen. So entsteht schlussendlich die Trapez Formel.

$A=\frac{1}{2} \cdot (\textcolor{red}{a} + \textcolor{orange}{c}) \cdot \textcolor{blue}{h}$

Mit dieser Formel kannst du ganz leicht jede Trapezfläche berechnen.

Umfang Trapez

zur Stelle im Video springen

(00:27)

Für den Umfang vom Trapez gibt es keine extra Formel, da alle vier Seiten unterschiedlich lang sein können. Um den Umfang in einem Trapez berechnen zu können, müssen also die Seitenlängen gegeben sein.

U = a + b + c + d

Umfang Trapez, Trapez Umfang — Umfang Trapez

Beispiel

zur Stelle im Video springen

(02:11)

In einem Trapez sind die Seitenlängen $a=10\text{cm}$ , $b=4\text{cm}$ , $c=3\text{cm}$ und $d=7\text{cm}$ gegeben. Du kannst den Umfang von diesem Trapez schnell berechnen.

Formel aufstellen:

U=a+b+c+d

Angaben einsetzen:

$U=10\text{cm}+4\text{cm}+3\text{cm}+7\text{cm}$

Ergebnis ausrechnen:

$U=24\text{cm}$

So kannst du den Umfang beim Trapez immer berechnen.

Flächeninhalt gleichschenkliges Trapez

Bei einem gleichschenkligen Trapez sind die zwei nicht parallelen Seiten gleich lang. Es gilt also b = d.

Eine extra Formel für den Flächeninhalt im gleichschenkligen Trapez gibt es aber nicht. Du verwendest für die Flächenberechnung im Trapez die schon bekannte Trapez Formel.

Beispiel

Gegeben ist für die Berechnung vom Flächeninhalt ein gleichschenkliges Trapez mit $a=11\text{cm}$ , $c=7\text{cm}$ und $h=6\text{cm}$ . Schritt für Schritt kannst du den Trapez Flächeninhalt berechnen.

Formel aufstellen:

$A=\frac{1}{2} \cdot (a+c) \cdot h$

Angaben einsetzen:

$A=\frac{1}{2} \cdot (11\text{cm} + 7\text{cm}) \cdot 6\text{cm}$

Ergebnis ausrechnen:

$A=\frac{1}{2} \cdot 18\text{cm} \cdot 6\text{cm} =54\text{cm}^2$

Die Fläche vom Trapez beträgt in diesem Beispiel also $54\text{cm}^2$ .

Andere Formel Flächeninhalt Trapez berechnen

zur Stelle im Video springen

(03:11)

Es gibt noch eine zweite Trapez Formel für den Flächeninhalt. Dabei nutzt du die Mittellinie $\textcolor{red}{m}$ zur Berechnung, die genau in der Mitte von a und c liegt.

Flächeninhalt Trapez, Trapez Flächeninhalt, Trapez Fläche — Trapez Fläche

Die Formel für den Flächeninhalt vom Trapez lautet dann

$A=\textcolor{red}{m} \cdot \textcolor{blue}{h}$ .

Lass uns auch zu dieser Formel im Trapez ein Beispiel machen.

Beispiel

Gegeben ist eine Mittellinie $\textcolor{red}{m=8\text{cm}}$ und eine Höhe $\textcolor{blue}{h=5\text{cm}}$ im Trapez.

Formel aufstellen:

$A=\textcolor{red}{m} \cdot \textcolor{blue}{h}$

Angaben einsetzen:

$A=\textcolor{red}{8\text{cm}} \cdot \textcolor{blue}{5\text{cm}}$

Ergebnis berechnen:

$A=40\text{cm}^2$

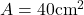
Mit beiden Trapez Formeln kannst du die Fläche vom Trapez schnell berechnen.

Andere Vierecke

Neben dem Trapez gibt es noch andere Vierecke, deren Flächeninhalt du berechnen kannst. Dazu gehört zum Beispiel das Rechteck oder das Parallelogramm .

Beim Trapez, Parallelogramm und Rechteck sind zwei Seiten parallel.
Beim Parallelogramm und Rechteck sind immer die zwei gegenüberliegenden Seiten parallel.
Bei einem Rechteck haben alle vier Winkel 90°.

Ein Parallelogramm ist also ein Spezialfall von einem Trapez. Schau dir gleich unser Video zum Flächeninhalt Parallelogramm an, um mehr über dieses besondere Viereck zu erfahren!

Geometrie

Dreiecke

Geometrie

Vierecke

Geometrie

Kreis

Geometrie

Geometrische Körper

Geometrie

Abstandsrechnung

Geometrie

Differentialgeometrie

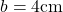Trapez – Flächeninhalt und Umfang

Wie berechnet man den Flächeninhalt eines Trapez?