Video anzeigen

Hier geht's zum Video „Oberfläche Kegel“

Volumen Kegel

Wichtige Inhalte in diesem Video

Volumen Kegel einfach erklärt

Hier erfährst du, was ein Kegel ist und wie du sein Volumen berechnest. In unserem Video rechnen wir dir alles Schritt für Schritt vor!

Inhaltsübersicht

Volumen Kegel einfach erklärt

im Videozur Stelle im Video springen

(00:13)

Ein Kegel ist ein geometrischer Körper . Im Alltag begegnen dir Kegel zum Beispiel in Form von Eiswaffeln oder Markierungshüten an Baustellen.

Ein Kegel hat immer eine Spitze und einen Kreis als Grundfläche. Die Kreislinie unten ist durch die Mantelfläche mit der Spitze verbunden.

Volumen Kegel, Kegel Volumen, Kegelvolumen — Volumen Kegel

Da der Kegel ein Körper ist, kannst du ihn zum Beispiel mit Wasser oder Luft befüllen. Wie viel davon in den Körper passt, sagt dir das Volumen.

Volumen Kegel berechnen

Das Kegel Volumen berechnest du mit der Formel

V = 1/3 · π · r² · h

Für das Volumen des Kegels rechnest du also 1/3 · Grundfläche · Höhe.

Volumen Kegel berechnen

Das Volumen eines Kegels kannst du in wenigen Schritten bestimmen. Für die Volumenformel vom Kegel brauchst du nur ein paar Angaben.

Beispiel

im Videozur Stelle im Video springen

(00:38)

Zuerst berechnen wir das Kegel Volumen von einem Kreiskegel mit Radius r = 5 cm und Höhe h = 10 cm.

Formel aufstellen: Zum Berechnen brauchst du die Formel für das Kegelvolumen.

V = 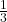$\frac{1}{3}$ · π · r² · h

Angaben einsetzen: Als nächstes verwendest du die Zahlenwerte aus der Angabe.

V = 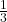$\frac{1}{3}$ · π · (5 cm)² · 10 cm

Ergebnis ausrechnen: Mit dem Taschenrechner kannst du dann das Kegel Volumen berechnen.

V = 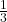$\frac{1}{3}$ · π ·25 cm² · 10 cm ≈ 261,8 cm³

Kegel Volumen Formel umstellen

Du kannst die Volumen Formel aber auch anders benutzen, um zum Beispiel aus dem Kegelvolumen den Radius vom Kegel zu berechnen. Dazu ist das Volumen eines Kegels V = 47,12 cm³ und die Höhe h = 5 cm gegeben.

Formel aufstellen: Zuerst schreibst du die Formel für das Volumen vom Kegel auf.

V = 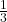$\frac{1}{3}$ · π · r² · h

Nach r auflösen: Nun formst du die Gleichung um, damit du den Radius berechnen kannst.

$\begin{align*} \frac{1}{3} \cdot \pi \cdot \textcolor{blue}{r}^2 \cdot \textcolor{red}{h} &= V && | \cdot 3 \\ \pi \cdot \textcolor{blue}{r}^2 \cdot \textcolor{red}{h} &= V \cdot 3 && | : \pi \\ \textcolor{blue}{r}^2 \cdot \textcolor{red}{h} &= \frac{3V}{\pi} && | : \textcolor{red}{h} \\ \textcolor{blue}{r}^2 &= \frac{3V}{\pi \cdot \textcolor{red}{h}} && | \sqrt{...} \\ \textcolor{blue}{r} &= \sqrt{ \frac{3V}{\pi \cdot \textcolor{red}{h}}} \end{align*}$

Angaben einsetzen: In diese Gleichung setzt du nun die Zahlenwerte ein.

$\textcolor{blue}{r} = \sqrt{\frac{3 \cdot 47,12\text{cm}^3}{\pi \cdot 5\text{cm}}}$

Radius berechnen: Zum Schluss tippst du alles in deinen Taschenrechner ein.

$\textcolor{blue}{r} = \sqrt{\frac{141,36\text{cm}^3}{15,71\text{cm}}} = \sqrt{9\text{cm}^2} = 3\text{cm}$

Anwendungsbeispiel

im Videozur Stelle im Video springen

(01:47)

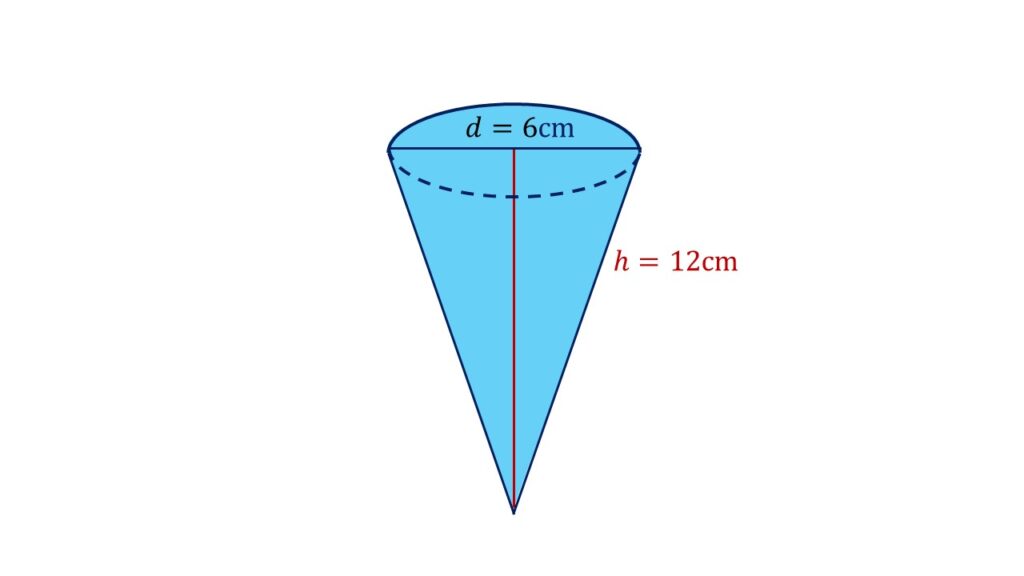
Für einen leckeren Nachtisch möchtest du eine Eiswaffel mit einer Vanillecreme füllen. Weil auch deine Freunde etwas abhaben wollen, machst du gleich 8 Stück davon. Jede Waffel hat einen Durchmesser von 6cm und ist 12cm hoch. Wie viel Eiscreme musst du machen, um alle 8 Eiswaffeln zu füllen?

Um die Antwort auf diese Frage zu finden, musst du das Volumen vom Kegel berechnen. Die Eiswaffel entspricht nämlich einem Kegel in der Geometrie. Für die Volumenberechnung vom Kegel bestimmst du aber erstmal den Radius aus dem Durchmesser.

$\textcolor{blue}{r} = \frac{d}{2} = \frac{6\text{cm}}{2} = 3\text{cm}$

Nun kannst du wie gewohnt das Kegel Volumen berechnen.

Formel aufstellen:

V = 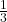$\frac{1}{3}$ · π · r² · h

Angaben einsetzen:

V = 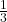$\frac{1}{3}$ · π · (3 cm)² · 12 cm

Ergebnis berechnen:

V = 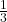$\frac{1}{3}$ · π · 9 cm² · 12 cm ≈ 113,1 cm³

Eine Eiswaffel hat also ein Kegelvolumen von V=113,1 cm³. Du machst allerdings insgesamt acht Waffeln. Deshalb musst du das Ergebnis noch mit 8 multiplizieren.

113,1 cm³ · 8 ≈ 905 cm³

Insgesamt musst du 905 cm³ Vanillecreme machen, um alle acht Waffeln damit zu füllen.

Oberfläche und Mantelfläche vom Kegel

Neben dem Kegelvolumen musst du auch häufig die Oberfläche von einem Kegel berechnen. Wie du die Formel für die Kegeloberfläche O = r² · π · + r · π · s anwendest, zeigen wir dir anhand von vielen Beispielen in unserem Video dazu.