Video

Quiz

Hier geht's zum Video „Flächeninhalt Kreis“

Hier geht's zum Video „Kreisberechnung“

Umfang Kreis

Wichtige Inhalte in diesem Video

Umfang Kreis berechnen einfach erklärt

Umfang Kreis berechnen mit Radius

Umfang mit Durchmesser berechnen

Umfang Kreis aus Flächeninhalt berechnen

Du willst wissen, wie du einen Kreis Umfang berechnen kannst? Hier und in unserem Video zeigen wir dir, wie’s geht!

Inhaltsübersicht

Umfang Kreis berechnen einfach erklärt

im Videozur Stelle im Video springen

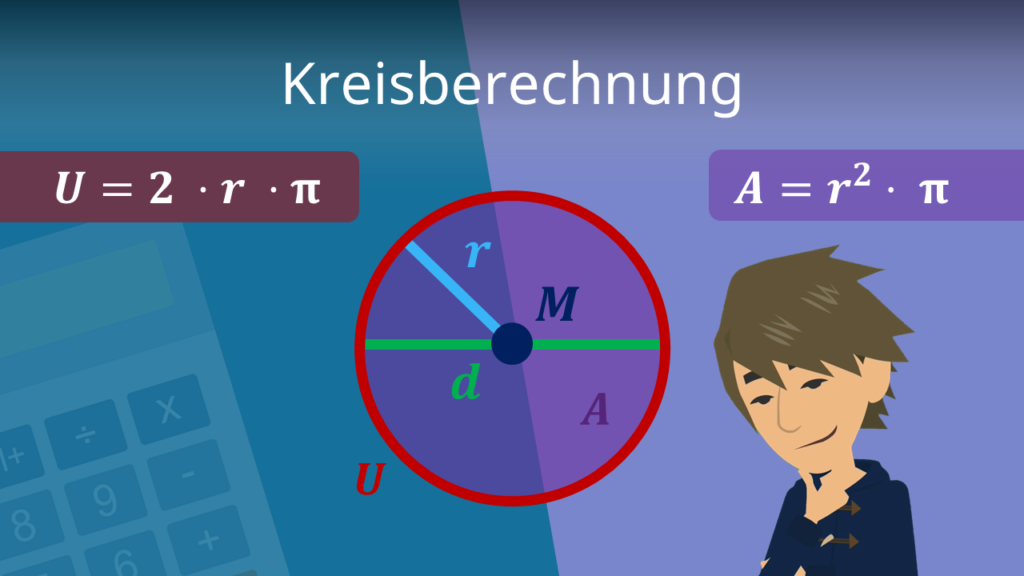
Ein Kreis ist eine runde geometrische Form. Du erkennst ihn daran, dass jeder Punkt auf der Kreislinie den gleichen Abstand zum Mittelpunkt M hat. Der Umfang U ist die Länge der Kreislinie.

Umfang Kreis, Kreis Umfang, Kreisumfang, Kreis — Umfang Kreis

Umfang Kreis Formel

Den Kreis Umfang berechnest du mit der Formel U = 2 · r · π oder U = d · π.

Um den Kreis Umfang zu berechnen, brauchst du den Radius r oder den Durchmesser d. Der Radius r ist der Abstand von einem Punkt auf der Kreislinie zum Mittelpunkt M.
Der Durchmesser d verbindet einen Punkt auf der Kreislinie mit dem direkt gegenüberliegenden. Er geht immer durch den Mittelpunkt M.

Wie du siehst, brauchst du außerdem für die Kreis Umfang Berechnung auch die Kreiszahl (Pi) π ≈ 3,1415. Sie ist in deinem Taschenrechner eingespeichert. Du kannst aber auch den gerundeten Wert verwenden.

Übrigens: Der Durchmesser d ist genau doppelt so lang, wie der Radius r (d = 2 · r).

Umfang Kreis berechnen mit Radius

im Videozur Stelle im Video springen

Dir werden immer wieder Aufgaben begegnen, bei denen du den Umfang des Kreises berechnen musst. Mit der Formel

$\textcolor{red}{U} = 2 \cdot \textcolor{blue}{r} \cdot \pi$

kannst du den Kreisumfang berechnen, wenn der Radius gegeben ist. Du musst den Wert dann nur in die Formel einsetzen und das Ergebnis bestimmen. Lass uns dazu gleich ein Beispiel machen.

Beispiel 1

Berechne den Umfang eines Kreises mit Radius $\textcolor{blue}{r= 4\text{cm}}$ .

Formel Umfang Kreis aufstellen: Zuerst schreibst du dir einmal die Formel auf.

$U = 2 \cdot \textcolor{blue}{r} \cdot \pi$

Angaben einsetzen: Jetzt setzt du den Wert für den Radius r ein.

$U = 2 \cdot \textcolor{blue}{4\text{cm}} \cdot \pi$

Ergebnis berechnen: Zum Schluss rechnest du die Werte nur noch zusammen und bekommst so den Kreis Umfang.

$U = 8\pi \text{cm} \approx 25,13\text{cm}$

Der Umfang vom Kreis beträgt also gerundet $U = 25,13\text{cm}$ .

Beispiel 2

Sehen wir uns gleich noch ein Beispiel an. Diesmal geht es um die Umfangsberechnung vom Kreis mit Radius $r = 2\text{m}$ .

Umfang Kreis Formel aufstellen: Auch hier schreibst du zuerst einmal die Formel auf.

$U = 2 \cdot r \cdot \pi$

Angaben einsetzen: Im nächsten Schritt ersetzt du das allgemeine r durch 2m.

$U = 2 \cdot 2\text{m} \cdot \pi$

Ergebnis berechnen: Abschließend musst du die Zahlen nur noch zusammenrechnen.

$U \approx 12,6 \text{m}$

Umfang mit Durchmesser berechnen

im Videozur Stelle im Video springen

Nicht immer hast du den Radius eines Kreises gegeben. Manchmal findest du stattdessen den Durchmesser d des Kreises.

Umfang Kreis, Kreis Umfang, Kreisumfang, Kreis Durchmesser — Kreis mit Durchmesser

Der Durchmesser d ist eine Strecke im Kreis, die genau doppelt so lang ist wie der Radius r

$\textcolor{orange}{d} = 2 \cdot \textcolor{blue}{r}$ .

Damit kannst du eine neue Formel für den Kreisumfang aufstellen.

$\textcolor{red}{U} = \underbrace{2 \cdot \textcolor{blue}{r}}_{=\textcolor{orange}{d}} \cdot \pi = \textcolor{orange}{d} \cdot \pi$

Lass uns auch dazu ein paar Beispiele machen.

Beispiel 1

Berechne den Umfang vom Kreis mit Durchmesser $\textcolor{orange}{d= 7\text{cm}}$ .

Kreisumfang Formel aufstellen: Weil du hier den Durchmesser gegeben hast, verwendest du die entsprechende Formel.

$U = \textcolor{orange}{d} \cdot \pi$

Angabe einsetzen: Den entsprechenden Wert setzt du nun ein.

$U = \textcolor{orange}{7\text{cm}} \cdot \pi$

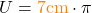
Ergebnis berechnen: Nun musst du nur noch die Zahlen zusammenrechnen, um den Umfang vom Kreis zu berechnen.

$U \approx 21,99\text{cm}$

Beispiel 2

Lass uns dazu gleich noch ein Beispiel machen. Du sollst den Umfang berechnen vom Kreis mit Durchmesser 10m.

Kreisumfang Formel aufstellen:

$U = d \cdot \pi$

Angaben einsetzen:

$U = 10\text{m} \cdot \pi$

Ergebnis berechnen:

$U \approx 31,42 \text{m}$

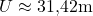
Mit diesen Schritten kannst du jeden Umfang mit dem Durchmesser berechnen.

Kreisumfang Halbkreis berechnen

Bisher hast du immer den Umfang vom gesamten Kreis bestimmt. Mit der Formel kannst du in wenigen Schritten aber auch den Umfang eines Halbkreises berechnen.

Umfang Halbkreis, Halbkreis, Halbkreis Umfang berechnen — Halbkreis

Zum Umfang des Halbkreises gehört die Linie des Kreisbogens und die gerade Linie unten, die gerade dem Durchmesser entspricht. Deshalb berechnest du diesen Umfang auch nicht nur mit einer Formel, sondern in mehreren Schritten.

Dafür sehen wir uns mal einen Halbkreis mit einem Durchmesser von 5 cm an.

Umfang Kreisbogen berechnen: Zuerst bestimmst du den gesamten Kreis Umfang mit der Formel und teilst diesen durch 2. So bekommst du die Länge des Kreisbogens.

$U_{\Kreisbogen} = \frac{1}{2} \cdot U_{\Kreis} = \frac{1}{2} \cdot d \cdot \pi$

$U_{\Kreisbogen} = \frac{1}{2} \cdot 5\text{cm} \cdot \pi \approx 7,85\text{cm}$

Umfang Halbkreis zusammensetzen: Jetzt kannst du den ganzen Umfang des Halbkreises berechnen, indem du den Umfang vom Kreisbogen mit dem Durchmesser zusammenrechnest.

$U_{\Halbkreis} = U_{\Kreisbogen} + d = 7,85\text{cm} + 5\text{cm} = 12,85\text{cm}$

Umfang Kreis aus Flächeninhalt berechnen

im Videozur Stelle im Video springen

Manchmal hast du in einer Aufgabe nicht direkt den Radius oder den Durchmesser eines Kreises gegeben. Du kannst aber auch aus dem Flächeninhalt den Umfang vom Kreis berechnen. Wie das genau funktioniert, wollen wir uns gleich mal an einem Beispiel ansehen.

Gegeben ist die Kreisfläche $A=314,16\text{cm}^2$ . Gesucht ist der Kreis Umfang.

Formel für den Flächeninhalt aufstellen: Zuerst schreibst du dir die Formel für den Flächeninhalt eines Kreises auf.

$A = r^2 \cdot \pi$

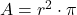
Formel nach r auflösen: Daraus möchtest du jetzt den Radius r berechnen. Dafür löst du die Formel einmal auf.

$\begin{align*} A &= r^2 \cdot \pi && | : \pi \\ \frac{A}{\pi} &= r^2 \\ r^2 &= \frac{A}{\pi} && | \sqrt{...} \\ r &= +\sqrt{ \frac{A}{\pi} } \end{align*}$

Beachte dabei, dass Längen immer als positive Zahl angegeben werden und du deshalb nur den positiven Wert aus der Wurzel verwendest.

Radius berechnen: Als Nächstes kannst du in die Formel die Angabe für den Flächeninhalt einsetzen und so den Radius des Kreises bestimmen.

$r=\sqrt{\frac{A}{\pi}} = \sqrt{\frac{314,16\text{cm}^2}{\pi}} = \sqrt{100\text{cm}^2} = 10\text{cm}$

Umfang Kreis Formel aufstellen: Ab hier kannst du wie gewohnt den Umfang vom Kreis berechnen.

$U = 2 \cdot r \cdot \pi$

Radius einsetzen:

$U = 2 \cdot 10\text{cm} \cdot \pi$

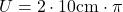
Kreisumfang berechnen:

$U \approx 62,83\text{cm}$

Hinweis: Zum Thema Flächeninhalt Kreis haben wir ein extra Video vorbereitet. Schau es dir gleich an!

Kreis, Flächeninhalt, Flächeninhalt Kreis, Flächeninhalt Kreis berechnen — Zum Video: Flächeninhalt Kreis

Expertenwissen: Geraden am Kreis

Jetzt weißt du, wie du den Kreisumfang berechnen kannst. Vielleicht kommen dir auch die Begriffe Passante, Sekante und Tangente bekannt vor. Hier siehst du, was es damit auf sich hat:

Geraden am Kreis, Passante, Tangente, Sekante — Geraden am Kreis

Einen Gerade,

nennst du Passante, wenn sie den Kreis an keinem Punkt schneidet.
nennst du Sekante, wenn sie den Kreis an genau zwei Punkten schneidet.
nennst du Tangente, wenn sie den Kreis an genau einem Punkt schneidet.

Umfang Kreis — häufigste Fragen

Was ist der Umfang eines Kreises?
Der Umfang eines Kreises ist die Länge der Kreislinie. Stell dir vor, du rollst einen Faden einmal um den Kreis herum. Die Länge des Fadens entspricht dann dem Umfang.
Wie berechnet man den Kreisumfang?
Den Kreisumfang kannst du auf zwei Weisen berechnen: Mit dem Radius U = 2 · r · π oder dem Durchmesser U = d · π.

Quiz zum Thema Umfang Kreis

Kreisberechnung

Super! Du kannst jetzt den Kreisumfang berechnen und kennst die Geraden am Kreis. Die anderen Kreisformeln sind übrigens noch:

Kreis Formel Durchmesser d = 2 · r
Kreis Formel Radius r = 1/2 · d
Kreis Formel Fläche A = π ·r² oder A = (π · d²) : 4 = π ·d² · 1/4

Wenn du sie dir genauer anschauen willst, haben wir ein extra Video für dich vorbereitet!

Kreisberechnung, Kreis, Berechnung Kreis, Formeln Kreis, Kreis Formel — Zum Video: Kreisberechnung

zur Videoseite: Umfang Kreis

Beliebte Inhalte aus dem Bereich Geometrie

Kreis berechnen

Kreisberechnung

Radius berechnen

Durchmesser berechnen

Flächeninhalt Kreis

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .