Video

Quiz

Hier geht's zum Video „Koordinatenform“

Hier geht's zum Video „Parameterform“

Hier geht's zum Video „Hessesche Normalform“

Schnittgerade zweier Ebenen

Wichtige Inhalte in diesem Video

Lagebeziehung Ebene-Ebene

Schnittgerade bestimmen

Zwei Ebenen können im Raum auf verschiedene Weise zueinander stehen. Mit folgenden Beispielen und unserem Videozeigen wir dir, wie du ihre Schnittgerade berechnest, falls sie sich schneiden.

Inhaltsübersicht

Lagebeziehung Ebene-Ebene

im Videozur Stelle im Video springen

Es gibt insgesamt drei Möglichkeiten, wie zwei Ebenen zueinander stehen können: Sie können identisch, parallel oder schneidend sein.

Sind zwei Ebenen identisch (a), liegen sie aufeinander und jeder Punkt, der in der ersten Ebene liegt, ist auch Teil der zweiten Ebene. Die Ebenen sind gleich.

Zwei Ebenen können auch parallel (b) sein. In diesem Fall haben die beiden Ebenen keine gemeinsamen Punkte. Jeder Punkt, der in der ersten Ebene liegt, kann kein Teil der zweiten Ebene sein.

Zuletzt können sich zwei Ebenen natürlich auch schneiden (c). Dabei liegen alle Punkte, die auf der Schnittgeraden zweier Ebenen liegen, sowohl in der ersten als auch der zweiten Ebene. Abgesehen davon besitzen die beiden Ebenen keine gemeinsamen Punkte.

Die folgenden Abschnitte zeigen dir, wie du herausfindest, ob die Schnittgerade zweier Ebenen existiert, und wie du sie findest.

Lagebeziehung Ebene Ebene, schnittgerade, schnittgerade ebene, parallele Ebenen, gleiche Ebenen — (a) zwei Ebenen sind identisch, (b) zwei Ebenen sind parallel, (c) zwei Ebenen schneiden sich in einer Schnittgeraden (grün)

Gegenseitige Lage von Ebenen

Das Ausrechnen der Schnittgerade zweier Ebenen kann dir viel über die Lage der Ebenen zueinander verraten. Deine Lösung der Geradengleichung kann einer von drei Fällen sein:

Erhältst du eine Geradengleichung als Lösung, weißt du, dass deine Ebenen sich schneiden und wo sie sich schneiden (Bild c).
Wenn du aber eine Lösung bekommst, die immer wahr ist – zum Beispiel — dann schneiden sie sich überall. Die Ebenen sind also identisch (Bild a).
Ist deine Lösung dagegen immer falsch – zum Beispiel 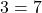— existiert keine Schnittgerade zweier Ebenen. Sie müssen also parallel sein (Bild b).

Es gibt viele mögliche Rechenwege, die Schnittgerade zweier Ebenen zu bestimmen. Abhängig von der Form, in der deine Ebenengleichungen geschrieben sind, ist mal die eine und mal die andere Variante schneller. Als nächstes zeigen wir dir, wie du die Schnittgerade zweier Ebenen berechnest, wenn beide Ebenen in Koordinatenform und wenn beide Ebenen in Parameterform vorliegen. Außerdem zeigen wir dir, wie du den Schnitt zweier Ebenen berechnest, wenn eine in Koordinaten- und die andere in Parameterform geschrieben ist.

Schnittgerade bestimmen

im Videozur Stelle im Video springen

Wie findest du die Schnittgerade zweier Ebenen, wenn beide in unterschiedlichen Formen geschrieben sind? ist in Koordinatenform und ist in Parameterform notiert. Der Trick, um dieses Problem zu lösen, ist das Einsetzen von in .

$\begin{align*} E&: 2 x_1 + 2 x_2 - 5 x_3 = -8 \\ F&: \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \\ 2 \end{pmatrix} + \lambda \begin{pmatrix} 3 \\ 0 \\ -1 \end{pmatrix} + \mu \begin{pmatrix} 2 \\ 1 \\ -1 \end{pmatrix} \end{align*}$

1.Schritt: Einsetzen der Parameterform in Koordinatenform

Wenn du die Parameter $\lambda$ und $\mu$ wieder in die Vektoren schreibst, erkennst du, dass die Parameterform aus drei Zeilen besteht. Jede Zeile ist eine Gleichung, mit der du einen Punkt auf der Ebene ausrechnen kannst. Diese drei Gleichungen – $\textcolor{violet}{x_1 = ...}$ , $\textcolor{teal}{x_2 = ...}$ und $\textcolor{brown}{x_3 = ...}$ – kannst du einfach in die Koordinatenform der Ebene einsetzen.

$\begin{array}{rl} E:& 2 \textcolor{violet}{x_1} + 2 \textcolor{teal}{x_2} - 5 \textcolor{brown}{x_3} = -8 \\ % F:& \begin{pmatrix} \textcolor{violet}{x_1} \\ \textcolor{teal}{x_2} \\ \textcolor{brown}{x_3} \end{pmatrix} = \begin{pmatrix} \textcolor{violet}{1} \\ \textcolor{teal}{0} \\ \textcolor{brown}{2} \end{pmatrix} + \begin{pmatrix} \textcolor{violet}{3\lambda} \\ \textcolor{teal}{0} \\ \textcolor{brown}{-\lambda} \end{pmatrix} + \begin{pmatrix} \textcolor{violet}{2\mu} \\ \textcolor{teal}{\mu} \\ \textcolor{brown}{-\mu} \end{pmatrix} \\ % \\[-2ex]\hline\\[-2ex] % F \,\text{in}\, E:& 2 \cdot \textcolor{violet}{(1 + 3\lambda + 2\mu)} + 2 \cdot \textcolor{teal}{(0 + 0 + \mu)} - 5\cdot \textcolor{brown}{(2 - \lambda - \mu)} = -8 \end{array}$

Vereinfache die Gleichung und du erhältst:

$\begin{array}{rcccl} F \,\text{in}\, E:& 2 \cdot \textcolor{violet}{(1 + 3\lambda + 2\mu)} &+\ 2 \cdot \textcolor{teal}{(0 + 0 + \mu)} &- \ 5\cdot \textcolor{brown}{(2 - \lambda - \mu)} &= -8 \\ & \textcolor{violet}{2 + 6\lambda + 4\mu} & \textcolor{teal}{+2 \mu} &\textcolor{brown}{-10 + 5 \lambda +5 \mu} &= -8 \\ & \multicolumn{3}{c}{-8 + 11\lambda + 11\mu} &=-8 \end{array}$

2.Schritt: Nach einem Parameter umstellen

Im ersten Schritt hast du eine Gleichung gefunden, die nur von $\lambda$ und $\mu$ abhängt. Als nächstes stellst du die Gleichung nach einem der beiden Parameter um. Wenn du die Gleichung nach $\mu$ umstellst, erhältst du dieses Ergebnis:

$\begin{alignat*}{3} -8 + 11\lambda +11\mu &= -8 &&\quad| +8 \\ 11\lambda + 11\mu &= 0 &&\quad| -11\lambda \\ 11\mu &= -11\lambda &&\quad| \cdot \nicefrac{1}{11} \\ \mu &= -\lambda \end{alignat*}\begin{align*}\end{align*}$

3.Schritt: Parameter in Parameterform einsetzen

Als nächstes setzt du deine Gleichung aus Schritt 2 in die Ebene ein, um die Gleichung der Schnittgeraden zu finden.

$\begin{alignat*}{3} F: \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} &= \begin{pmatrix} 1 \\ 0 \\ 2 \end{pmatrix} + \lambda \begin{pmatrix} 3 \\ 0 \\ -1 \end{pmatrix} \textcolor{blue}{+ \mu} \left \begin{pmatrix} 2 \\ 1 \\ -1 \end{pmatrix} \quad\right|&&\,\textcolor{blue}{\mu} = \textcolor{red}{-\lambda} \\ % \Rightarrow g: \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} &= \begin{pmatrix} 1 \\ 0 \\ 2 \end{pmatrix} + \lambda \begin{pmatrix} 3 \\ 0 \\ -1 \end{pmatrix} \textcolor{red}{-\lambda} \begin{pmatrix} 2 \\ 1 \\ -1 \end{pmatrix} \end{alignat*}\begin{align*}\end{align*}$

Vereinfache und du siehst, dass es sich tatsächlich um eine Geradengleichung in Parameterform handelt. Dafür klammerst du zuerst $\lambda$ aus den letzten beiden Termen aus und addierst die beiden Vektoren in der Klammer.

$\begin{align*} g: \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} &= \begin{pmatrix} 1 \\ 0 \\ 2 \end{pmatrix} + \lambda \left[ \begin{pmatrix} 3 \\ 0 \\ -1 \end{pmatrix} - \begin{pmatrix} 2 \\ 1 \\ -1 \end{pmatrix} \right] \\ % g: \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} &= \begin{pmatrix} 1 \\ 0 \\ 2 \end{pmatrix} + \lambda \left[ \begin{pmatrix} 3 - 2 \\ 0 -1 \\ -1 - (-1) \end{pmatrix} \right] \\[2ex] % g: \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} &= \begin{pmatrix} 1 \\ 0 \\ 2 \end{pmatrix} + \lambda \begin{pmatrix} 1 \\ -1 \\ 0 \end{pmatrix} \end{align*}$

Was hast du herausgefunden? Weil du den Schnitt zweier Ebenen und berechnen konntest, weißt du schon mal, dass sich die beiden Ebenen schneiden. Natürlich weißt du auch ganz genau, wo sie sich schneiden: Die beiden Ebenen und schneiden sich entlang ihrer Schnittgeraden .

Übung Schnittgeraden bestimmen

Gehe die Rechenschritte am besten noch mal selber durch. Hier sind noch mal zwei Ebenen E und F. Bestimme ihre Schnittgerade g!

$\begin{align*} E&: 5 x_1 - 3 x_2 + 2 x_3 = 20 \\ F&: \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} = \begin{pmatrix} 3 \\ 1 \\ 4 \end{pmatrix} + \lambda \begin{pmatrix} -2 \\ 5 \\ 2 \end{pmatrix} + \mu \begin{pmatrix} -1 \\ 2 \\ 2 \end{pmatrix} \end{align*}$

Setze als erstes die Ebene in ein und vereinfache die neue Gleichung. Dein Ergebnis sollte so aussehen:

$\text{F in E}:\, 20 - 21 \lambda - 7 \mu = 20$

Als nächstes stellst du diese Gleichung nach $\mu$ um. Ziehe dafür von beiden Seiten ab, addiere $7\mu$ und teile anschließend durch . Du erhältst dann:

$\mu = - 3 \lambda$

Zuletzt setzt du das in die Ebenengleichung von F ein. Danach kannst du noch $\lambda$ ausklammern und bekommst folgende Geradengleichung:

$g: \, \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} = \begin{pmatrix} 3 \\ 1 \\ 4 \end{pmatrix} + \lambda \begin{pmatrix} 1 \\ -1 \\ -4 \end{pmatrix}$

Schnittgerade zweier Ebenen Parameterform

Am einfachsten und schnellsten kannst du den Schnitt zweier Ebenen finden, wenn beide Ebenen in der Parameterform vorliegen. Du findest die Schnittgerade in nur drei Schritten. Der Trick ist, beide Ebenengleichungen gleich zu setzen. Folgendes Beispiel zeigt es dir mit den Ebenen und .

$\begin{align*} E&: \vec{x}(\lambda, \mu) = \begin{pmatrix} -1 \\ 2 \\ 0 \end{pmatrix} + \lambda \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} + \mu \begin{pmatrix} 2 \\ 0 \\ -1 \end{pmatrix} \\ F&: \vec{x}(s, t) = \begin{pmatrix} 2 \\ 1 \\ -2 \end{pmatrix} + s \begin{pmatrix} 0 \\ -1 \\ 3 \end{pmatrix} + t \begin{pmatrix} 2 \\ 2 \\ 0 \end{pmatrix} \end{align*}$

1.Schritt: Gleichsetzen der Ebenengleichungen

Weil beide Ebenengleichungen dieselbe Form haben, kannst du sie gleichsetzen. Dadurch findest du alle Punkte, die sowohl in $\textcolor{blue}{E}$ als auch in $\textcolor{red}{F}$ sind, das heißt, du findest die Schnittgerade zweier Ebenen.

$\begin{align*} \textcolor{blue}{E} = \textcolor{red}{F}&: \textcolor{blue}{ \begin{pmatrix} -1 \\ 2 \\ 0 \end{pmatrix} + \lambda \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} + \mu \begin{pmatrix} 2 \\ 0 \\ -1 \end{pmatrix} } = \textcolor{red}{ \begin{pmatrix} 2 \\ 1 \\ -2 \end{pmatrix} + s \begin{pmatrix} 0 \\ -1 \\ 3 \end{pmatrix} + t \begin{pmatrix} 2 \\ 2 \\ 0 \end{pmatrix} } \end{align*}$

Wenn du die Parameter $\lambda$ , $\mu$ , s und t in die Vektoren ziehst, siehst du, dass deine zwei Ebenengleichungen tatsächlich drei Gleichungen sind. Jede Zeile ist eine eigene Gleichung, die du im nächsten Schritt benutzen kannst, um die Schnittgerade zweier Ebenen zu finden.

$\begin{align*} E = F: \begin{pmatrix} \textcolor{violet}{-1} \\ \textcolor{teal}{2} \\ \textcolor{brown}{0} \end{pmatrix} + \begin{pmatrix} \textcolor{violet}{\lambda} \\ \textcolor{teal}{\lambda} \\ \textcolor{brown}{\lambda} \end{pmatrix} + \begin{pmatrix} \textcolor{violet}{2\mu} \\ \textcolor{teal}{0} \\ \textcolor{brown}{-\mu} \end{pmatrix} &= \begin{pmatrix} \textcolor{violet}{2} \\ \textcolor{teal}{1} \\ \textcolor{brown}{-2} \end{pmatrix} + \begin{pmatrix} \textcolor{violet}{0} \\ \textcolor{teal}{-s} \\ \textcolor{brown}{3s} \end{pmatrix} + \begin{pmatrix} \textcolor{violet}{2t} \\ \textcolor{teal}{2t} \\ \textcolor{brown}{0} \end{pmatrix} \\[1ex] \textcolor{violet}{-1 + \lambda + 2\mu} &= \textcolor{violet}{2 + 0 + 2t} \\ \textcolor{teal}{2 + \lambda + 0} &= \textcolor{teal}{1 - s + 2t} \\ \textcolor{brown}{0 + \lambda - \mu} &= \textcolor{brown}{-2 + 3s + 0} \end{align*}$

2.Schritt: Gleichungen nach einem Parameter auflösen

Als nächstes musst du deine Gleichungen aus Schritt 1 nach einem der vier Parameter $\lambda$ , $\mu$ , s oder t umstellen. Dazu suchst du dir zuerst eine Gleichung aus, die du gut nach einem Parameter auflösen kannst. In dieser Aufgabe kannst du zum Beispiel die dritte Gleichung nach $\mu$ auflösen, indem du zuerst beide Seiten mit $\lambda$ subtrahierst und danach ihr Vorzeichen umdrehst:

$\begin{array}{rcll} \textcolor{brown}{0 + \lambda - \mu} &=& \textcolor{brown}{-2 + 3s + 0} \\ \\[-2ex]\hline\\[-2ex] \textcolor{brown}{\lambda - \mu} &=& \textcolor{brown}{-2 + 3s } \quad& | -\lambda \\ \textcolor{brown}{- \mu} &=& \textcolor{brown}{-2 + 3s - \lambda} \quad& | \cdot (-1) \\ \textcolor{brown}{\mu} &=& \textcolor{brown}{+2 - 3s + \lambda} \end{array}$

Das Ergebnis kannst du danach für $\mu$ in der ersten Gleichung einsetzen. Die kannst du jetzt gut nach t auflösen.

$\begin{array}{rcll} \textcolor{violet}{-1 + \lambda + 2\mu} &=& \textcolor{violet}{2 + 0 + 2t} \\ \\[-2ex]\hline\\[-2ex] \textcolor{violet}{-1 + \lambda + 2 \cdot (2 - 3s + \lambda)} &=& \textcolor{violet}{2 + 2t } \quad& | -2 \\ \textcolor{violet}{-3 + \lambda + 2 \cdot (2 - 3s + \lambda)} &=& \textcolor{violet}{2t} \quad& | : 2 \\ \textcolor{violet}{-1.5 + 0.5\lambda + (2 - 3s + \lambda)} &=& \textcolor{violet}{t} \quad& | \text{ Klammer auflösen} \\ \textcolor{violet}{0.5 - 3s + 1.5\lambda} &=& \textcolor{violet}{t} \end{array}$

t setzte du jetzt in die zweite Gleichung ein. Jetzt kannst du die nach s auflösen.

$\begin{array}{rcll} \textcolor{teal}{2 + \lambda + 0} &=& \textcolor{teal}{1 - s + 2t} \\ \\[-2ex]\hline\\[-2ex] \textcolor{teal}{2 + \lambda} &=& \textcolor{teal}{1 - s + 2 \cdot (0.5 - 3s + 1.5 \lambda)} \quad& | \text{ Klammer auflösen} \\ \textcolor{teal}{2 + \lambda} &=& \textcolor{teal}{1 - s + 1 - 6s + 3 \lambda} \quad& | - 3 \lambda \\ \textcolor{teal}{2 - 2 \lambda} &=& \textcolor{teal}{2 - 7s} \quad& | - 2 \\ \textcolor{teal}{-2 \lambda} &=& \textcolor{teal}{- 7s} \quad& | : (-7) \\ \textcolor{teal}{\frac{2}{7}\lambda} &=& \textcolor{teal}{s} \end{array}$

Jetzt hast du die drei Gleichungen nach den drei Parametern $\mu$ , s und t aufgelöst. Jetzt kannst Du alle Gleichungen durch den vierten Parameter $\lambda$ darstellen.

3.Schritt: Parameter in Ebenengleichung einsetzen

Zuletzt muss du nur noch dein Ergebnis aus Schritt 2 in einer der Ebenengleichungen, zum Beispiel , einsetzen. Dadurch erhältst du eine Geradengleichung . Die Gerade ist die Schnittgerade zweier Ebenen, die du suchst.

$\begin{alignat*}{3} E: \vec{x} &= \begin{pmatrix} -1 \\ 2 \\ 0 \end{pmatrix} + \lambda \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} + \textcolor{red}{\mu} \left \begin{pmatrix} 2 \\ 0 \\ -1 \end{pmatrix} \; \; \qquad\qquad\qquad\right|&&\,\textcolor{red}{\mu} =\textcolor{blue}{2 - 3s + \lambda} \\ E: \vec{x} &= \begin{pmatrix} -1 \\ 2 \\ 0 \end{pmatrix} + \lambda \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} + \textcolor{blue}{(2 - 3s + \lambda)} \left \begin{pmatrix} 2 \\ 0 \\ -1 \end{pmatrix} \qquad\right|&&\,\textcolor{blue}{s} =\textcolor{blue}{\frac{2}{7} \lambda} \\ \Rightarrow g: \vec{x} &= \begin{pmatrix} -1 \\ 2 \\ 0 \end{pmatrix} + \lambda \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} + \textcolor{blue}{\left(2 + \frac{1}{7} \lambda\right)} \cdot \begin{pmatrix} 2 \\ 0 \\ -1 \end{pmatrix} \end{alignat*}\begin{align*}\end{align*}$

Wenn du die Gleichung vereinfachst, erkennst du, dass es sich bei tatsächlich um eine Geradengleichung handelt. Vereinfache, indem du die Klammer ausmultiplizierst.

$\begin{align*} g: \vec{x} &= \begin{pmatrix} -1 \\ 2 \\ 0 \end{pmatrix} + \lambda \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} + \textcolor{blue}{2 \cdot \begin{pmatrix} 2 \\ 0 \\ -1 \end{pmatrix}} \textcolor{blue}{+ \frac{1}{7}\lambda \cdot \begin{pmatrix} 2 \\ 0 \\ -1 \end{pmatrix} } \\ g: \vec{x} &= \begin{pmatrix} -1 \\ 2 \\ 0 \end{pmatrix} + \lambda \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} + \textcolor{blue}{ \begin{pmatrix} 4 \\ 0 \\ -2 \end{pmatrix} } \textcolor{blue}{+ \lambda \begin{pmatrix} \frac{2}{7} \\ 0 \\ -\frac{1}{7} \end{pmatrix} } \end{align*}$

Danach kannst du $\lambda$ wiederum ausklammern und die Vektoren addieren .

$\begin{align*} g: \vec{x} &= \begin{pmatrix} -1 \\ 2 \\ 0 \end{pmatrix} + \textcolor{blue}{ \begin{pmatrix} 4 \\ 0 \\ -2 \end{pmatrix} }+ \lambda \cdot \left[ \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} \textcolor{blue}{ + \begin{pmatrix} \frac{2}{7} \\ 0 \\ -\frac{1}{7} \end{pmatrix} }\right] \\[2ex] g: \vec{x} &= \begin{pmatrix} 3 \\ 2 \\ -2 \end{pmatrix} + \lambda \begin{pmatrix} \frac{9}{7} \\ 1 \\ \frac{6}{7} \end{pmatrix} \end{align*}$

Und Voilà, du hast die Schnittgerade zweier Ebenen gefunden! Weil du den Schnitt zweier Ebenen und berechnen konntest, weißt du jetzt, dass sich die beiden Ebenen schneiden. Außerdem kannst du auch sagen, wo sie sich schneiden: Die beiden Ebenen und schneiden sich entlang ihrer Schnittgeraden .

Schnittgerade zweier Ebenen Koordinatenform

Falls beide Ebenen in Koordinatenform vorliegen, brauchst du nicht erst eine Ebene von der Koordinatenform in Parameterform umrechnen. Du kannst dir direkt ein Gleichungssystem bauen. Die Lösung des Gleichungssystems ist dann die Schnittgerade zweier Ebenen. Schau dir das am besten an einem Beispiel an: Gegeben sind die Ebenen und in Koordinatenform. Zusammen kannst du beide Ebenen als Gleichungssystem sehen.

$\begin{align*} E: 2 x_1 - 3 x_2 - x_3 &= 8 \\ F: 6 x_1 + 3 x_2 + x_3 &= 0 \end{align*}$

1.Schritt: Lineares Gleichungssystem vereinfachen

Bisher ist das Gleichungssystem zu kompliziert. Mit dem Additionsverfahren kannst du es vereinfachen. Addiere dafür jeweils die rechten und linken Seiten der Gleichungen. Wenn du eine Erinnerungsstütze brauchst, schau dir unser Video zum Additionsverfahren an! Du bekommst dann Folgendes heraus:

$\textcolor{blue}{E}+\textcolor{red}{F}: \textcolor{blue}{2 x_1 - 3 x_2 - x_3} + \textcolor{red}{6 x_1 + 3 x_2 + x_3} = \textcolor{blue}{8} + \textcolor{red}{0}$

Sortiere die Terme um und du siehst, dass sich viel vereinfachen lässt.

$\begin{array}{ccccc l} (\textcolor{blue}{2x_1} \ \textcolor{red}{ + \ 6 x_1} ) &+& ( \textcolor{blue}{ - \ 3 x_2} \ \textcolor{red}{ + \ 3 x_2} ) &+& ( \textcolor{blue}{ - \ x_3} \ \textcolor{red}{ + \ x_3} ) &= \textcolor{blue}{8} + \textcolor{red}{0} \\ 8 x_1 &+& 0 x_2 &+& 0 x_3 &= 8 \end{array}$

Falls du es mal mit schwierigeren Ebenen zu tun haben solltest, kannst du dein Wissen über lineare Gleichungssysteme mit unserem Video auffrischen. In diesem Beispiel bleibt jedoch nur x_1 am Ende stehen und du hast die erste Lösung deines Gleichungssystems gefunden:

$\begin{align*} 8x_1 &= 8\\ x_1 &= 1 \end{align}$

2.Schritt: Lineares Gleichungssystem lösen

Setzt du jetzt deine Lösung x_1 = 1 in die ursprüngliche Ebenengleichung ein, kannst du auch Lösungen für x_2 und x_3 finden.

$\begin{align*} \textcolor{violet}{x_1 = 1} \,\text{in}\, F: 6 \cdot \textcolor{violet}{1} + 3 x_2 + x_3 &= 0 \\ 6 + 3x_2 + x_3 &= 0 \end{align*}$

Es gibt nur noch ein kleines Problem: Dein Gleichungssystem enthält drei Variablen ( x_1 , x_2 und x_3 ), aber nur zwei Ebenengleichungen ( und ), die du benutzen kannst, um deine Variablen auszurechnen. Das nennt man auch unterbestimmtes Gleichungssystem und diese Art von Gleichungssystem haben unendlich viele Lösungen. Du kannst dir aber nicht einfach eine der unendlich vielen Lösungen aussuchen und es dabei belassen. Denn jede dieser Lösungen ist ein Punkt der Schnittgerade zweier Ebenen, die du suchst.

Wie findest du also alle Lösungen? Du führst eine neue Variable $\lambda$ ein. Setze $x_3 = \lambda$ , damit du das Gleichungssystem lösen kannst. Später kannst du beliebige Zahlen für $\lambda$ einsetzen und bekommst für jede Zahl eine der unendlichen Lösungen, die einem bestimmten Punkt auf der Schnittgeraden entspricht. Setze also $x_3 = \lambda$ in deine Gleichung ein, um die Lösungen für x_2 zu finden:

$\begin{alignat*}{3} \textcolor{brown}{x_3 = \lambda} \,\text{in}\, F: 6 + 3 x_2 + \textcolor{brown}{\lambda} &= 0 \quad&&|\,-6-\lambda \\ 3x_2 &= - 6 - \lambda &&| \cdot \nicefrac{1}{3}\\ x_2 &= \frac{-6 -\lambda}{3}&& \\ x_2 &= -2 - \frac{1}{3} \cdot \lambda&& \end{alignat*}\begin{align*}\end{align*}$

3.Schritt: Schnittgerade zweier Ebenen aufstellen

Aus den Lösungen für $\textcolor{violet}{x_1}$ , $\textcolor{teal}{x_2}$ und $\textcolor{brown}{x_3}$ kannst du einen Vektor bauen, indem du die drei Lösungen untereinander schreibst. Der Vektor ist die Schnittgerade deiner zwei Ebenen und .

$\begin{gather*} \textcolor{violet}{x_1 = 1} \qquad \textcolor{teal}{x_2 = -2 - \frac{1}{3} \cdot \lambda} \qquad \textcolor{brown}{x_3 = \lambda} \\ g: \begin{pmatrix} \textcolor{violet}{x_1} \\ \textcolor{teal}{x_2} \\ \textcolor{brown}{x_3} \end{pmatrix} = \begin{pmatrix} \textcolor{violet}{1} \\ \textcolor{teal}{-2 - \frac{1}{3} \cdot \lambda} \\ \textcolor{brown}{\lambda} \end{pmatrix} \end{gather}$

Wenn du in seiner Parameterform schreibst, kannst du leicht erkennen, dass tatsächlich eine Gerade ist. Dafür musst du nur die Terme, die $\lambda$ enthalten, und die, welche kein $\lambda$ enthalten, als verschiedene Vektoren schreiben. Das sieht dann so aus:

$\begin{align*} g: \begin{pmatrix} \textcolor{violet}{x_1} \\ \textcolor{teal}{x_2} \\ \textcolor{brown}{x_3} \end{pmatrix} &= \begin{pmatrix} \textcolor{violet}{1 + 0\cdot\lambda} \\ \textcolor{teal}{-2 - \frac{1}{3} \cdot \lambda} \\ \textcolor{brown}{0 + \lambda} \end{pmatrix} \\ \end{align*}$

Schreibe den Vektor als Summe aus einem Vektor ohne $\lambda$ und einen Vektor mit $\lambda$ .

$\begin{align*} g: \begin{pmatrix} \textcolor{violet}{x_1} \\ \textcolor{teal}{x_2} \\ \textcolor{brown}{x_3} \end{pmatrix} &= \begin{pmatrix} \textcolor{violet}{1} \\ \textcolor{teal}{-2} \\ \textcolor{brown}{0} \end{pmatrix} + \begin{pmatrix} \textcolor{violet}{0\cdot\lambda} \\ \textcolor{teal}{-\frac{1}{3} \cdot \lambda} \\ \textcolor{brown}{\lambda} \end{pmatrix} \\ \end{align*}$

Klammere $\lambda$ aus und schreibe es vor den Vektor.

$\begin{align*} g: \begin{pmatrix} \textcolor{violet}{x_1} \\ \textcolor{teal}{x_2} \\ \textcolor{brown}{x_3} \end{pmatrix} &= \begin{pmatrix} \textcolor{violet}{1} \\ \textcolor{teal}{-2} \\ \textcolor{brown}{0} \end{pmatrix} + \lambda \begin{pmatrix} \textcolor{violet}{0} \\ \textcolor{teal}{-\frac{1}{3}} \\ \textcolor{brown}{1} \end{pmatrix} \end{align*}$

Und voilà! Du hast die Schnittgerade zweier Ebenen und gefunden. Damit hast du gezeigt, dass sich die beiden Ebenen schneiden. Und du weißt genau, wo sie sich schneiden: Die Ebenen schneiden sich entlang der Schnittgeraden . Alle Punkte, die auf dieser Geraden liegen, sind sowohl ein Teil von als auch von .

Quiz zum Thema Schnittgerade zweier Ebenen

Abstand Gerade-Gerade

Schnittgeraden findest du jetzt wie ein Weltmeister, aber weißt du schon wie du den Abstand von zwei Geraden findest? Schau dir direkt unseren Beitrag dazu an!

Zum Video: Abstand Gerade Gerade

zur Videoseite: Schnittgerade zweier Ebenen

Beliebte Inhalte aus dem Bereich Geometrie

Koordinatenform

Hessesche Normalform

Ebenengleichung

Schnittgerade zweier Ebenen

Schnittpunkt Gerade Ebene

Koordinatenform in Parameterform

Parameterform in Koordinatenform

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .