Umfang Dreieck
Du fragst dich: Wie berechnet man den Umfang eines Dreiecks? Hier erklären wir dir genau, wie du den Umfang von Dreiecken bestimmen kannst! Sieh dir auch unser Video dazu an!
Inhaltsübersicht
Umfang Dreieck berechnen
Sehen wir uns die Berechnung des Umfangs an einem Beispiel an. Du hast ein Dreieck mit den Seiten a = 4 cm, b = 6 cm und c = 5 cm.
Um den Umfang zu berechnen, nutzt du die obige Formel:
U = a + b + c
Du setzt die Längen der Seiten in die Formel ein: Für a setzt du 4 cm, für b 6 cm und für c 5 cm ein.

Mit den Längen von a, b und c kannst du den Umfang direkt ausrechnen, indem du sie addierst:
![Rendered by QuickLaTeX.com \[U=15 \; \textnormal{cm}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-9d4c09faedc118e1aecdb82a6fd8a011_l3.png)
Der Umfang des Dreiecks beträgt 15 cm. Du weißt nun, wie du den Umfang eines Dreieck berechnen kannst!
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Umfang berechnen bei verschiedenen Einheiten
Du fragst dich, wie groß der Umfang eines Dreiecks ist. Du weißt, dass Seite a 37 cm lang ist und Seite b 62 cm lang ist. Die Seitenlänge von c beträgt 1,2 m. Wie berechnest du den Umfang des Dreiecks?
Als Erstes nimmst du dir die Umfang Formel zur Hand.
U = a + b + c
Du möchtest die Längenangaben deiner Seiten einsetzen. Allerdings sind die Längen von a und b in Zentimeter und die Länge von c in Meter angegeben. Um alle Längen zusammenzählen zu können, benötigst du sie in derselben Einheit. Daher wandelst du die Länge der Seite c in cm um.
![Rendered by QuickLaTeX.com \[ 1,2 \; \textnormal{m} = 120 \; \textnormal{cm}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-d3bdc32151401dfbdbe901d129301c29_l3.png)
Die Seite c ist also 120 cm lang.
Jetzt kannst du alle Seitenlängen in die Formel einsetzen und zusammenzählen:

Spitze, du hast herausgefunden, dass der Umfang des Dreiecks 219 cm beträgt.
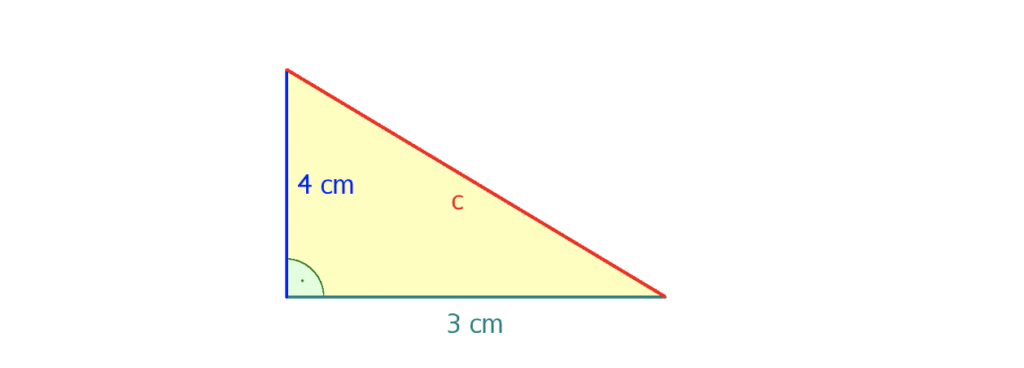
Umfang rechtwinkliges Dreieck berechnen
Du möchtest den Umfang von diesem rechtwinkligen Dreieck berechnen. Du weißt, dass die Seite a 4 cm lang ist und die Seite b 3 cm lang ist.
![Rendered by QuickLaTeX.com \[U=\textcolor{blue}{4 \; \textnormal{cm}} + \textcolor{olive}{3 \; \textnormal{cm}} + \textcolor{red}{c}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-d50956e9fb4e9703ce4288823821bcd1_l3.png)
Wie kannst du nun dem Umfang berechnen? Um den Umfang berechnen zu können, benötigst du noch die Länge von c. Um die Länge der Seite c herauszufinden, führst du zunächst eine Dreiecksberechnung durch.
Die Seitenlängen a und b kennst du bereits. Du weißt, dass das Dreieck einen rechten Winkel hat. Deshalb kannst du mithilfe des Satzes des Pythagoras die Länge von c berechnen.
![Rendered by QuickLaTeX.com \[a^2 + b^2 =c^2\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-7c6935a1a38920c803262e9122eec1b4_l3.png)
Dafür setzt du die Längenangaben von a und b in den Satz des Pythagoras ein. Anschließend löst du nach c auf.

Du hast herausgefunden, dass die Seite c 5 cm lang ist.
Jetzt kennst du die Längen aller Seiten. Den Umfang des Dreiecks kannst du berechnen, indem du alle Längenangaben in die Formel einsetzt.
![Rendered by QuickLaTeX.com \[U=\textcolor{blue}{4 \; \textnormal{cm}} + \textcolor{olive}{3 \; \textnormal{cm}} + \textcolor{red}{5 \; \textnormal{cm}}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-e6baee234dce459364df170cdf5289f1_l3.png)
![Rendered by QuickLaTeX.com \[U=12 \; \textnormal{cm}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-2ecc44ebdb06deb479f2752d212721f8_l3.png)
Du hast herausgefunden, dass der Umfang deines Dreiecks 12 cm beträgt. Super, die Berechnung des Umfangs von Dreiecken beherrschst du nun bestens!
Umfang Dreieck — häufigste Fragen
(ausklappen)
Umfang Dreieck — häufigste Fragen
(ausklappen)-
Was bedeutet der Umfang bei einem Dreieck?Der Umfang eines Dreiecks bedeutet die gesamte Länge seines Randes, also die Summe aller drei Seitenlängen. Dafür werden die Seiten
 ,
,  und
und  zusammengezählt. Mathematisch schreibt man das als
zusammengezählt. Mathematisch schreibt man das als  .
.
-
Wie berechne ich den Umfang eines Dreiecks mit drei Seitenlängen?Den Umfang eines Dreiecks mit drei bekannten Seitenlängen berechnest du, indem du alle drei Seiten addierst:
 . Zum Beispiel ergibt sich bei
. Zum Beispiel ergibt sich bei  ,
,  und
und  der Umfang
der Umfang  .
.
-
Wann muss ich beim Umfang zuerst die Einheiten umrechnen?Beim Umfang musst du die Einheiten zuerst umrechnen, wenn die Seitenlängen in unterschiedlichen Einheiten angegeben sind, weil du nur gleichartige Einheiten addieren kannst. Zum Beispiel werden Meter in Zentimeter umgerechnet, wenn zwei Seiten in cm und eine Seite in m gegeben ist.
-
Wie rechne ich Meter in Zentimeter um, bevor ich addiere?Meter rechnest du in Zentimeter um, indem du die Meterangabe in eine Zentimeterangabe umwandelst, sodass alle Seiten dieselbe Einheit haben. Konkret:
 . Danach kannst du die Seitenlängen in cm in
. Danach kannst du die Seitenlängen in cm in  addieren.
addieren.
-
Wie finde ich die fehlende Seite im rechtwinkligen Dreieck für den Umfang?Die fehlende Seite im rechtwinkligen Dreieck findest du mit dem Satz des Pythagoras, damit du danach den Umfang addieren kannst. Es gilt
 , anschließend wird nach
, anschließend wird nach  aufgelöst. Beispiel:
aufgelöst. Beispiel:  ergibt
ergibt  .
.
Flächeninhalt Dreieck
Nun fragst du dich sicher, wie du die Fläche eines Dreiecks berechnen kannst. Um zu erfahren, wie du den Flächeninhalt eines Dreiecks herausfinden kannst, schaust du dir am besten unseren Beitrag dazu an. Hier kommst du zum Video . Bis gleich!