Flächenberechnung
Hier und im Video erfährst du alles über die Flächenberechnung und wie du mit der richtigen Formel jeden Flächeninhalt berechnen kannst!
Inhaltsübersicht
Flächenberechnung einfach erklärt
Wenn du einen Flächeninhalt A einer Figur (Quadrat, Rechteck, Dreieck, Kreis) berechnen möchtest, brauchst du die passende Formel.
Hier findest du die wichtigsten Formeln, um einen Flächeninhalt zu berechnen:
| Figur | Flächeninhalt Formel |
| A = a · a = a2 | |
| Rechteck | A = a · b |
| Dreieck | A = 0,5 · a · ha |
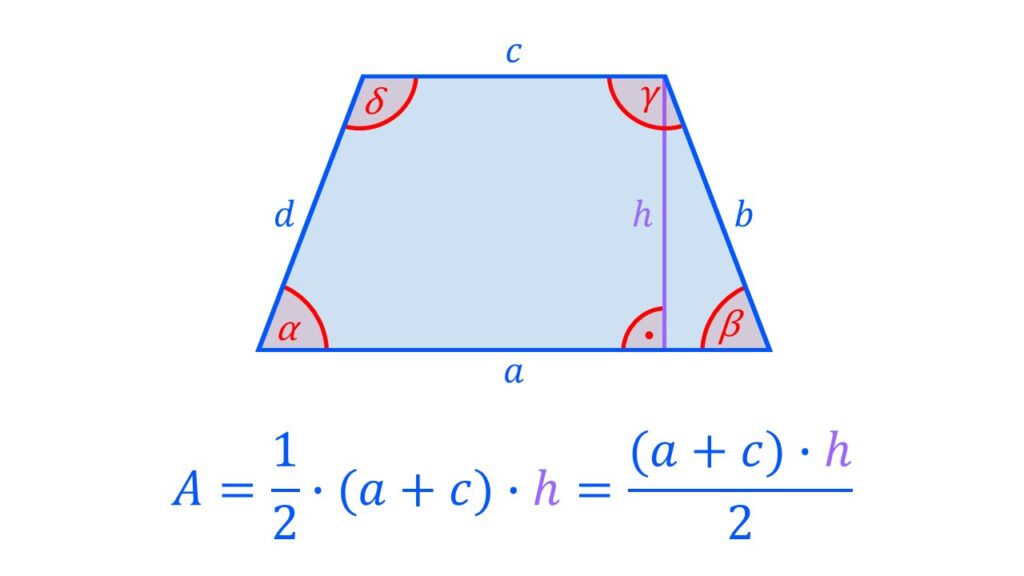
| Trapez | A = 0,5 · (c + a) · h |
| Parallelogramm | A = a · ha |
| Raute | A = a · ha oder A = 0,5 · e · f |
| Drachenviereck | A = 0,5 · e · f |
| Kreis | A = π · r2 |
Übrigens: Neben dem Flächeninhalt kannst du auch die Länge des Randes einer Fläche berechnen. Du berechnest den sogenannten Umfang, indem du die Länge aller Seiten zusammenzählst.
Flächenberechnung Rechteck
Beim Rechteck sind die gegenüberliegenden Seiten gleich lang (a = c und b = d) und parallel (a ‖ c und b ‖ d).
Flächeninhalt Rechteck Formel: A = a · b
Winkel: α = β = γ = δ = 90°
Winkelsumme: α + β + γ + δ = 360°
Flächenberechnung Dreieck
Ein Dreieck hat immer drei Seiten und drei Winkel.
Flächeninhalt Dreieck Formel: 
Winkelsumme: α + β + γ = 180°
Es gibt neben dem allgemeinen Dreieck drei besondere Dreiecksarten. Sie haben jeweils eine besondere Formel für die Fläche:
-
Gleichschenkliges Dreieck — Zwei Seiten sind gleich lang.
Fläche:
-
Gleichseitiges Dreieck — Alle drei Seiten sind gleich lang.
Fläche:
-
Rechtwinkliges Dreieck — Ein Winkel beträgt 90°.
Fläche:
Flächenberechnung Parallelogramm
Das Parallelogramm ist ein Viereck, bei dem die zwei gegenüberliegenden Seiten parallel (a ‖ c und b ‖ d) und gleich lang (a = c und b = d) sind.
Flächeninhalt Parallelogramm Formel: A = a · ha
Winkel:
α = γ
β = δ
Winkelsumme: α + β + γ + δ = 360°
Flächenberechnung Raute
Die Raute ist ein Parallelogramm, bei dem alle vier Seiten gleich lang (a = b = c = d) und gegenüberliegende Seiten parallel (a ‖ c und b ‖ d) sind.
Um den Flächeninhalt auszurechnen, hast du zwei Möglichkeiten:
Formel mit Höhe: A = a · ha
Formel mit Diagonalen: 
Winkel:
α = γ
β = δ
Winkelsumme: α + β + γ + δ= 360°
Flächenberechnung Drachenviereck
Das Drachenviereck hat zwei Diagonalen e und f, die im rechten Winkel zueinander stehen. Die zwei benachbarten Seiten (a = b) und (c = d) sind gleich lang.
Flächeninhalt Drachenviereck Formel:
Winkel:
α = γ
β = δ
Winkelsumme: α + β + γ + δ= 360°
Flächenberechnung Kreis
Den Flächeninhalt von einem Kreis kannst du mit seinem Radius r und der Kreiszahl π berechnen.
Flächeninhalt Kreis Formel: A = π · r2
Bei einem Kreis sind alle Punkte auf der Kreislinie gleich weit vom Mittelpunkt M entfernt. Dieser Abstand ist der Radius r. Der Durchmesser d ist der größtmögliche Abstand zwischen zwei Punkten auf der Kreislinie.
Merke: Der Durchmesser ist immer zweimal so groß wie der Radius!
Es gilt:
d = 2 • r
r = 0,5 • d
Zusammengesetzte Flächen berechnen
Wenn du mehrere Flächen miteinander kombinierst, erhältst du eine zusammengesetzte Fläche. Aber wie kannst du ihren Flächeninhalt berechnen?
1. Zusammengesetzte Fläche in ihre einzelnen Figuren zerlegen:
Der untere Teil der Figur ist ein Rechteck und der obere ein rechtwinkliges Dreieck.
2. Flächeninhalt des Rechtecks berechnen:
Für den Flächeninhalt des Rechtecks gilt:
ARechteck = a • b
In der Abbildung kannst du erkennen, dass dein Rechteck 8 cm lang ist. Die Breite kennst du nicht. Allerdings kennst du die Gesamtlänge der Figur und die Breite des Dreiecks.
Die Breite des Rechtecks erhältst du durch die Rechnung: b = 6 cm – 2 cm = 4 cm. Jetzt musst du nur noch in die Formel einsetzen.
ARechteck = 8 cm • 4 cm = 32 cm²
3. Flächeninhalt des rechtwinkligen Dreiecks berechnen:
Für den Flächeninhalt eines rechtwinkligen Dreiecks gilt:
ADreieck = 0,5 • a • b
Die Seitenlängen a = 2 cm und b = 8 cm kannst du aus der Abbildung ablesen.
ADreieck = 0,5 • 2 cm • 8 cm
ADreieck = 0,5 • 16 cm² = 8 cm²
4. Beide Flächeninhalte addieren:
Agesamt = 32 cm² + 8 cm² = 40 cm²
Der Flächeninhalt der zusammengesetzten Form beträgt 40 cm².
Flächenberechnung — häufigste Fragen
-
Was ist der Flächeninhalt und mit welcher Formel wird er für ein Rechteck berechnet? Der Flächeninhalt gibt an, wie groß eine zweidimensionale Fläche ist. Er wird in Quadrat-Einheiten gemessen, z. B. Quadratmeter (m2) oder Quadratzentimeter (cm2).
Für ein Rechteck mit den Seitenlängen a und b berechnest du den Flächeninhalt mit der Formel: A = a • b
-
Mit welchen Formeln kann man Flächen berechnen? Fläche Formel Quadrat A = a · a = a2 Rechteck A = a · b Dreieck A = 0,5 · c · hc Parallelogramm A = a · ha Kreis A = π · r2
Flächeneinheiten
Bei der Flächenberechnung musst du häufig auch Flächeneinheiten umrechnen. Wie das geht, erfährst du hier in unserem Video!
