Umfang Rechteck
Du fragst dich, was es mit dem Umfang eines Rechtecks auf sich hat? In diesem Beitrag und Video erklären wir dir, was ein Rechteck ist und wie du seinen Umfang berechnest!
Inhaltsübersicht
Umfang Rechteck einfach erklärt
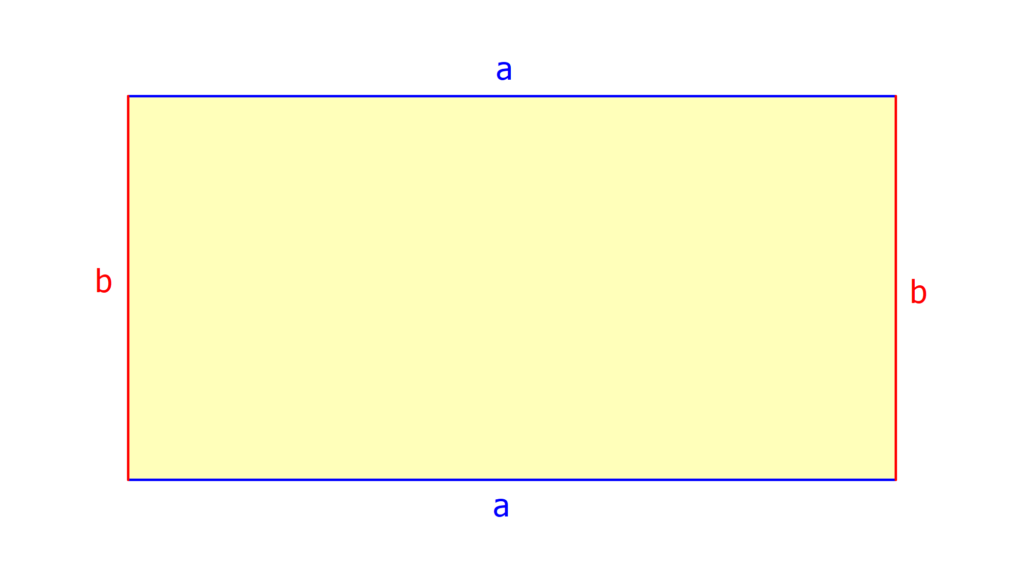
Ein Rechteck ist eine geometrische Figur und gehört zu den Vierecken . Es hat vier rechte Winkel (90°) und die gegenüberliegenden Seiten sind parallel und gleich lang.
Was ist der Umfang eines Rechtecks? Du gibst damit an, welche Strecke du laufen musst, um einmal das Rechteck abzulaufen. Der Umfang sagt dir also, wie lang der gesamte Rand des Rechtecks ist.
Um den Rechteck Umfang U zu berechnen, addierst du alle 4 Seiten miteinander. U = a + b + a + b . Du zählst zweimal die Länge a und zweimal die Breite b zusammen.
Um den Rechteck Umfang zu berechnen, addierst du die Längen aller Seiten miteinander. Die Umfang Formel ist also U = 2 · a + 2 · b.
Schau dir die Berechnung des Rechteck Umfangs direkt an einem Beispiel an.
Umfang berechnen Rechteck – Beispiel 1
Lass uns den Umfang berechnen von einem Rechteck mit Seitenlänge a = 10 cm und b = 0,05 m.
Achtung! Um die Umfang Formel benutzen zu können, brauchst du eine gemeinsame Längeneinheit. Wandle 0,05 m also in Zentimeter um. Hier zeigen wir dir, wie das geht.
0,05 m · 100 = 5 cm
Nun kannst du Schritt für Schritt vorgehen:
- Formel aufstellen: Zuerst notierst du dir die Formel für den Umfang im Rechteck.
U = 2 · a + 2 · b
- Angaben einsetzen: Jetzt kannst du die Zahlenwerte einsetzen, die für a und b gegeben sind.
U = 2 · 10 cm + 2 · 5 cm
- Ergebnis berechnen: Zum Schluss musst du nur noch die eigentliche Rechnung durchführen und alle Zahlen zusammenfassen.
U = 20 cm + 10 cm = 30 cm
Der Umfang von diesem Rechteck beträgt also 30 cm.
Umfang berechnen Rechteck – Beispiel 2
Die Formel für den Rechteck Umfang kannst du auch zu U = 2 · (a + b) zusammenfassen, indem du die 2 ausklammerst. Bei der Berechnung kannst du einfach genauso vorgehen.
Berechne den Umfang vom Rechteck mit den Seitenlängen a = 2 cm und b = 8 cm.
- Formel aufstellen:
U = 2 · (a + b)
- Angaben einsetzen:
U = 2 · (2 cm + 8 cm)
- Ergebnis berechnen:
U = 2 · 10 cm = 20 cm
Der Rechteck Umfang ist 20 cm groß.
Umfang berechnen Rechteck – Formel umstellen
Manchmal ist der Umfang vom Rechteck gegeben und du musst daraus eine Seitenlänge berechnen. Auch das funktioniert in wenigen Schritten mit der Formel für den Umfang im Rechteck.
Gegeben ist der Umfang vom Rechteck U = 20 cm und die Seite b = 6 cm. Wie lang ist die Seite a?
- Formel aufstellen: Zuerst brauchst du die allgemeine Umfang Formel. Wir benutzen diesmal die Variante ohne Klammern.
U = 2 · a + 2 · b
- Formel umstellen: Jetzt stellst du die Formel so um, dass du damit die Seitenlänge a berechnen kannst.
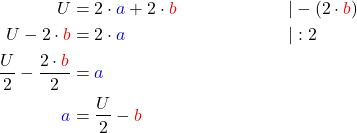
- Angaben einsetzen: Im nächsten Schritt setzt du die gegebenen Zahlenwerte ein. Diesmal ist das der Umfang und die Seitenlänge b.

- Ergebnis berechnen: Abschließend musst du nur noch das Ergebnis ausrechnen.
a = 10 cm – 6 cm = 4 cm
Die Seitenlänge a ist 4 cm lang.
Umfang Rechteck – Anwendungsbeispiel 1
Oft begegnet dir der Rechteck Umfang in einer Textaufgabe. Schau dir deshalb ein paar Anwendungsbeispiele an:
An deiner Schule wurde ein Gemüsebeet angelegt. Dieses Beet hat die Form eines Rechtecks und ist fünf Meter lang und drei Meter breit. Es soll durch einen Zaun geschützt werden. Wie lang muss der Zaun insgesamt sein?
Die Antwort auf diese Frage findest du mit dem Umfang vom Rechteck.
- Formel aufstellen:
U = 2 · (a + b)
- Angaben einsetzen:
U = 2 · (5 m + 3 m)
- Ergebnis berechnen:
U = 2 · 8 m = 16 m
Der Zaun wird insgesamt 16 Meter lang sein.
Umfang Rechteck – Anwendungsbeispiel 2
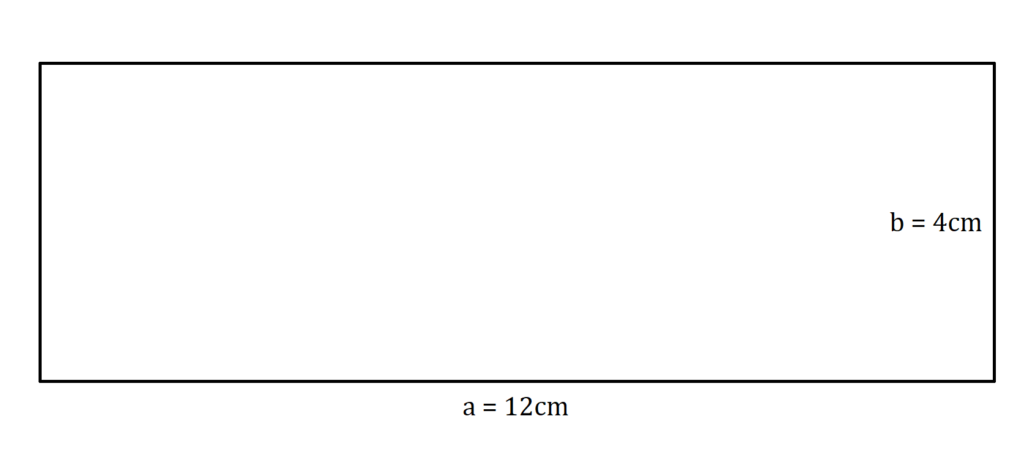
Ken hat eine Brotzeitdose, die aussieht wie ein Rechteck. Sie ist 12 cm breit und 4 cm hoch. Weil er lange unterwegs sein wird, möchte er den Deckel gerne zusätzlich mit etwas Klebeband befestigen. Berechne die Länge des Klebestreifens, den Ken dafür benötigt.
Lösung:
Der Klebestreifen muss genauso lang sein wie der Umfang vom Rechteck. Du musst also nur die Umfang Formel anwenden.
U = 2 · (a + b) = 2 · (12 cm + 4 cm) = 2 · 16 cm = 32 cm
Ken braucht einen Klebestreifen, der 32 cm lang ist.
Umfang Rechteck — häufigste Fragen
-
Wie berechnet man den Umfang eines Rechtecks?
Um den Umfang eines Rechtecks zu bestimmen, rechnest du einfach die Länge aller vier Seiten zusammen. Da die gegenüberliegenden Seiten eines Rechtecks aber immer gleich lang sind, kannst du das abkürzen: U = 2 • a + 2 • b.
-
Wie ist die Umfang Rechteck Formel?
Die Formel für den Umfang eines Rechtecks lautet U = 2 • a + 2 • b. Das heißt, du rechnest jeweils die Länge der Seite a und der Seite b mal 2. Beides addierst du dann und erhältst den Umfang.
Parallelogramm – Flächeninhalt und Umfang
Das Rechteck ist eine besondere Form des Parallelogramms. Wie du Flächeninhalt und Umfang eines Parallelogramms berechnest, erfährst du in diesem Video!