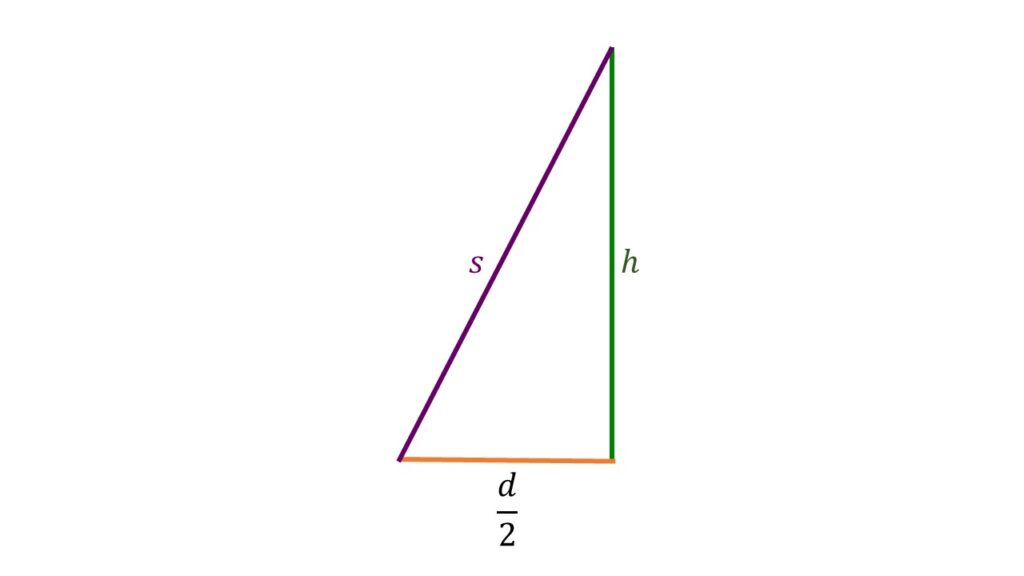Video

Quiz

Hier geht's zum Video „Quadrat“

Hier geht's zum Video „Volumen Pyramide“

Hier geht's zum Video „Flächeninhalt Quadrat“

Hier geht's zum Video „Mediendesigner/in“

Hier geht's zum Video „Volumen Kegel“

Pyramide

Wichtige Inhalte in diesem Video

Was ist eine Pyramide?

Sonderformen der Pyramide

Volumen Pyramide

Oberfläche Pyramide

Was ist eine Pyramide und welche Arten von Pyramiden gibt es in Mathe? Die Antworten auf deine Fragen bekommst du hier und in unserem Video !

Inhaltsübersicht

Was ist eine Pyramide?

im Videozur Stelle im Video springen

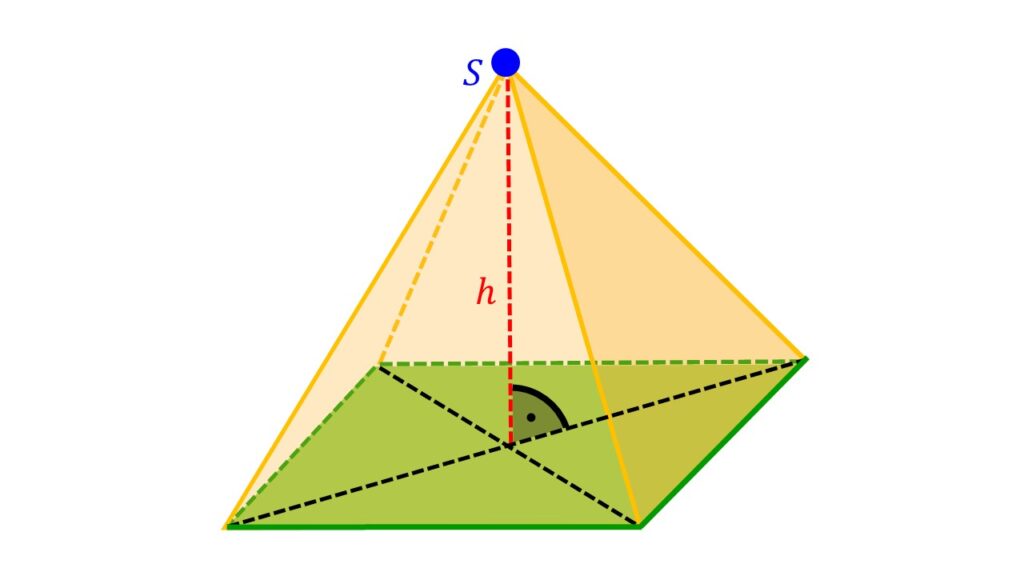
Eine Pyramide in Mathe ist ein geometrischer Körper . Er hat eine Spitze S und als Grundfläche G ein beliebiges Vieleck, zum Beispiel ein Dreieck , Viereck oder Fünfeck. Die Seitenflächen haben die Form von Dreiecken.

Pyramide Geometrie, Mantelfläche Pyramide, Pyramide Mathe, Pyramiden Körper, Pyramide Körper, Mathe Pyramide, gerade Pyramide, Höhe Pyramide, Pyramide Mathematik, Pyramide Eigenschaften, Geometrie Pyramide, Viereckspyramide, eine Pyramide, Wie viele Ecken hat eine Pyramide, Wie viele Kanten hat eine Pyramide, Pyramide im Alltag, Wie viele Flächen hat eine Pyramide — Pyramide

Den Abstand von der Spitze S zur Grundfläche G ist die Höhe h. Die Kanten der Grundflächen heißen Grundkanten und die Kanten der Seitenflächen nennst du Seitenkanten.

Rechnest du alle Seitenflächen zusammen, bekommst du die Mantelfläche M der Pyramide .

Sonderformen der Pyramide

im Videozur Stelle im Video springen

In der Geometrie gibt es verschiedene Formen der Pyramide. Welche das sind und was für Eigenschaften sie haben, siehst du hier:

Gerade Pyramide

Die gerade Pyramide hat folgende Eigenschaften:

Alle Kanten der Mantelfläche sind gleich lang.
Die Spitze S liegt senkrecht über dem Mittelpunkt M.

Pyramide Geometrie, Mantelfläche Pyramide, Pyramide Mathe, Pyramiden Körper, Pyramide Körper, Mathe Pyramide, gerade Pyramide, Höhe Pyramide, Pyramide Mathematik, Pyramide Eigenschaften, Geometrie Pyramide, Viereckspyramide, eine Pyramide — Gerade Pyramide

Regelmäßige/reguläre Pyramide

Bei einer regelmäßigen Pyramide ist

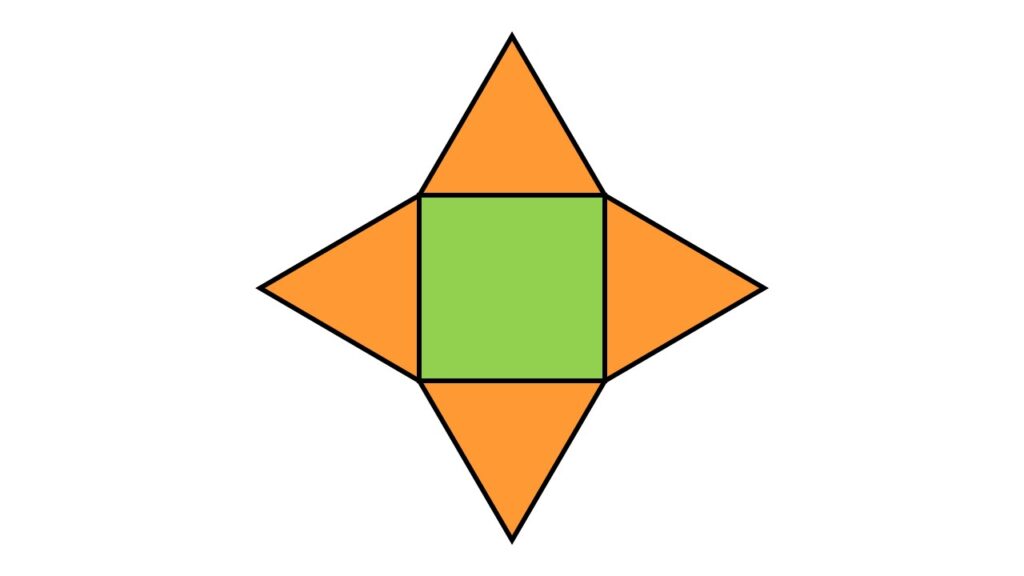
die Grundfläche ein regelmäßiges Vieleck . Also ein Vieleck mit gleich langen Seiten und gleich großen Winkeln. Hier ist das ein Quadrat .
die Spitze S senkrecht über der Mittelpunkt M.

Pyramide Geometrie, Mantelfläche Pyramide, Pyramide Mathe, Pyramiden Körper, Pyramide Körper, Mathe Pyramide, gerade Pyramide, Höhe Pyramide, Pyramide Mathematik, Pyramide Eigenschaften, Geometrie Pyramide, Viereckspyramide, eine Pyramide, regelmäßige Pyramide, reguläre Pyramide — Regelmäßige Pyramide

Schiefe Pyramide

Bei einer schiefen Pyramide

liegt die Spitze S nicht senkrecht über dem Mittelpunkt M.
ist das Volumen genauso groß wie bei einer geraden Pyramide mit derselben Höhe h.

Pyramide Geometrie, Mantelfläche Pyramide, Pyramide Mathe, Pyramiden Körper, Pyramide Körper, Mathe Pyramide, gerade Pyramide, Höhe Pyramide, Pyramide Mathematik, Pyramide Eigenschaften, Geometrie Pyramide, Viereckspyramide, eine Pyramide, schiefe Pyramide — Schiefe Pyramide

Reguläres Tetraeder

Ein reguläres Tetraeder hat

vier gleichseitige Dreiecke als Flächen.
sechs gleich lange Kanten.
eine Spitze S, die senkrecht über dem Mittelpunkt M liegt.

Pyramide Geometrie, Mantelfläche Pyramide, Pyramide Mathe, Pyramiden Körper, Pyramide Körper, Mathe Pyramide, gerade Pyramide, Höhe Pyramide, Pyramide Mathematik, Pyramide Eigenschaften, Geometrie Pyramide, Viereckspyramide, eine Pyramide, regulärer Tetraeder — Reguläres Tetraeder

Super! Jetzt kennst du die verschiedenen Formen der Pyramide. Bei einer Pyramide in der Geometrie gibt es auch einige Größen, die du berechnen kannst. Welche Formeln es dafür gibt, siehst du als Nächstes!

Volumen Pyramide

im Videozur Stelle im Video springen

Das Innere einer Pyramide, also das Volumen V kannst du mit der Grundfläche und der Höhe ganz einfach berechnen. Du benutzt dafür die Formel

V_Pyramide = ⅓ · G · h

Achte darauf, dass die Grundfläche unterschiedliche Formen haben kann. Um sie richtig zu berechnen, benutzt du die dazu passende Formel.

Beispiel: Berechne das Volumen einer quadratischen Pyramide mit der Seitenlänge a = 4 cm und der Höhe h = 8 cm.

Pyramide Geometrie, Mantelfläche Pyramide, Pyramide Mathe, Pyramiden Körper, Pyramide Körper, Mathe Pyramide, gerade Pyramide, Höhe Pyramide, Pyramide Mathematik, Pyramide Eigenschaften, Geometrie Pyramide, Viereckspyramide, eine Pyramide, Volumen Pyramide berechnen — Volumen Pyramide

Die Grundfläche ist ein Quadrat, also berechnest du sie mit der Formel für den Quadrat Flächeninhalt G = a · a.

Ersetze das G durch die Quadrat Formel und setze deine Werte ein:

V_Pyramide = ⅓ · a · a · h

V_Pyramide = ⅓ · 4 cm · 4 cm · 8 cm

V_Pyramide ≈ 42,7 cm³

Das Volumen ist 42,7 cm³ groß.

Hat die Pyramide eine andere Grundfläche, benutzt du andere Formeln. Hier siehst du, welche das sind:

Quadrat: G = a · a
Dreieck: G = ½ · g · h_G(g = Grundkante, h_G = Höhe des Dreiecks)
Rechteck: G = a · b

Oberfläche Pyramide

im Videozur Stelle im Video springen

Die Oberfläche einer Pyramide ist das Äußere, das du berühren kannst. Du berechnest sie, indem du die Grundfläche G mit der Mantelfläche M der Pyramide addierst.

O_Pyramide = G + M

Die Grundfläche und die Mantelfläche können unterschiedliche Formen haben. Schau dir zum Beispiel eine reguläre Pyramide an.

Pyramide Geometrie, Mantelfläche Pyramide, Pyramide Mathe, Pyramiden Körper, Pyramide Körper, Mathe Pyramide, gerade Pyramide, Höhe Pyramide, Pyramide Mathematik, Pyramide Eigenschaften, Geometrie Pyramide, Viereckspyramide, eine Pyramide, Oberfläche Pyramide, Netz einer regulären Pyramide, Pyramide Netz — Netz einer regulären Pyramide

Weil die Grundfläche ein Quadrat ist und die vier Seitenflächen gleichseitige Dreiecke sind, bekommst du diese Formel:

O_Pyramide = a · a + 4 · $\textcolor{orange}{\frac{a \cdot h_a}{2}}$

Pyramide berechnen

Bei einer geraden Pyramide mit quadratischer Grundfläche kannst du außerdem noch die Diagonale d, die Höhe h_a und die Seitenkanten berechnen. Wie das geht, siehst du hier:

Diagonale d

Die Diagonale der Grundfläche berechnest du mit dem Satz des Pythagoras :

Diagonale der Pyramide, Pyramide Geometrie, Pyramide Mathematik — Diagonale im Quadrat

Du bekommst die Formel:

d² = a² + a²

d² = 2 · a²

d = $\sqrt{2}$ · a

Seitenfläche

Bei der Seitenfläche kannst du die Höhe h_a berechnen. Hier siehst du, wie das geht:

Höhe h_a

Die Höhe h_a ist die längste Seite der Seitenfläche.

Pyramide Geometrie, Mantelfläche Pyramide, Pyramide Mathe, Pyramiden Körper, Pyramide Körper, Mathe Pyramide, gerade Pyramide, Höhe Pyramide, Pyramide Mathematik, Pyramide Eigenschaften, Geometrie Pyramide, Viereckspyramide, Höhe Pyramide, Höhe ha — Höhe h_a eines Dreiecks

Du berechnest sie mit dem Pythagoras:

h_a² = ( $\frac{a}{2}$ )² + h²

h_a = $\sqrt{(\frac{a}{2})+h^2}$

Die Seitenfläche einer Pyramide kannst du auf zwei Wegen berechnen:

1. Mit der Höhe h_a

Um die Seitenkante s mit der Höhe h_a zu berechnen, benutzt du den Satz des Pythagoras.

Pyramide Geometrie, Mantelfläche Pyramide, Pyramide Mathe, Pyramiden Körper, Pyramide Körper, Mathe Pyramide, gerade Pyramide, Höhe Pyramide, Pyramide Mathematik, Pyramide Eigenschaften, Geometrie Pyramide, Viereckspyramide, eine Pyramide, Seitenkante Pyramide — Seitenkante s im Dreieck

Du rechnest:

s² = ( $\frac{a}{2}$ )² + h²

s = $\sqrt{(\frac{a}{2})+h^2}$

2. Mit der Höhe h

Die Seitenkante s kannst du auch mit der allgemeinen Höhe h berechnen.

Seitenkante s im Dreieck, Pyramide Geometrie, Mantelfläche Pyramide, Pyramide Mathe, Pyramiden Körper, Pyramide Körper, Mathe Pyramide, gerade Pyramide, Höhe Pyramide, Pyramide Mathematik, Pyramide Eigenschaften, Geometrie Pyramide, Viereckspyramide, eine Pyramide, Seitenkante im Dreieck — Seitenkante s im Dreieck

Du benutzt dafür auch den Pythagoras:

s² = ( $\frac{d}{2}$ )² + h²

s = $\sqrt{(\frac{d}{2})+h^2}$

Quiz zum Thema Pyramide

Kegel

Es gibt noch andere geometrische Körper , die du dir unbedingt anschauen solltest. Hier stellen wir dir den Kegel vor.

Zum Video: Volumen Kegel

zur Videoseite: Pyramide

Beliebte Inhalte aus dem Bereich Geometrie

Oberfläche Pyramide

Mantelfläche Pyramide

Volumen Pyramide

Pyramidenstumpf

Tetraeder - Volumen und Oberfläche

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .