Pyramidenstumpf
Was ist ein Pyramidenstumpf und wie berechnest du sein Volumen? Die Antworten auf deine Fragen bekommst du hier und in unserem Video !
Inhaltsübersicht
Pyramidenstumpf einfach erklärt
Der Pyramidenstumpf ist ein geometrischer Körper . Er sieht aus wie eine Pyramide , bei der die Spitze abgeschnitten wurde.
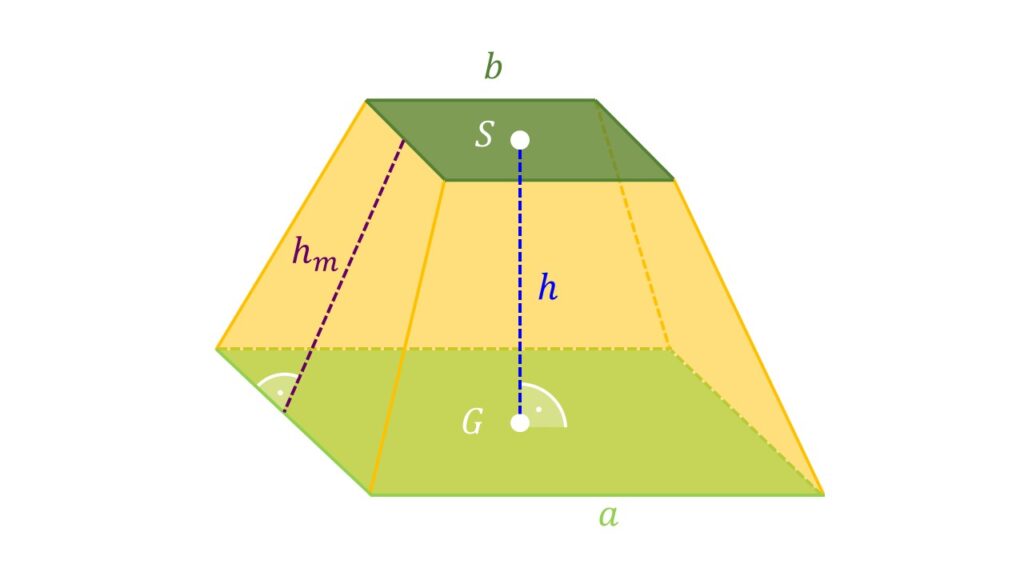
Ein Pyramidenstumpf hat eine quadratische Grundfläche mit den Seitenlängen a und eine quadratische Schnittfläche mit den Seitenlängen b. Seine Seitenflächen haben die Form von gleichschenkligen Trapezen . Gemeinsam bilden die vier Seitenflächen die Mantelfläche M.
Den Abstand von der Grundfläche bis zur Schnittfläche nennst du Höhe h des Stumpfes. Eine andere Höhe im Pyramidenstumpf ist die Höhe der Mantelfläche. Du nennst sie Höhe hm.
Du kannst den Pyramidenstumpf auch berechnen. Wie das geht, siehst du jetzt!
Pyramidenstumpf Volumen
Das Volumen V beschreibt den Rauminhalt, also das Innere eines Körpers. Es sagt dir zum Beispiel, wie viel Luft in den Pyramidenstumpf passt. Doch wie lautet die Formel zur Berechnung des Volumens eines Pyramidenstumpfes?
Um das Volumen des Pyramidenstumpfs zu berechnen, benutzt du die Formel
VPyramidenstumpf =  · (a2 + a · b + b2)
· (a2 + a · b + b2)
Beispiel: Berechne das Volumen des Pyramidenstumpfes mit den Längen a = 8 cm, b = 4 cm und der Höhe h = 3 cm.
Lösung: Setze die Werte in die Pyramidenstumpf Formel ein und rechne aus. Du erhältst
VPyramidenstumpf =  · ((8 cm)2 + 8 cm · 4 cm + (4 cm)2)
· ((8 cm)2 + 8 cm · 4 cm + (4 cm)2)
VPyramidenstumpf = 112 cm3
Auch die Flächen des Pyramidenstumpfs kannst du berechnen. Schau dir an, wie das geht!
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Pyramidenstumpf berechnen
Jetzt erfährst du, wie du die Grund– und die Schnittfläche, die Mantelfläche und die gesamte Oberfläche des Pyramidenstumpfes berechnest!
Grund- und Schnittfläche
Die obere und die untere Fläche im Pyramidenstumpf kannst du ganz einfach berechnen, denn sie haben die Form von Quadraten . Du rechnest Seitenlänge mal Seitenlänge.
Die Pyramidenstumpf Formeln für die Grund- und Schnittfläche sind also
G = a · a
S = b · b
Mantelfläche
Die Mantelfläche M besteht aus den vier gleichschenkligen Trapezen. Die Fläche A eines Trapezes berechnest du mit der Formel
ATrapez = ½ · (a + b) · h
Die Seiten a und b sind die Längen der Grund- und der Schnittfläche. Die Höhe ist in diesem Fall die Höhe hm der Mantelfläche. Weil die Mantelfläche aus 4 Trapezen besteht, rechnest du die Fläche noch mal 4. Dadurch bekommst du die Pyramidenstumpf Formel für die Mantelfläche
M = 4 · ½ · (a + b) · hm → M = 2 · (a + b) · hm
Oberfläche
Um die gesamte Oberfläche des Pyramidenstumpfes zu bestimmen, rechnest du die Grundfläche, die Schnittfläche und die Mantelfläche zusammen. Dadurch bekommst du die Pyramidenstumpf Formel
OPyramidenstumpf = G + S + M
OPyramidenstumpf = (a · a) + (b · b) + 2 · (a + b) · hm
Der Pyramidenstumpf ist ein spezieller Typ von Polyedern (Vielfächern). Er entsteht, wenn eine quadratische Ausgangspyramide parallel zu ihrer Grundfläche an den Mantelflächen abgeschnitten wird. Dadurch erhältst du eine kleinere, ähnliche Pyramide (Ergänzungspyramide).
Pyramidenstumpf — häufigste Fragen
(ausklappen)
Pyramidenstumpf — häufigste Fragen
(ausklappen)-
Was ist ein Pyramidenstumpf in einfachen Worten?Ein Pyramidenstumpf ist eine Pyramide, bei der die Spitze abgeschnitten wurde. Unten hat er eine quadratische Grundfläche und oben eine kleinere quadratische Schnittfläche. Die vier Seitenflächen sind gleichschenklige Trapeze und bilden zusammen die Mantelfläche.
-
Was bedeuten a und b beim Pyramidenstumpf?Beim Pyramidenstumpf ist a die Seitenlänge der quadratischen Grundfläche (unten) und b die Seitenlänge der quadratischen Schnittfläche (oben). Damit lassen sich die Flächen berechnen:
 für die Grundfläche und
für die Grundfläche und  für die Schnittfläche.
für die Schnittfläche.
-
Was ist der Unterschied zwischen h und hₘ?h ist die senkrechte Höhe des Pyramidenstumpfs, also der Abstand von der Grundfläche zur Schnittfläche.
 ist die Höhe der Mantelfläche, also die Höhe eines Seiten-Trapezes. Konkret wird
ist die Höhe der Mantelfläche, also die Höhe eines Seiten-Trapezes. Konkret wird  in der Volumenformel verwendet,
in der Volumenformel verwendet,  in der Mantelfläche.
in der Mantelfläche.
-
Wie berechne ich das Volumen von einem Pyramidenstumpf?Das Volumen eines Pyramidenstumpfs berechnest du mit
 . Dabei ist h die senkrechte Höhe, a die Seitenlänge der Grundfläche und b die Seitenlänge der Schnittfläche. Zum Beispiel ergibt sich für a = 8 cm, b = 4 cm und h = 3 cm das Volumen 112 cm³.
. Dabei ist h die senkrechte Höhe, a die Seitenlänge der Grundfläche und b die Seitenlänge der Schnittfläche. Zum Beispiel ergibt sich für a = 8 cm, b = 4 cm und h = 3 cm das Volumen 112 cm³.
-
Wie berechne ich die Oberfläche von einem Pyramidenstumpf?Die Oberfläche eines Pyramidenstumpfs ist die Summe aus Grundfläche, Schnittfläche und Mantelfläche:
 . Dabei gilt
. Dabei gilt  ,
,  und
und  . Die Mantelfläche entsteht, weil vier gleich große Trapeze zusammengezählt werden.
. Die Mantelfläche entsteht, weil vier gleich große Trapeze zusammengezählt werden.
Kegelstumpf
Neben dem Pyramidenstumpf gibt es auch noch den Kegelstumpf . Er sieht aus wie ein Kegel mit abgeschnittener Spitze. Wie du ihn berechnest, zeigen wir dir in unserem Video!