Gleichschenkliges Dreieck
Hier erklären wir dir, was ein gleichschenkliges Dreieck ist und wie du den Flächeninhalt, die Höhe und den Umfang beim gleichschenkligen Dreieck berechnen kannst. Du willst dich beim Lernen lieber zurücklehnen? Dann schau dir einfach unser Video an!
Inhaltsübersicht
Was ist ein gleichschenkliges Dreieck?
Ein gleichschenkliges Dreieck ist ein Dreieck, bei dem zwei Seiten genau gleich lang sind.
Dieses besondere Dreieck hat einige Eigenschaften.
- Die beiden Seiten a (Schenkel) sind gleich lang.
- Die Seite c heißt Basis.
- Die zwei Basiswinkel
 sind gleich groß.
sind gleich groß.
- Die Höhe
 auf der Basisseite c ist eine Symmetrieachse.
auf der Basisseite c ist eine Symmetrieachse. - Die Höhe der Basis
 ist gleichzeitig die Mittelsenkrechte und Seitenhalbierende der Basis c. Außerdem ist diese Linie auch noch die Winkelhalbierende des Winkels gegenüber.
ist gleichzeitig die Mittelsenkrechte und Seitenhalbierende der Basis c. Außerdem ist diese Linie auch noch die Winkelhalbierende des Winkels gegenüber.
Hier findest du zu den wichtigsten Größen im gleichschenkligen Dreieck die Formel zum Berechnen.
Flächeninhalt: 
Umfang: 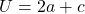
Höhe: 
Die Berechnung im gleichschenkligen Dreieck mit diesen Formeln schauen wir uns jetzt genauer an.
Flächeninhalt gleichschenkliges Dreieck
Der Flächeninhalt im gleichschenkligen Dreieck umfasst alle Punkte, die im Dreieck und auf den Seiten liegen. Für ein gleichschenkliges Dreieck mit Fläche A, brauchst du die Seitenlängen a und c zum berechnen.

Schauen wir uns gleich mal an ein paar Beispielen an, wie du diesen Flächeninhalt eines gleichschenkligen Dreiecks berechnen kannst.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Beispiel 1
Gegeben ist zur Berechnung der Fläche ein gleichschenkliges Dreieck mit zwei Schenkeln  und der Länge der Basis
und der Länge der Basis  . Mit diesen Angaben kannst du den Flächeninhalt im gleichschenkligen Dreieck ganz einfach berechnen.
. Mit diesen Angaben kannst du den Flächeninhalt im gleichschenkligen Dreieck ganz einfach berechnen.
- Formel aufstellen

- Angaben einsetzen

- Ergebnis berechnen

Beispiel 2
Du sollst ein gleichschenkliges Dreieck berechnen, das zwei Schenkel mit Seitenlänge  und eine Seite mit Länge
und eine Seite mit Länge  hat. Gesucht ist der Flächeninhalt.
hat. Gesucht ist der Flächeninhalt.
- Angabe umrechnen

- Formel aufstellen

- Angaben einsetzen

- Ergebnis berechnen

Beispiel 3
Gegeben ist zur Berechnung vom Flächeninhalt ein gleichschenkliges Dreieck mit Seitenlänge  und Höhe
und Höhe  . Hier nutzt du zum Bestimmen die Formel für den Flächeninhalt eines allgemeinen Dreiecks
, weil eine Seite und die dazugehörige Höhe gegeben sind.
. Hier nutzt du zum Bestimmen die Formel für den Flächeninhalt eines allgemeinen Dreiecks
, weil eine Seite und die dazugehörige Höhe gegeben sind.
- Formel aufstellen

- Angaben einsetzen

- Ergebnis berechnen
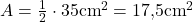
Gleichschenkliges Dreieck Formel Herleitung
Die Formel für den Flächeninhalt im gleichschenkligen Dreieck ergibt sich aus dem Flächeninhalt im allgemeinen Dreieck. Dort gilt
 .
.
Dabei bezeichnet g eine Grundseite des Dreiecks und h die dazugehörige Höhe. Hast du für den Flächeninhalt ein gleichschenkliges Dreieck mit der Basisseite c und der Höhe  , dann ergibt sich
, dann ergibt sich
 .
.
Außerdem gibt es für diese Höhe  im gleichschenkligen Dreieck eine extra Formel, die du später auch nochmal genauer kennenlernen wirst.
im gleichschenkligen Dreieck eine extra Formel, die du später auch nochmal genauer kennenlernen wirst.

Jetzt musst du nur noch diese Höhe in die allgemeine Formel für den Flächeninhalt einfügen und die Gleichung zusammenfassen.

Höhe gleichschenkliges Dreieck
Auch für die Höhe im gleichschenkligen Dreieck gibt es eine extra Formel. Damit kannst du die Höhe  einfach und schnell berechnen.
einfach und schnell berechnen.

Diese Formel für die Höhe im gleichschenkligen Dreieck ergibt sich aus dem Satz des Pythagoras
. Dieser gilt im Dreieck aus einem der Schenkel a, der Hälfte der Basisseite c und der Höhe  .
.

Gleichschenkliges Dreieck c berechnen
Hast du ein gleichschenkliges Dreieck mit Höhe und Schenkel a gegeben, dann kannst du daraus die Basis c berechnen. Sehen wir uns das gleich an einem Beispiel an. Dabei ist die Höhe 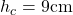 und die Seitenlänge der Schenkel
und die Seitenlänge der Schenkel  .
.
- Formel aufstellen: Zuerst überlegst du dir, welche Formel dir hier weiterhelfen kann. In diesem Fall bietet sich die Formel zur Höhe im gleichschenkligen Dreieck an.

- Nach c auflösen: Um im gleichschenkligen Dreieck c berechnen zu können, löst du die Formel jetzt nach c auf.

- Angaben einsetzen und ausrechnen


So kannst du für ein gleichschenkliges Dreieck Seiten berechnen.
Hinweis: Ein gleichschenkliges Dreieck besitzt Winkel, für die der sogenannte Basiswinkelsatz gilt. Die beiden Winkel an der Basis c sind gleich groß.
Gleichschenkliges Dreieck — häufigste Fragen
(ausklappen)
Gleichschenkliges Dreieck — häufigste Fragen
(ausklappen)-
Wie prüfe ich, ob a und c überhaupt ein Dreieck ergeben?Du prüfst, ob a und c ein Dreieck ergeben, indem du die Dreiecksungleichung anwendest: Die Summe zweier Seiten muss größer als die dritte sein. Beim gleichschenkligen Dreieck gilt daher
 und außerdem
und außerdem  sowie
sowie  .
.
-
Warum teilt die Höhe im gleichschenkligen Dreieck die Basis genau halb?Die Höhe auf die Basis teilt die Basis im gleichschenkligen Dreieck halb, weil das Dreieck eine Symmetrieachse durch die Spitze und den Mittelpunkt der Basis hat. Diese Symmetrie macht die Höhe gleichzeitig zur Seitenhalbierenden (Median) der Basis, daher entstehen zwei gleich lange Basisstücke.
-
Wie berechne ich die Schenkellänge a, wenn c und hc gegeben sind?Du berechnest die Schenkellänge
 , indem du den Satz des Pythagoras im entstehenden rechtwinkligen Teildreieck nutzt:
, indem du den Satz des Pythagoras im entstehenden rechtwinkligen Teildreieck nutzt:  . Daraus folgt
. Daraus folgt  .
.
-
Welche Fehler passieren oft beim Rechnen mit der Wurzel in der Höhenformel?Häufige Fehler bei der Wurzel in
 sind: das
sind: das  fälschlich in die Wurzel zu ziehen und nur
fälschlich in die Wurzel zu ziehen und nur  statt
statt  abzuziehen. Beispiel: Falsch ist
abzuziehen. Beispiel: Falsch ist  , richtig bleibt
, richtig bleibt  .
.
-
Wie unterscheide ich ein gleichschenkliges Dreieck vom gleichseitigen Dreieck?Ein gleichschenkliges Dreieck erkennst du daran, dass genau zwei Seiten gleich lang sind, beim gleichseitigen sind alle drei Seiten gleich lang. Dadurch hat das gleichseitige Dreieck auch drei gleich große Winkel (jeweils
 ), während beim gleichschenkligen nur die beiden Basiswinkel gleich sind.
), während beim gleichschenkligen nur die beiden Basiswinkel gleich sind.
Andere besondere Dreiecke
Jetzt weißt du alles Wichtige über gleichschenklige Dreiecke. Es gibt aber noch andere besondere Dreiecke, zum Beispiel das gleichseitige Dreieck. Schau dir gleich unser Video an, um alles über das gleichseitige Dreieck zu lernen!





