Mantelfläche Zylinder
In diesem Artikel erklären wir dir, was die Mantelfläche vom Zylinder ist und wie du die Zylinder Mantelfläche berechnen kannst. In unserem Video zeigen wir dir den Zylindermantel nochmal anschaulich und mit vielen Beispielen. Schau es dir gleich an!
Inhaltsübersicht
Wie berechnet man die Mantelfläche eines Zylinders?
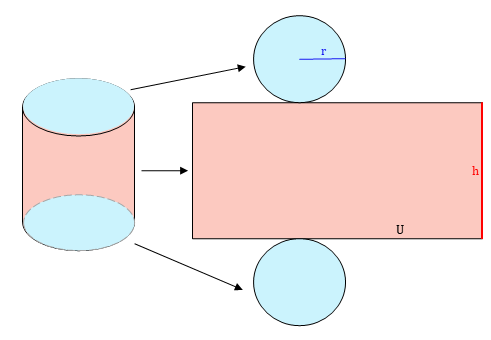
Die Mantelfläche beim Zylinder ist die Fläche, die die beiden blauen Kreise (Deckfläche und Grundfläche) miteinander verbindet. Im Bild ist die Mantelfläche rot eingefärbt.
Der Zylinder Mantel ist damit ein Bestandteil der Oberfläche vom Zylinder. Natürlich gibt es auch eine Formel für die Mantelfläche vom Zylinder.

Um die Zylinder Mantelfläche berechnen zu können, brauchst du also folgende Größen:
- Radius r des Zylinders,
- Höhe h des Zylinders und
- die Kreiszahl
 .
.
Schauen wir uns die Mantelfläche eines Zylinders gleich mal genauer an!
Zylinder Mantelfläche berechnen
Mit der Zylinder Formel für den Mantel vom Zylinder geht das in wenigen Schritten. Gehen wir das an ein paar Beispielen durch.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Herleitung Mantelfläche Zylinder Formel
Mit der Zylinder Formel kannst du die Mantelfläche von jedem Zylinder schnell berechnen. Die Herleitung der Formel ist dabei eigentlich ganz einfach. Dafür stellst du dir einmal vor, dass du den Zylinder Mantel an einer Stelle aufschneidest und abrollst.
So erkennst du, dass die rote Mantelfläche die Form eines Rechtecks hat. Um die Mantelfläche vom Zylinder zu berechnen, musst du also eigentlich nur den Flächeninhalt eines Rechtecks bestimmen. Die entsprechende Formel kennst du schon.

Die Breite des Rechtecks ist genau die Höhe des Zylinders. Die Länge von der Mantelfläche ist ein bisschen komplizierter zu bestimmen. Diese Seite klebt sozusagen an der Grundfläche. Die Grundfläche ist ein Kreis und die Länge der Mantelfläche ist genauso lang wie die Außenlinie dieses Kreises. Sie entspricht dem Umfang vom Zylinder. Um die Länge dieser Außenlinie zu bestimmen, berechnest du den Kreisumfang .

Zum Schluss musst du nur noch die Formel für den Kreisumfang einsetzen. Der Umfang vom Zylinder ist damit ein Teil der Formel. So kommst du zur Formel für die Mantelfläche vom Zylinder.

Insgesamt kannst du dir merken, dass die Mantelfläche aus dem Umfang vom Zylinder mal der Höhe besteht.
Mantelfläche Zylinder — häufigste Fragen
(ausklappen)
Mantelfläche Zylinder — häufigste Fragen
(ausklappen)-
Wie erkenne ich in einer Aufgabe den Radius und nicht den Durchmesser?Du erkennst den Radius daran, dass er die Hälfte des Durchmessers ist und vom Mittelpunkt bis zum Rand reicht. Steht in der Aufgabe „Durchmesser“ oder „d“, ist die ganze Breite gemeint. Zum Beispiel gilt bei
 :
:  .
.
-
Welche Einheit hat eine Mantelfläche?Die Mantelfläche hat am Ende immer eine Flächeneinheit, also zum Beispiel
 ,
,  oder
oder  . Das liegt daran, dass in
. Das liegt daran, dass in  zwei Längen (Radius und Höhe) miteinander multipliziert werden und dadurch „Quadrat-Einheiten“ entstehen.
zwei Längen (Radius und Höhe) miteinander multipliziert werden und dadurch „Quadrat-Einheiten“ entstehen.
-
Wann muss ich bei Radius und Höhe die Einheiten umrechnen?Du musst die Einheiten umrechnen, sobald Radius und Höhe in unterschiedlichen Längeneinheiten angegeben sind, weil die Formel ein einheitliches Maß braucht. Rechne dann eine Größe um, bis beide zueinander passen. Wenn zum Beispiel
 in Metern und
in Metern und  in Zentimetern steht, muss eine der beiden Angaben umgerechnet werden.
in Zentimetern steht, muss eine der beiden Angaben umgerechnet werden.
-
Welche Fehler passieren oft beim Berechnen der Mantelfläche eines Zylinders?Häufige Fehler sind: den Durchmesser statt des Radius einzusetzen, unterschiedliche Einheiten nicht vorher anzugleichen und aus Versehen die Oberfläche statt der Mantelfläche zu berechnen. Bei der Angabe „Durchmesser 10 cm“ muss der Wert 10 cm beispielsweise auf den Radius
 halbiert werden.
halbiert werden.
-
Wie unterscheide ich die Mantelfläche von der Oberfläche eines Zylinders?Du unterscheidest Mantelfläche und Oberfläche daran, dass die Mantelfläche nur die Seitenfläche ist, während die Oberfläche zusätzlich Grundfläche und Deckfläche enthält. Die Mantelfläche berechnet sich mit
 .
.
Oberfläche eines Zylinders
Der Zylindermantel bildet einen Bestandteil der Oberfläche. Damit du die gesamte Oberfläche eines Zylinders berechnen kannst, solltest du dir unbedingt auch noch unser extra Video dazu anschauen!

 und Höhe
und Höhe  gegeben.
gegeben. 


 und Höhe
und Höhe  . Auch hier brauchen wir nur die Formel für die Mantelfläche des Zylinders.
. Auch hier brauchen wir nur die Formel für die Mantelfläche des Zylinders.