Wie erkenne ich in einer Textaufgabe, ob der Radius oder der Durchmesser gemeint ist?

Du erkennst Radius oder Durchmesser an der Beschreibung der Strecke im Kreis: Der Radius ist der Abstand vom Mittelpunkt zur Kreislinie, der Durchmesser geht durch den Mittelpunkt und verbindet zwei Randpunkte. Beispiel: Steht „vom Mittelpunkt bis zum Rand“, ist es der Radius; steht „von Rand zu Rand durch die Mitte“, ist es der Durchmesser.

Welche Fehler passieren oft beim Rechnen mit Pi?

Häufige Fehler beim Rechnen mit sind: zu früh zu runden, doppelt einzusetzen oder zu vergessen und Radius und Durchmesser zu verwechseln. Beispiel: Für den Umfang gilt ; wer fälschlich rechnet, erhält genau die Hälfte des richtigen Umfangs.

Wie rechne ich den Radius aus dem Umfang aus?

Den Radius aus dem Umfang berechnest du, indem du die Umfangsformel nach umstellst: . Das funktioniert, weil der Umfang proportional zum Radius ist; bleibt dabei als Faktor im Nenner.

Wie rechne ich den Durchmesser aus dem Flächeninhalt aus?

Den Durchmesser aus dem Flächeninhalt berechnest du über und : Zuerst , dann . Wichtig ist, dass beim Wurzelziehen die Einheit von Quadrat-Einheit wieder zu einer Längen-Einheit wird.

Warum hat der Flächeninhalt beim Kreis immer eine Quadrat-Einheit?

Der Flächeninhalt hat beim Kreis immer eine Quadrat-Einheit, weil eine Fläche grundsätzlich zweidimensional ist und aus „Länge mal Länge“ entsteht. In der Formel wird der Radius quadriert, also mit sich selbst multipliziert. Deshalb wird aus cm automatisch cm² und aus m automatisch m².

Video

Quiz

Hier geht's zum Video „Umfang Kreis“

Hier geht's zum Video „Flächeninhalt Kreis“

Hier geht's zum Video „Umfang Kreis“

Hier geht's zum Video „Flächeninhalt Kreis“

Kreisberechnung

Wichtige Inhalte in diesem Video

Kreisberechnung einfach erklärt

(00:11)

Durchmesser Kreis berechnen

(01:23)

Radius berechnen

(01:43)

Kreisberechnung Umfang

(01:57)

Kreisberechnung Fläche

(02:39)

In diesem Beitrag geben wir dir eine Übersicht zum Thema Kreisberechnung und zeigen dir die wichtigsten Kreisformeln an ein paar Beispielen. Du willst dich beim Lernen lieber zurücklehnen? Dann schau dir unser Video zu den Kreisberechnungen an! Dort zeigen wir dir jede Kreisformel nochmal Schritt für Schritt.

Inhaltsübersicht

Kreisberechnung einfach erklärt

im Videozur Stelle im Video springen

(00:11)

Bei einem Kreis ist jeder Punkt auf der Kreislinie außen genau gleich weit vom Mittelpunkt M entfernt. Dieser Abstand wird als Radius r bezeichnet und viele andere Formeln der Kreisberechnung bauen auf ihm auf.

Bei der Kreisberechnung kannst du verschiedene Größen am Kreis mit den Kreisformeln bestimmen. Dazu gehört neben dem Radius r und dem Durchmesser d vor allem auch der Umfang U und der Flächeninhalt A des Kreises.

Kreis, Kreisberechnung, Kreisberechnungen, Kreis Formeln — Größen eines Kreises

Für diese Kreisberechnungen musst du dir im Wesentlichen vier Formeln merken.

Kreisberechnung Formeln

Durchmesser: $\textcolor{orange}{d} = 2 \cdot \textcolor{blue}{r}$

Radius: $\textcolor{blue}{r} = \frac{\textcolor{orange}{d}}{2}$

Umfang: $\textcolor{red}{U} = 2 \cdot \textcolor{blue}{r} \cdot \pi$

Fläche: $\textcolor{purple}{A} = \textcolor{blue}{r}^2 \cdot \pi$

Schauen wir uns einmal diese Formeln zur Kreisberechnung genauer an.

Durchmesser Kreis berechnen

im Videozur Stelle im Video springen

(01:23)

Der Durchmesser d in einem Kreis verbindet zwei gegenüberliegende Punkte auf der Kreislinie und geht dabei direkt durch den Mittelpunkt M. Der Durchmesser ist genau doppelt so lang wie der Radius r des Kreises.

$\textcolor{orange}{d} = 2 \cdot \textcolor{blue}{r}$

Du kannst ganz einfach den Durchmesser im Kreis berechnen, wenn du den Radius gegeben hast.

Studyflix vernetzt: Hier ein Video aus einem anderen Bereich

Kreisberechnung Durchmesser Beispiel 1

Berechne den Durchmesser eines Kreises mit Radius $r=3\text{cm}$ .

Formel aufstellen

$d = 2 \cdot r$

Zahlenwert einsetzen

$d = 2 \cdot 3\text{cm}$

Durchmesser ausrechnen

$d = 6\text{cm}$

Kreisberechnung Durchmesser Beispiel 2

Bestimme den Durchmesser im Kreis mit Radius $r=5\text{m}$ .

Formel aufstellen

$d=2 \cdot r$

Zahlenwert einsetzen

$d=2 \cdot 5\text{m}$

Durchmesser ausrechnen

$d=10\text{m}$

Radius berechnen

im Videozur Stelle im Video springen

(01:43)

Die nächste Kreisberechnung ist der Radius eines Kreises. Den Radius r kannst du ganz einfach aus dem gegebenen Durchmesser d berechnen.

$\textcolor{blue}{r} = \frac{\textcolor{orange}{d}}{2}$

Dafür teilst du einfach den Durchmesser durch Zwei.

Kreisberechnung Radius Beispiel 1

Berechne den Radius aus dem Durchmesser $d=8\text{cm}$ .

Formel aufstellen

$r = \frac{d}{2}$

Durchmesser einsetzen

$r=\frac{8\text{cm}}{2}$

Ergebnis ausrechnen

$r=4\text{cm}$

Kreisberechnung Radius Beispiel 2

Bestimme den Radius von einem Kreis mit Durchmesser $d=31\text{mm}$ .

Formel aufstellen

$r=\frac{d}{2}$

Durchmesser einsetzen

$r=\frac{31\text{mm}}{2}$

Ergebnis ausrechnen

$r=15,5\text{mm}$

Kreisberechnung Umfang

im Videozur Stelle im Video springen

(01:57)

Auch der Umfang U spielt bei den Kreisberechnungen eine wichtige Rolle. Diesen kannst du aus dem Radius r oder dem Durchmesser d berechnen.

$\begin{align*} \textcolor{red}{U} &= 2 \cdot \textcolor{blue}{r} \cdot \pi \\ &= \textcolor{orange}{d} \cdot \pi \end{align*}$

Hinweis: Die Kreiszahl $\pi$ ist vermutlich in deinem Taschenrechner eingespeichert. Ansonsten kannst du mit dem gerundeten Wert $\pi \approx 3,14$ rechnen.

Kreisberechnung Umfang Beispiel mit Radius

Berechne den Umfang eines Kreises mit Radius $r=4\text{m}$ .

Kreisformel aufstellen

$U=2 \cdot r \cdot \pi$

Angabe einsetzen

$U=2 \cdot 4\text{m} \cdot \pi$

Ergebnis bestimmen

$U \approx 25,13\text{m}$

Kreisberechnung Umfang Beispiel mit Durchmesser

Bestimme den Umfang aus dem Durchmesser $d=20\text{cm}$ .

Kreisformel aufstellen

$U=d \cdot \pi$

Angabe einsetzen

$U=20\text{cm} \cdot \pi$

Ergebnis bestimmen

$U \approx 62,83\text{cm}$

Mehr Beispiele findest du in unserem extra Video zum Umfang Kreis!

Umfang Kreis, Umfang Kreis berechnen, Kreisumfang, Umfang Kreis formel — Zum Video: Umfang Kreis

Kreisberechnung Fläche

im Videozur Stelle im Video springen

(02:39)

Die letzte der Kreisberechnungen betrifft den Flächeninhalt A. Auch den kannst du mit dem Radius r oder dem Durchmesser d berechnen.

$\begin{align*} \textcolor{purple}{A} &= \textcolor{blue}{r}^2 \cdot \pi \\ &= \frac{\textcolor{orange}{d}^2}{4} \cdot \pi \end{align*}$

Auch für die Kreisberechnung Fläche brauchst du wieder die Kreiszahl $\pi$ . Achte zudem darauf, dass du das Ergebnis mit einer Flächeneinheit wie cm² oder m² angibst.

Kreisberechnung Fläche Beispiel 1

Berechne die Kreisfläche aus dem Radius $r=5\text{cm}$ .

Formel aufstellen

$A = r^2 \cdot \pi$

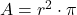
Radius einsetzen

$A = (5\text{cm})^2 \cdot \pi$

Ergebnis ausrechnen

$A = 78,54\text{cm}^2$

Kreisberechnung Fläche Beispiel 2

Bestimme den Flächeninhalt eines Kreises mit Durchmesser $d=24\text{m}$ .

Formel aufstellen

$A = \frac{d^2}{2} \cdot \pi$

Durchmesser einsetzen

$A = \frac{(24\text{m})^2}{4} \cdot \pi$

Ergebnis ausrechnen

$A = \frac{576\text{m}^2}{2} \cdot \pi = 144\text{m}^2 \cdot \pi \approx 452,39\text{m}^2$

Noch mehr Beispiele zum Flächeninhalt Kreis findest du in unserem extra Video!

Flächeninhalt Kreis, Kreis Formel, Flächeninhalt Kreis berechnen — Zum Video: Flächeninhalt Kreis

Kreisberechnungen Beispiele

Mit den Kreis Formeln kannst du auch verschiedene Kreisberechnungen verknüpfen. Das ist vor allem bei etwas komplizierteren Aufgaben wichtig. Hier zeigen wir dir noch einige Beispiele dafür.

Radius berechnen aus Flächeninhalt

Bestimme des Radius r aus dem Flächeninhalt $A=120\text{cm}^2$ .

Kreisformel auflösen

$\begin{align*} A &= r^2 \cdot \pi && | : \pi \\ \frac{A}{\pi} &= r^2 \\ r^2 &= \frac{A}{\pi} && | \sqrt{...} \\ r &= + \sqrt{\frac{A}{\pi}}\end{align*}$

Radius berechnen

$r = +\sqrt{\frac{A}{\pi}} = +\sqrt{\frac{120\text{cm}^2}{\pi}} =+\sqrt{38,97...\text{cm}^2} \approx 6,18 \text{cm}$

Kreisberechnung Flächeninhalt aus Umfang

Berechne den Flächeninhalt A eines Kreises mit Umfang $U=23\text{m}$ .

Radius berechnen

$\begin{align*} U &= 2 \cdot r \cdot \pi && | : \pi \\ \frac{U}{\pi} &= 2 \cdot r && | : 2 \\ \frac{U}{2 \cdot \pi} &= r \\ r &= \frac{U}{2 \cdot \pi} \\ r &= \frac{23\text{m}}{2 \cdot \pi} \\ r &\approx 3,66\text{m} \end{align*}$

Kreisberechnung Fläche

$A = r^2 \cdot \pi = (3,66\text{m})^2 \cdot \pi = 13,39...\text{m}^2 \cdot \pi \approx 42,08\text{m}^2$

Durchmesser Kreis berechnen aus Umfang

Bestimme den Durchmesser eines Kreises mit Umfang $U=64\text{cm}$ .

Kreisformel auflösen

$\begin{align*} U &= d \cdot \pi && | : \pi \\ \frac{U}{\pi} &= d \\ d &= \frac{U}{\pi} \end{align*}$

Durchmesser berechnen

$d=\frac{U}{\pi} = \frac{64\text{cm}}{\pi} \approx 20,37\text{cm}$

Kreisberechnung — häufigste Fragen

(ausklappen)

Wie erkenne ich in einer Textaufgabe, ob der Radius oder der Durchmesser gemeint ist?

Du erkennst Radius oder Durchmesser an der Beschreibung der Strecke im Kreis: Der Radius ist der Abstand vom Mittelpunkt zur Kreislinie, der Durchmesser geht durch den Mittelpunkt und verbindet zwei Randpunkte. Beispiel: Steht „vom Mittelpunkt bis zum Rand“, ist es der Radius; steht „von Rand zu Rand durch die Mitte“, ist es der Durchmesser.
Welche Fehler passieren oft beim Rechnen mit Pi?

Häufige Fehler beim Rechnen mit $\pi$ sind: $\pi$ zu früh zu runden, $\pi$ doppelt einzusetzen oder zu vergessen und Radius und Durchmesser zu verwechseln. Beispiel: Für den Umfang gilt $U = 2 \cdot r \cdot \pi$ ; wer fälschlich $U = r \cdot \pi$ rechnet, erhält genau die Hälfte des richtigen Umfangs.
Wie rechne ich den Radius aus dem Umfang aus?

Den Radius aus dem Umfang berechnest du, indem du die Umfangsformel $U = 2 \cdot r \cdot \pi$ nach umstellst: $r = \frac{U}{2 \cdot \pi}$ . Das funktioniert, weil der Umfang proportional zum Radius ist; $\pi$ bleibt dabei als Faktor im Nenner.
Wie rechne ich den Durchmesser aus dem Flächeninhalt aus?

Den Durchmesser aus dem Flächeninhalt berechnest du über $A = \pi \cdot r^2$ und : Zuerst $r = \sqrt{\frac{A}{\pi}}$ , dann $d = 2 \cdot \sqrt{\frac{A}{\pi}}$ . Wichtig ist, dass beim Wurzelziehen die Einheit von Quadrat-Einheit wieder zu einer Längen-Einheit wird.
Warum hat der Flächeninhalt beim Kreis immer eine Quadrat-Einheit?

Der Flächeninhalt hat beim Kreis immer eine Quadrat-Einheit, weil eine Fläche grundsätzlich zweidimensional ist und aus „Länge mal Länge“ entsteht. In der Formel $A = \pi \cdot r^2$ wird der Radius quadriert, also mit sich selbst multipliziert. Deshalb wird aus cm automatisch cm² und aus m automatisch m².

Flächeninhalt Dreieck

Super! Du weißt nun alle Formeln, die du benötigst um einen Kreis zu berechnen. Damit du alle Aufgaben zur Geometrie problemlos lösen kannst, solltest du auch wissen, wie du ein Dreieck berechnen kannst. Schau dir dazu direkt unser Video zum Flächeninhalt Dreieck an!