Wie erkenne ich in einer Zeichnung die Höhe des Prismas?

Die Höhe eines Prismas ist der Abstand zwischen Grundfläche und Deckfläche, also die Länge der Kanten, die beide Flächen verbinden. In einer Zeichnung ist das meist die „Tiefe“ des Körpers, nicht eine Höhe innerhalb der Grundfläche. Beispiel: Beim Dreiecksprisma ist die Dreieckshöhe nicht die Prismahöhe.

Welche Fehler passieren oft beim Flächeninhalt der Grundfläche?

Häufige Fehler beim Flächeninhalt der Grundfläche sind: die falsche Grundform erkennen, eine Seitenlänge statt der passenden Höhe verwenden und Einheiten beim Flächeninhalt vergessen. Beispiel: Beim Dreieck ist die richtige Höhe die senkrechte Höhe zur gewählten Grundseite, nicht eine schräge Seitenkante.

Wann muss ich bei einem Prisma Einheiten umrechnen?

Einheiten müssen umgerechnet werden, wenn Grundfläche und Prismahöhe in unterschiedlichen Längeneinheiten angegeben sind oder wenn das Ergebnis in einer bestimmten Einheit verlangt ist. Für das Volumen müssen die Längen zusammenpassen, damit in und in cm ein Volumen in ergibt.

Wie unterscheide ich ein Prisma von einer Pyramide?

Ein Prisma erkennst du daran, dass Grundfläche und Deckfläche kongruent (gleich groß und gleich geformt) und parallel sind und die Seitenflächen Parallelogramme (oft Rechtecke) bilden. Eine Pyramide hat nur eine Grundfläche und alle Seitenflächen laufen in einer Spitze zusammen.

Was mache ich, wenn nur die Oberfläche vom Prisma gegeben ist?

Wenn nur die Oberfläche gegeben ist, stellst du die Gleichung auf und nutzt zusätzlich , um Unbekannte zu finden. Ohne weitere Angaben (zum Beispiel eine Kantenlänge, , oder ) lässt sich das Volumen nicht eindeutig bestimmen.

Video

Quiz

Hier geht's zum Video „Flächeninhalt Dreieck“

Hier geht's zum Video „Trapez - Flächeninhalt und Umfang“

Volumen Prisma

Wichtige Inhalte in diesem Video

Wie du das Volumen vom Prisma berechnen kannst, zeigen wir dir hier. Du willst dich beim Lernen lieber zurücklehnen? Dann schau dir jetzt unser Video an!

Inhaltsübersicht

Was ist ein Prisma?

im Videozur Stelle im Video springen

(00:11)

Das Prisma in Mathe ist kein bestimmter geometrischer Körper , sondern eher ein Überbegriff. Prismen haben eine identische Grund- und Deckfläche, die mit Rechtecken verbunden sind. Die Rechtecke bilden zusammen die Mantelfläche.

Prisma, Prismen, Dreiseitiges Prisma, Dreiecksprisma, Prisma Dreieck — Dreiseitiges Prisma

Das Prisma Volumen gibt an, mit wie viel Luft oder Flüssigkeit du den Körper füllen kannst. Die Formel für das Volumen vom Prisma ist:

V = G · h

Häufig ist die Grundfläche vom Prisma ein Dreieck . Es kann aber auch ein Trapez , ein Parallelogramm , ein Fünfeck und so weiter sein. Deshalb gehst du bei der Berechnung des Volumens folgendermaßen vor:

Prisma Volumen berechnen

Berechne die Grundfläche mit der passenden Formel
Setze deine Werte in die Formel ein: Volumen = Grundfläche · Höhe (V = G · h)

Volumen Prisma

im Videozur Stelle im Video springen

(00:29)

Doch wie berechnet man das Volumen eines Prismas jetzt genau? Schau dir an zwei Beispielen die Berechnung des Prisma Volumens an.

Beispiel 1

im Videozur Stelle im Video springen

(00:39)

Zuerst untersuchen wir das Volumen bei einem dreiseitigen Prisma. Seine Grundfläche ist ein Dreieck .

Dreiecksprisma, dreiseitiges Prisma, Prisma mit dreieckiger Grundfläche, Volumen Dreieck, Volumen Prisma — Dreiecksprisma

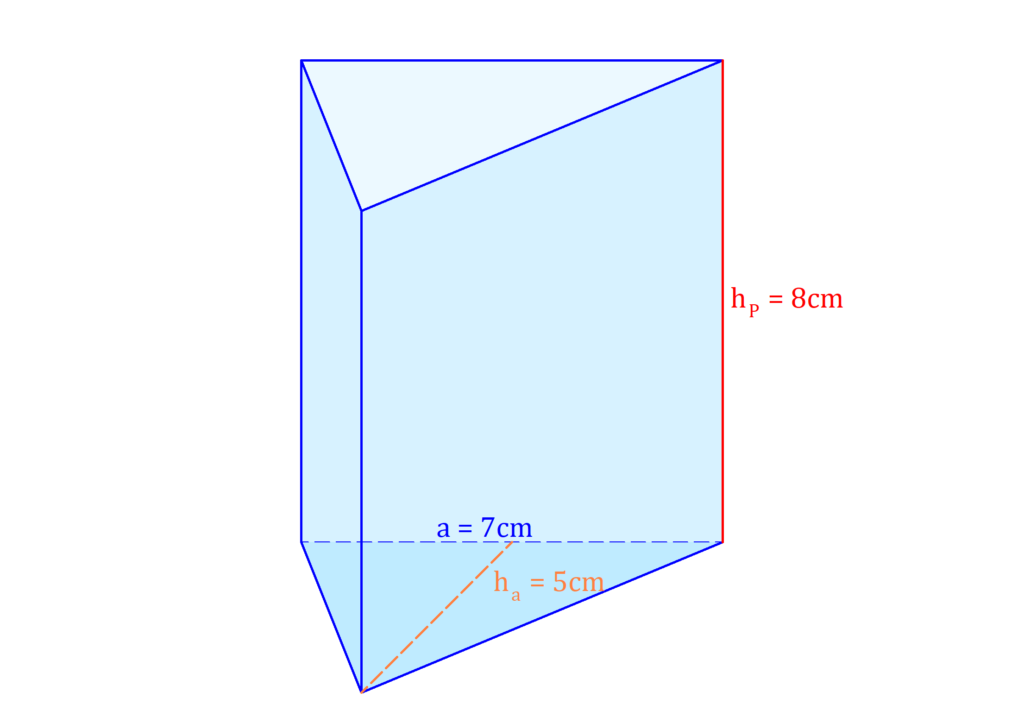
Die allgemeine Formel für das Prisma Volumen lautet V = G · h. Damit kannst du auch das Volumen vom Dreiecksprisma in unserem Beispiel bestimmen. Es ist ein Prisma mit Höhe h_P = 8 cm und einem Dreieck als Grundfläche gegeben. Das Dreieck hat die Seitenlänge a = 7 cm und die dazugehörige Höhe h_a = 5 cm.

1. Grundfläche herausfinden: Zuerst brauchst du für das Volumen die Dreieck Formel für den Flächeninhalt .

G = ½ · a · h_a

2. Grundfläche berechnen: Jetzt kannst du mit den Angaben die Grundfläche bestimmen.

G = ½ · 7 cm · 5 cm = 17,5 cm²

3. Volumenformel aufstellen: Die Grundfläche musst du jetzt nur noch mit der Höhe h_P = 8 cm multiplizieren.

V = G · h_P

4. Ergebnis bestimmen: Zum Schluss setzt du wieder die Angaben ein und kannst das Volumen vom Prisma berechnen.

V = 17,5 cm² · 8 cm = 140 cm³

Insgesamt beträgt das dreiseitige Prisma Volumen V = 140 cm³. Den gleichen Ablauf kannst du für jedes Dreiecksprisma Volumen benutzen.

Beispiel 2

im Videozur Stelle im Video springen

(02:05)

Du kannst aber auch das Volumen von Prismen berechnen, die als Grundfläche kein Dreieck haben. Im zweiten Beispiel ist die Grundfläche vom Prisma ein Trapez . Es heißt deshalb Trapezprisma.

Trapezprisma, Prisma Trapez, vierseitiges Prisma, Trapez Prisma, Prisma vierseitige Grundfläche — Trapezprisma

Schritt für Schritt kannst du auch das Volumen vom Trapez Prisma berechnen. Dafür sind die Seitenlängen a = 5 cm und c = 11 cm, sowie die Höhe der Grundfläche h_T = 6 cm und die Höhe vom Prisma h_P = 7 cm gegeben.

1. Grundfläche herausfinden: Diesmal ist die Grundfläche ein Viereck mit zwei parallelen Seiten a || c. Somit brauchst du für das Volumen die Trapez Formel .

G = ½ · (a + c) · h_T

2. Grundfläche berechnen: Dann kannst du wieder die Zahlenwerte aus der Angabe einsetzen.

G = ½ · (5 cm + 11 cm) · 6 cm = ½ · 16 cm · 6 cm = 48 cm²

3. Volumen Prisma Formel aufstellen: Für die Volumenberechnung vom Prisma kannst du jetzt die allgemeine Formel benutzen.

V = G · h_P

4. Ergebnis bestimmen: Die Höhe entnimmst du wieder der Angabe, um so das Volumen vom Prisma zu berechnen.

V = 48 cm² · 7 cm = 336 cm³

Das Prisma Volumen im Beispiel beträgt insgesamt V = 336 cm³. Um das Volumen eines Prismas zu berechnen, musst du immer zuerst die Grundform erkennen. Deshalb sind die Prisma Formeln so allgemein.

Studyflix vernetzt: Hier ein Video aus einem anderen Bereich

Wie berechnet man die Grundfläche eines Prismas?

Hier geben wir dir nochmal eine Übersicht über die Flächenformeln der verschiedenen Grundformen. Grundsätzlich musst du nur die Figur erkennen und die entsprechende Formel für den Flächeninhalt anwenden, um das Volumen von Prismen zu berechnen.

Abbildung	Grundfläche des Prismas	Formeln
direkt ins Video springen	Allgemeines Dreieck	A = ½ · g · h
direkt ins Video springen	Gleichschenkliges Dreieck	A = ¼ · c · $\sqrt{4\textcolor{blue}{a}^2 - \textcolor{olive}{c}^2}$
direkt ins Video springen	Gleichseitiges Dreieck	A = ¼ · a² · $\sqrt{3}$
direkt ins Video springen	Parallelogramm	A = a · h_a
direkt ins Video springen	Trapez	A = ½ · (a + c) · h

Prisma Formel Zusammenfassung

Da du beim Prisma verschiedene Dinge berechnen kannst, helfen dir die Prisma Formeln:

Prisma Formeln

Volumen Prisma: V = G · h

Oberfläche Prisma: O = 2 · G + M

Mantelfläche Prisma: M = U_G · h

U_G ist der Umfang der Prisma Grundfläche.

Volumen Prisma — häufigste Fragen

(ausklappen)

Wie erkenne ich in einer Zeichnung die Höhe des Prismas?

Die Höhe eines Prismas ist der Abstand zwischen Grundfläche und Deckfläche, also die Länge der Kanten, die beide Flächen verbinden. In einer Zeichnung ist das meist die „Tiefe“ des Körpers, nicht eine Höhe innerhalb der Grundfläche. Beispiel: Beim Dreiecksprisma ist die Dreieckshöhe nicht die Prismahöhe.
Welche Fehler passieren oft beim Flächeninhalt der Grundfläche?

Häufige Fehler beim Flächeninhalt der Grundfläche sind: die falsche Grundform erkennen, eine Seitenlänge statt der passenden Höhe verwenden und Einheiten beim Flächeninhalt vergessen. Beispiel: Beim Dreieck ist die richtige Höhe die senkrechte Höhe zur gewählten Grundseite, nicht eine schräge Seitenkante.
Wann muss ich bei einem Prisma Einheiten umrechnen?

Einheiten müssen umgerechnet werden, wenn Grundfläche und Prismahöhe in unterschiedlichen Längeneinheiten angegeben sind oder wenn das Ergebnis in einer bestimmten Einheit verlangt ist. Für das Volumen müssen die Längen zusammenpassen, damit in $\text{cm}^2$ und in cm ein Volumen in $\text{cm}^3$ ergibt.
Wie unterscheide ich ein Prisma von einer Pyramide?

Ein Prisma erkennst du daran, dass Grundfläche und Deckfläche kongruent (gleich groß und gleich geformt) und parallel sind und die Seitenflächen Parallelogramme (oft Rechtecke) bilden. Eine Pyramide hat nur eine Grundfläche und alle Seitenflächen laufen in einer Spitze zusammen.
Was mache ich, wenn nur die Oberfläche vom Prisma gegeben ist?

Wenn nur die Oberfläche gegeben ist, stellst du die Gleichung $O = 2\cdot G + M$ auf und nutzt zusätzlich $M = U_G \cdot h$ , um Unbekannte zu finden. Ohne weitere Angaben (zum Beispiel eine Kantenlänge, , oder ) lässt sich das Volumen nicht eindeutig bestimmen.

Prisma Oberfläche

im Videozum Video springen

Für die Berechnung des Prisma Volumens hast du nun ein paar Beispiele gesehen. Auch bei der Oberfläche ist die Grundform des Prismas entscheidend! Wie du dabei vorgehst, erfährst du hier!